多层全连接神经网络与情感分析

[LATEXPAGE]

全连接神经网络

全连接神经网络是一种最基本的神经网络结构，英文为Full Connection，所以一般简称FC。FC的准则很简单：神经网络中除输入层之外的每个节点都和上一层的所有节点有连接。

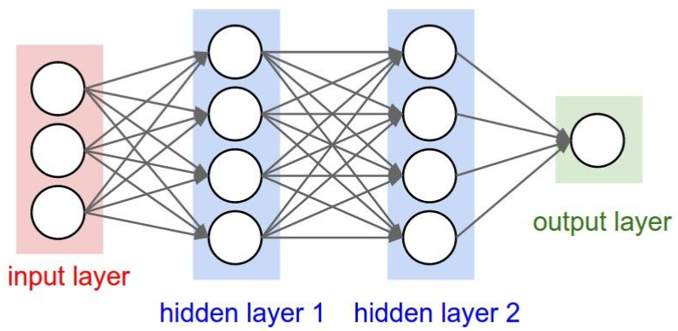
上图是一个双隐层的前馈全连接神经网络，或者叫多层感知机 (MLP)。它的每个隐层都是全连接层。它的每一个单元叫神经元。多层感知机在单层神经网络的基础上引入了一到多个隐藏层（hidden layer）。隐藏层位于输入层和输出层之间。

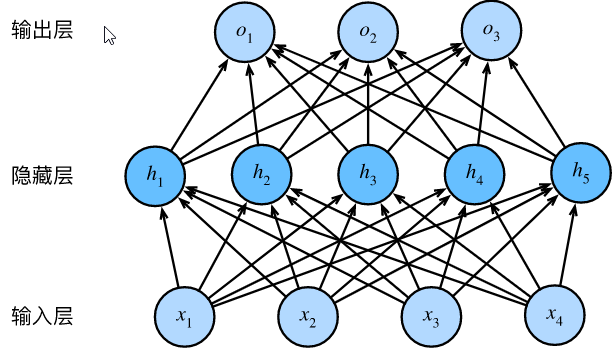
在上图所示的多层感知机中，输入和输出个数分别为4和3，中间的隐藏层中包含了5个隐藏单元（hidden unit）。由于输入层不涉及计算，图中的多层感知机的层数为2。由图可见，隐藏层中的神经元和输入层中各个输入完全连接，输出层中的神经元和隐藏层中的各个神经元也完全连接。因此，多层感知机中的隐藏层和输出层都是全连接层。

具体来说，给定一个小批量样本$\boldsymbol{X} \in \mathbb{R}^{n \times d}$，其批量大小为 n ，输入个数为 d 。假设多层感知机只有一个隐藏层，其中隐藏单元个数为 h 。记隐藏层的输出（也称为隐藏层变量或隐藏变量）为 H ，有$\boldsymbol{H} \in \mathbb{R}^{n \times h}$。因为隐藏层和输出层均是全连接层，可以设隐藏层的权重参数和偏差参数分别为$\boldsymbol{W}_h \in \mathbb{R}^{d \times h}$和$ \boldsymbol{b}_o \in \mathbb{R}^{1 \times q}$，输出层的权重和偏差参数分别为$\boldsymbol{W}_o \in \mathbb{R}^{h \times q}$和$\boldsymbol{b}_o \in \mathbb{R}^{1 \times q}$。

我们先来看一种含单隐藏层的多层感知机的设计。其输出$\boldsymbol{O} \in \mathbb{R}^{n \times q}$的计算为：

$$\boldsymbol{H} = \boldsymbol{X} \boldsymbol{W}_h + \boldsymbol{b}_h,$$

$$\boldsymbol{O} = \boldsymbol{H} \boldsymbol{W}_o + \boldsymbol{b}_o,$$

也就是将隐藏层的输出直接作为输出层的输入。如果将以上两个式子联立起来，可以得到

$$\boldsymbol{O} = (\boldsymbol{X} \boldsymbol{W}_h + \boldsymbol{b}_h)\boldsymbol{W}_o + \boldsymbol{b}_o = \boldsymbol{X} \boldsymbol{W}_h\boldsymbol{W}_o + \boldsymbol{b}_h \boldsymbol{W}_o + \boldsymbol{b}_o.$$

从联立后的式子可以看出，虽然神经网络引入了隐藏层，却依然等价于一个单层神经网络：其中输出层权重参数为 $\boldsymbol{W}_h\boldsymbol{W}_o$，偏差参数为$ \boldsymbol{b}_h \boldsymbol{W}_o + \boldsymbol{b}_o$ 。不难发现，即便再添加更多的隐藏层，以上设计依然只能与仅含输出层的单层神经网络等价。

激活函数

全连接层只是对数据做仿射变换（affine transformation），而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换，例如对隐藏变量使用按元素运算的非线性函数进行变换，然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数（activation function）。下面我们介绍几个常用的激活函数。

ReLU函数

ReLU（rectified linear unit）函数提供了一个很简单的非线性变换。给定元素 x ，该函数定义为：$\text{ReLU}(x) = \max(x, 0).$

可以看出，ReLU函数只保留正数元素，并将负数元素清零。

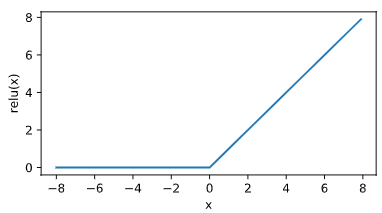
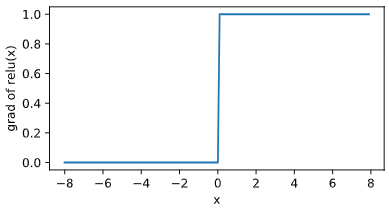
显然，当输入为负数时，ReLU函数的导数为0；当输入为正数时，ReLU函数的导数为1。尽管输入为0时ReLU函数不可导，但是我们可以取此处的导数为0。

sigmoid函数

sigmoid函数可以将元素的值变换到0和1之间：$\text{sigmoid}(x) = \frac{1}{1 + \exp(-x)}.$

sigmoid函数在早期的神经网络中较为普遍，但它目前逐渐被更简单的ReLU函数取代。下面绘制了sigmoid函数。当输入接近0时，sigmoid函数接近线性变换。

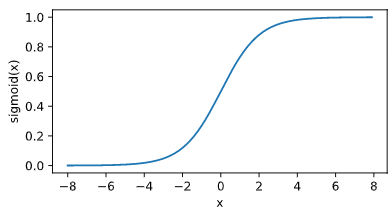
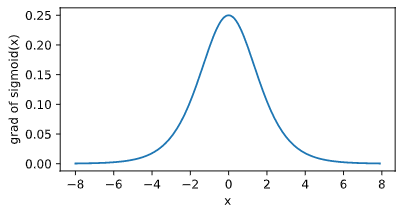
依据链式法则，sigmoid函数的导数：$\text{sigmoid}'(x) = \text{sigmoid}(x)\left(1-\text{sigmoid}(x)\right).$

当输入为0时，sigmoid函数的导数达到最大值0.25；当输入越偏离0时，sigmoid函数的导数越接近0。

tanh函数

tanh（双曲正切）函数可以将元素的值变换到-1和1之间：$\text{tanh}(x) = \frac{1 – \exp(-2x)}{1 + \exp(-2x)}.$

当输入接近0时，tanh函数接近线性变换。虽然该函数的形状和sigmoid函数的形状很像，但tanh函数在坐标系的原点上对称。

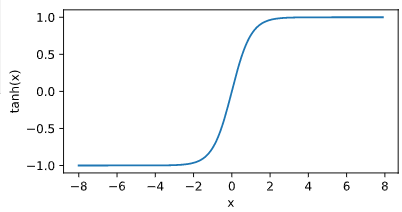
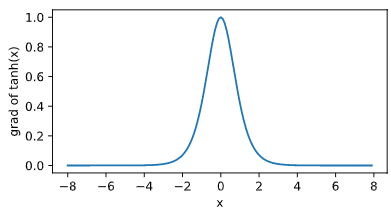
依据链式法则，tanh函数的导数：$\text{tanh}'(x) = 1 – \text{tanh}^2(x).$

当输入为0时，tanh函数的导数达到最大值1；当输入越偏离0时，tanh函数的导数越接近0。

全连接网络的实现

线性回归

给定由 d 个属性描述的实例 $x = (x_1; x_2;…; x_d)$，线性模型试图学习一个通过属性的线性组合来预测的函数，即：$f(x) = \sum_{i=1}^d w_i x_i + b$。写成向量表示即：$f(x) = \mathbf{w^T} \mathbf{x} + b$。

那我们如何衡量f(x)与y之间的差别呢？在回归任务中，我们最常采用均方误差来度量，即：$loss = \sum_{i=1}^n (f(x_i) – y)^2$。要使 loss 最小，我们可以分别对w和b求偏导数，令其为0，得到解析解：

$$w = \frac{\sum_{i=1}^m y_i(x_i – \overline{x})}{\sum_{i=1}^m x_i^2 – \frac{1}{m} (\sum_{i=1}^m x_i)^2}$$

$$b = \frac{1}{m} \sum_{i=1}^m (y_i – w x_i)^2$$

若$\mathbf{X^TX}$满秩，可写成向量形式：$\mathbf{\hat{w}^*} = \mathbf{(X^T X)^{-1} X^T y}$

感知机

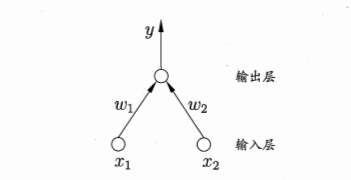
这是一个两输入神经元的感知机网络结构示意图，上文提到，单神经元感知机做了一个线性运算，再把结果输入激活函数，即$y = f(\sum_{i=1}^n w_i x_i + b)$，f即为激活函数。但是单层感知机学习能力非常有限，无法解决线性不可分问题，如异或问题。这时我们就需要多层感知机。感知机隐层越多，理论上就能拟合越复杂的函数。

多层感知机 (Multilayer Perceptron, MLP)

我们说 MLP 是全连接神经网络，因为它的每一个神经元把前一层所有神经元的输出作为输入，其输出又会给下一层的每一个神经元作为输入，相邻层的每个神经元都有“连接权”。神经网络学到的东西，就蕴含在连接权和阈值（偏置）中。

由于引入了非线性的激活函数，感知机通常无法求得解析解，在深度神经网络中，损失函数通常是非凸的，所以只能求得数值解，而梯度下降法是最常用的方法。

反向传播 (Back Propagation, BP)

我们训练神经网络的目标，就是优化损失函数使其达到最小。不同的任务通常使用不同的损失函数。通常使用反向传播算法来训练神经网络。下面以单隐层感知机为例，说明反向传播算法是如何工作的。假设每层神经元都用 Sigmoid 函数作为激活函数，并且使用均方误差函数作为损失函数。

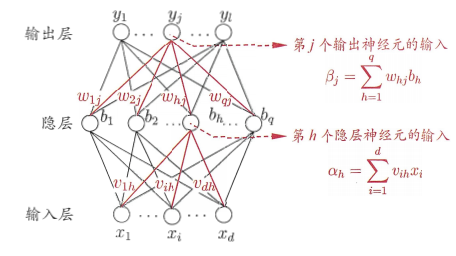
对训练例$(x_k, y_k)$，设神经网络输出为$\mathbf{\hat{y}_k} = (\hat{y}_1^k, \hat{y}_2^k, …, \hat{y}_l^k)$，即：$\hat{y}_j^k = f(\beta_j – \theta_j)$，均方误差：$E_k = \frac{1}{2} \sum_{j=1}^l (\hat{y}_j^k – y_j^k)^2$。BP 是一个迭代学习算法，基于梯度下降策略，任意参数v的更新估计式为：$v \leftarrow v + \Delta v$。

我们以$w_{hj}$进行推导，给定学习速率$\eta$，有：$\Delta w_{hj} = -\eta \frac{\partial E_k}{\partial w_{hj}}$。由链式规则：$\frac{\partial E_k}{\partial w_{hj}} = \frac{\partial E_k}{\partial \hat{y}_j^k} \cdot \frac{\partial \hat{y}_j^k}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial w_{hj}}$

对于 Sigmoid 函数：

$$f’(x) = f(x)(1 – f(x))$$

$$\begin{split} g_j &= -\frac{\partial E_k}{\partial \hat{y}_j^k} \cdot \frac{\partial \hat{y}_j^k}{\partial \beta_j}\ &= -(\hat{y}_j^k – y_j^k)f’(\beta_j – \theta_j) \ &= \hat{y}_j^k (1 – \hat{y}_j^k)(y_j^k – \hat{y}_j^k)\end{split}$$

$$\Delta w_{hj} = \eta g_j b_h$$

对于其他参数，我们也采用一样的方法求得偏导数。但是上述过程比较复杂，实际上在神经网络模型中，我们采用计算图模型来实现自动求导。

计算图

以$f(w,x) = \frac{1}{1 + e^{-(w_0 x_0 + w_1 x_1 + w_2)}}$为例，演示计算图是怎么计算导数的。

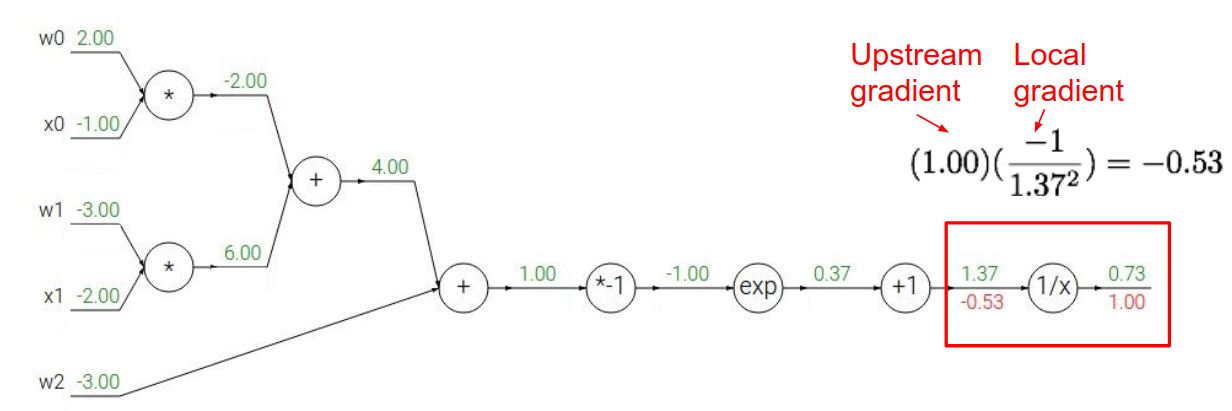
简单来说，要点就是链式规则。对一个节点n来说，它的输入为$x_n$，输出为$y_n$，损失函数为L，有$\frac{\partial L}{\partial x_n} = \frac{\partial L}{\partial y_n} \cdot \frac{\partial y_n}{\partial x_n}$，即 UpstreamGradient * LocalGradient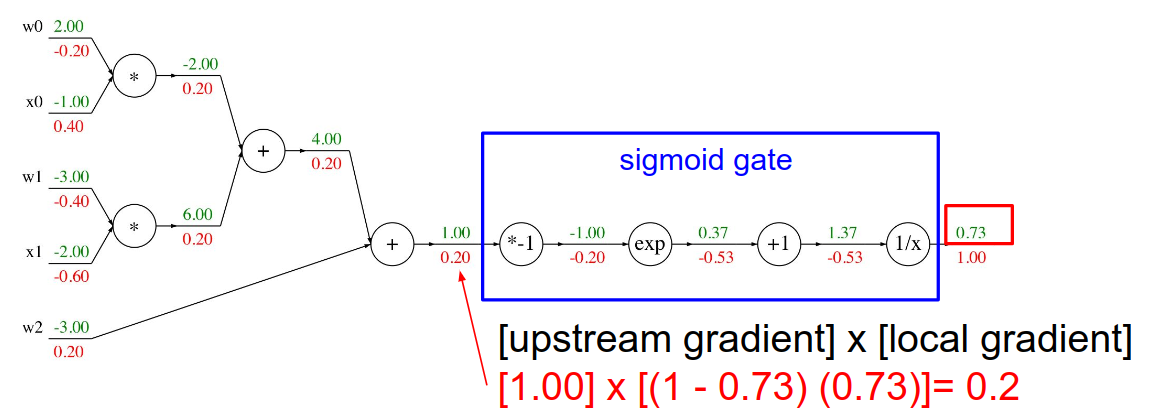

当然，我们可以把一个函数运算当做计算图的一个 Operation，即把函数运算涉及到的节点合并成一个节点。如 Sigmoid 的导数：$\sigma’(x) = \sigma(x) (1 – \sigma(x))$，计算过程如上图。

全连接层的作用

全连接的核心操作是矩阵乘法，本质上是把一个特征空间线性变换到另一个特征空间。实践中通常是把特征工程（或神经网络）提取到的特征空间映射到样本标记空间，参数w相当于做了特征加权。由于这个特性，在 CNN 中，FC 常用作分类器，即在卷积、池化层后加 FC 把特征变换到样本空间。而卷积可以看做一定条件约束的“全连接”，如用 1 * 1 的卷积，可以与全连接达到同样的效果。但是由于全连接层参数冗余，有些模型使用全局平均池化 (Global Average Pooling, GAP) 来代替全连接。不过在迁移学习中， FC 可充当“防火墙”，不含 FC 的网络微调后效果比含 FC 的差。特别在目标域和源域差别比较大的，FC 可保证模型表示能力的迁移。

多层全连接神经网络训练情感分析

Keras 自带的imdb情感数据

Keras 自带了imdb 的数据和调取数据的函数，直接调用load.data()就可以了。

import numpy as np
from keras.datasets import imdb
import matplotlib.pyplot as plt

(X_train, y_train), (X_test, y_test) = imdb.load_data()  # load_data函数从亚马逊S3 中下载数据
print(X_train[0])  # 每个词标注了一个索引(index)，创建了字典。每段文字的每个词对应了一个数字。
print(y_train[:10])  # y 就是标注，1 表示正面，0 表示负面。
print(X_train.shape)
print(y_train.shape)
avg_len = list(map(len, X_train))
print(np.mean(avg_len))
print(max(list(map(len, X_train))))
print(max(list(map(len, X_test))))

plt.hist(avg_len, bins=range(min(avg_len), max(avg_len) + 50, 50))
plt.show()

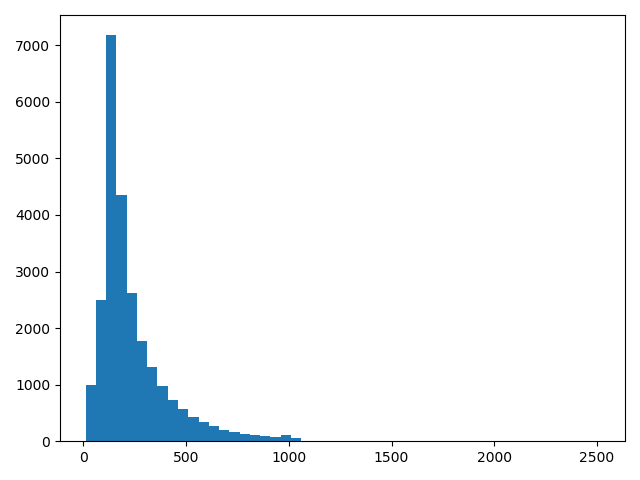
可以看到平均字长为238.71364。为了直观显示，这里画一个分布图：

Keras 提供了设计嵌入层（Embedding Layer）的模板。只要在建模的时候加一行Embedding Layer 函数的代码就可以。注意，嵌入层一般是需要通过数据学习的，也可以借用已经训练好的嵌入层比如Word2Vec 中预训练好的词向量直接放入模型，或者把预训练好的词向量作为嵌入层初始值，进行再训练。

Embedding 函数定义了嵌入层的框架，其一般有3 个变量：字典的长度（即文本中有多少词向量）、词向量的维度和每个文本输入的长度。注意，每个文本可长可短，所以可以采用Padding 技术取最长的文本长度作为文本的输入长度，而不足长度的都用空格填满，即把空格当成一个特殊字符处理。空格本身一般也会被赋予词向量，这可以通过机器学习训练出来。Keras 提供了sequence.pad_sequences 函数帮我们做文本的处理和填充工作。

最长的文本有2494 个字符，考虑到文本的平均长度为230 个字符，可以设定最多输入的文本长度为400 个字符，不足400 个字符的文本用空格填充，超过400 个字符的文本截取400 个字符，Keras 默认截取后400 个字符。

from keras.models import Sequential
from keras.layers import Dense, Flatten
from keras.layers.embeddings import Embedding
from keras.preprocessing import sequence
import numpy as np
from keras.datasets import imdb

(X_train, y_train), (X_test, y_test) = imdb.load_data()

max_word = 400
X_train = sequence.pad_sequences(X_train, maxlen=max_word)
X_test = sequence.pad_sequences(X_test, maxlen=max_word)
vocab_size = np.max([np.max(X_train[i]) for i in range(X_train.shape[0])]) + 1

model = Sequential()
model.add(Embedding(vocab_size, 64, input_length=max_word))
model.add(Flatten())
model.add(Dense(2000, activation='relu'))
model.add(Dense(500, activation='relu'))
model.add(Dense(200, activation='relu'))
model.add(Dense(50, activation='relu'))
model.add(Dense(1, activation='sigmoid'))

model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())

model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=20, batch_size=100, verbose=1)
score = model.evaluate(X_test, y_test)
print(score)

整个模型的结构如下：

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_1 (Embedding)      (None, 400, 64)           5669568   
_________________________________________________________________
flatten_1 (Flatten)          (None, 25600)             0         
_________________________________________________________________
dense_1 (Dense)              (None, 2000)              51202000  
_________________________________________________________________
dense_2 (Dense)              (None, 500)               1000500   
_________________________________________________________________
dense_3 (Dense)              (None, 200)               100200    
_________________________________________________________________
dense_4 (Dense)              (None, 50)                10050     
_________________________________________________________________
dense_5 (Dense)              (None, 1)                 51        
=================================================================
Total params: 57,982,369
Trainable params: 57,982,369
Non-trainable params: 0
_________________________________________________________________

模型结构：

• 第一层是嵌入层，定义了嵌入层的矩阵为vocab_size 64。每个训练段落为其中的max_word 64矩阵，作为数据的输入，填入输入层。
• 然后把输入层压平，原来是max_word * 64 的矩阵，现在变成一维的长度为max_word * 64的向量。
• 接下来不断搭建全连接神经网络，使用relu 函数。
• 最后一层用Sigmoid，预测0，1 变量的概率，类似于logistic regression 的链接函数，目的是把线性变成非线性，并把目标值控制在0~1。因此这里计算的是最后输出的是0 或者1 的概率。

交叉熵（Cross Entropy）

交叉熵主要是衡量预测的0，1 概率分布和实际的0，1 值是不是匹配，交叉熵越小，说明匹配得越准确，模型精度越高。

其具体形式为：$y \log(\hat{y})+(1-y)\log(1-\hat{y})$

这里把交叉熵作为目标函数。我们的目的是选择合适的模型，使这个目标函数在未知数据集上的平均值越低越好。所以，我们要看的是模型在测试数据上的表现。

Adam Optimizer

Adam Optimizer 是一种优化办法，目的是在模型训练中使用的梯度下降方法中，合理地动态选择学习速度（Learning Rate），也就是每步梯度下降的幅度。直观地说，如果在训练中损失函数接近最小值了，则每步梯度下降幅度自然需要减小，而如果损失函数的曲线还很陡，则下降幅度可以稍大一些。从优化的角度讲，深度学习网络还有其他一些梯度下降优化方法，比如Adagrad 等。它们的本质都是解决在调整神经网络模型过程中如何控制学习速度的问题。

全连接神经网络几乎对网络模型没有任何限制，但缺点是过度拟合，即拟合了过多噪声。全连接神经网络模型的特点是灵活、参数多。在实际应用中，我们可能会对模型加上一些限制，使其适合数据的特点。并且由于模型的限制，其参数会大幅减少。这降低了模型的复杂度，模型的普适性进而会提高。接下来我们介绍卷积神经网络（CNN）在自然语言的典型应用。