分层时间记忆算法(Hierarchical Temporal Memory),全称HTM Cortical Learning Algorithms是由Numenta公司发表的新一代人工智能算法。HTM算法旨在模拟新大脑皮层的工作原理,将复杂的问题转化为模式匹配与预测。正如它的名字HTM一样,该算法与普通的神经网络算法有诸多的不同之处。HTM强调对“神经元”进行分层级,强调信息模式的空间特性与时间特性。目前Numenta公司已经推出基于HTM算法的Python平台和可进行视觉识别的软件工具箱。
HTM简介
HTM是一种通用人工智慧(或称强人工智慧)的模型。这个模型的背后是基于对脑神经科学的了解、结合数学与电脑科学理论、最终组合起来的一种学习方法,是一种对人类大脑学习能力的模仿。即使最初的想法跟神经网路有些相似之处,但在后来的发展与实作的细节上,走的是另一条完全不一样的路。
传统的人工智能算法大多是针对特定的任务目标而设计的。HTM算法与之不同,它注重先把问题转化成模式匹配与预测的问题再解决。这使提出人工智能的“统一理论”成为可能。HTM算法是建立在大量解剖学和神经科学的基础上的。HTM算法认为人类之所以具有智能,新大脑皮层是不可缺少的必要条件,并且由其承担高级脑活动。我们的大脑的运行机制是将接受到的各种模式与记忆中模式进行匹配,并对下一刻将会接收到的信息作出预测及反应,如此循环往复。这正是其时效性(Temporal)的体现。
HTM算法表面上与神经网络算法有相似之处,其实质是完全不同的。这就好比一般电路与门电路的区别。将模拟“神经元”按照新大脑皮层的结构连接之后就会产生与一般神经网路完全不同的效果。一般的神经网络注重前馈,而HTM算法更注重信息的双向交流,这也是由于神经解剖学发现反馈突触数量不亚于前馈的原因。而反馈并不能得到大多数人的重视。
HTM算法也是一种拥有记忆性和可学习性的算法。它相对于其他学习算法更注重对神经网络的训练而不是架构。HTM算法认为只要经过合理的训练,该算法适用于解决大多数人工智能问题。对于不同的任务目标实验者需要将数据先空间化和时间化再对HTM网络进行训练即可。
HTM包含新大脑皮质的三个显著特性:
- 记忆系统。数据流通过感观进入大脑皮质,其中的神元细胞通建立突触(snapses)连接,达到学习的目的,并将记忆储存其中。每个神经元都可看成一个“记忆”系统。
- 记忆主要为时间(time-changing/temporal)模式。数据在新皮质上的输入输出是实时动态的,而且皮质的对输入数据的学习也是基于时间的,并基于此对动态信息进行预判。
- 层级连接。新皮质内的神经元在皮质内是以层级的方式连接的。因为所有的神经元都执行同样的基本记忆操作,故理解一个神经元的工作方式,即可理解整个皮质的工作方式。
HTM模型相对于现行类神经网路模型的优势:
- 持续学习/在线学习。类神经网路分类器一般在训练完毕、内部权重确定之后,就会切换为predition mode开始正式上线服役。但在现实世界中,新的资料仍会持续形成新的pattern。所以类神经网路模型通常会需要在上线一段时间之后,下线用新的资料重新训练。如何让类神经网路模型能够在服役同时仍保有学习能力,一直仍是大家各说各话,没有统一的最佳答案。HTM则号称能原生保有这样的能力。
- 噪声鲁棒性和容错性。我们目前知道,类神经网路对于输入资料的细微扰动非常敏感。分类错误的资料、遗失的资料、或刻意变造的资料都可以相当大程度的干扰类神经网路的训练与预测能力。如何在类神经网路中增强抵抗杂讯干扰的能力依然是个研究中的问题。但HTM号称有原生的抗噪能力。
- 没有超参数调整。基于类神经网路模型的人工智慧一直被人嘲笑为「炼丹」、机器学习工程师自嘲是「链金术士」或「炼丹师」,就是因为在训练类神经网路模型的过程中有太多的hyperparameter需要决定,但该怎么决定却几乎都凭经验跟运气,甚至有「收敛看运气,效果看天命」的说法。没有一个有系统的、有数学理论支撑的决定方式。最简单的例子,光是Learning rate要怎么调,就有一大堆的paper。光是网路的架构要怎么设定(要几层?用什么层?太少层精确度不高,太多层又会梯度消失直接在训练阶段爆炸)就可以搞死人。即使后来有NAS与自动语言的帮忙,「调参」依然是一个大麻烦。如果HTM完全不需要调参(或只有很少的参数要决定),那真的会是一大优势。
成功应用HTM的关键在于把它用于一个适合HTM的问题并对该问题进行恰如其分的阐述。HTM并不适于解决可以用一组离散的规则就能解决的问题。HTM最适合于这样的问题:用于建模的数据是从时变(随时间变化的)causes的层次结构中产生的。这里的一个cause是指一个产生HTM输入数据的目标(好像可以理解为因果关系的“因”)。这个问题必须同时包含空间和时间成分。总而言之,HTM所应用的领域需要有一个内在的层次结构,并且数据必须有时间和空间的关联。同时还要有以时间序组织起来的充分数据以供训练。
千脑智力理论
Thousand Brain Theory发想自脑神经科学领域对于人类大脑的研究。
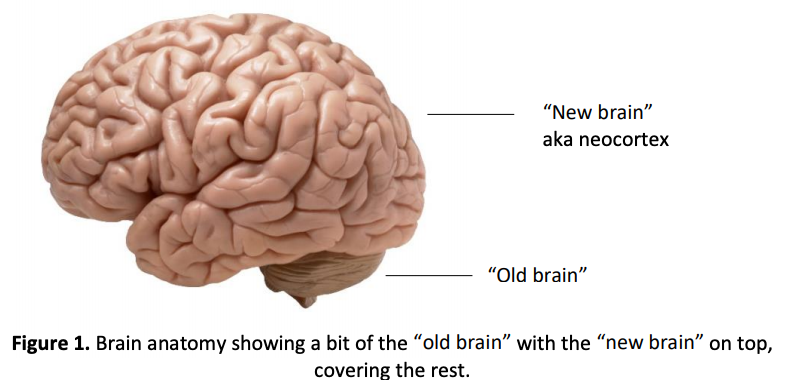
图片中的“New Brain”是人类掌管高阶行为(如感知物体与学习能力)的地方。而在Neocortex(新皮质)中,充满了柱状结构的细胞,长得如下图:

这些柱状结构的细胞称为Cortical Columns,负责处理来自各个感官的刺激讯号:某些区域的Cortical Columns连接到眼睛,该区域就负责处理视觉信号;若是连接到耳朵,就负责处理听觉信号等等。
而这些感官来的刺激信号,会伴随着感官所在的绝对位置信号、以及物体与感官的相对位置信号(由名为Grid Cells的细胞产生),一起被处理。
根据这样的生理结构,Jeff等人提出了一个假说:每一个Cortical Column都能透过感官传来的讯号以及感官所在的位置讯号,平行感知并学习一个物体模型。而最终人类所感知到的物体模型则是由数以千计的Cortical Column共同随时间组合起来的。
这个核心概念与类神经网路(Artificial Neural Networks)的设计想法不太一样:类神经网路中,每个输入节点(Neuron)只负责学习一个模型的一小部分,最前面的层(Layer)学习基础的特征(如直线、斜线等),越后面的层则会学习较高阶的特征(如形状、轮廓等等),并要到最后一层,才能根据这些高阶特征来决定是什么物体。
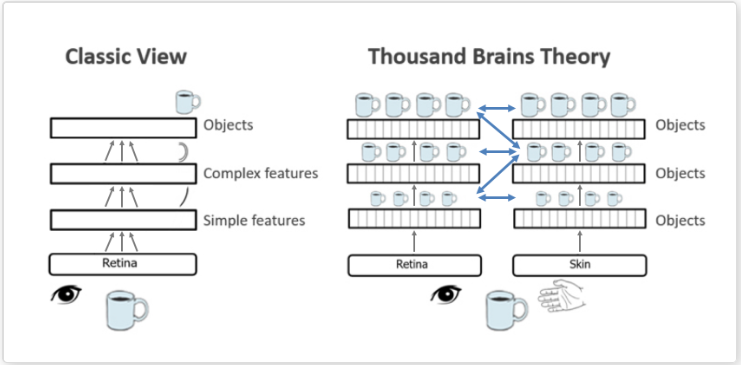
Jeff等人对现行的类神经网路,提出一个重要的质疑:类神经网路需要许多层以及大量已知的训练资料才能学习某些简单的任务,如辨认一个咖啡杯。但人类不需要看过千万张咖啡杯的照片才能学会什么是咖啡杯。
论文中举出一个蛮极端的例子:学习只用一根手指,用摸的方式辨认咖啡杯。在这个例子中,人脑的学习流程是(如下图右):
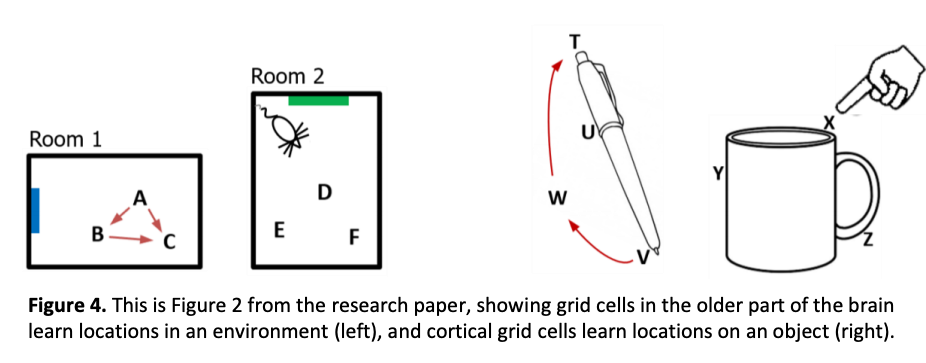
- 手指首先触碰到x点,学习到手指的触觉信号(杯口的感觉)与手指所在的位置(杯子上缘)。
- 下一个时间点,手指移动到y点,同样学习到手指在y点的触觉(杯子的本体)以及手指在y点的位置(杯子左侧)。
- 再下一个时间点,手指移动到z点,再次学习触觉信号(把手)以及位置讯号(杯子另一侧)
- 根据以上三点,建立物件的轮廓(有圆圆的上缘、平直的一侧、有圆弧提把的另一侧等等),并以这个轮廓作为特征。
- 下次手指碰触到同样的感觉序列的时候,人脑就知道这是个杯子。
而以上的学习方法,都需要 Cortical Columns 与 cortical grid cells 产生的感觉讯号以及位置讯号共同实现。论文提到这种利用位置的时间变异来记忆并学习的方式,正是人类古老演化而来的、在大自然环境中记忆环境以及找出回家的路的方式。同样的方法在近代也被采用来作为增强学习的方式之一。
在学完基本的物体之后,我们接着讨论,人脑是如何学习更复杂的物件(如复合物件)的特征的?一个简单好懂的例子:以视觉来学习什么是车子:
- 学习轮子看来的样子(习得:轮子)。
- 学习窗户看起来的样子(习得:窗户)。
- 学习引擎盖看起来的样子(习得:引擎盖)。
- 学习车子看起来的样子(习得:车子=轮子+窗户+引擎盖)。
- 下次看到卡车,因为卡车也有同样的特征(轮子+窗户+引擎盖),故得知卡车也是一种车子,不用另外学习。
这种复杂物件的特征可以用简单物件的特征组合起来的特性:我们所知道的几乎所有事物都是由我们已经学过的其他事物组成的,这使大脑能够高效地学习新事物,而不必不断地从头开始学习一切。
另一种学习方式是以物体的行为模式(Object Behaviors)作为学习目标。以下图的钉书机为例子:
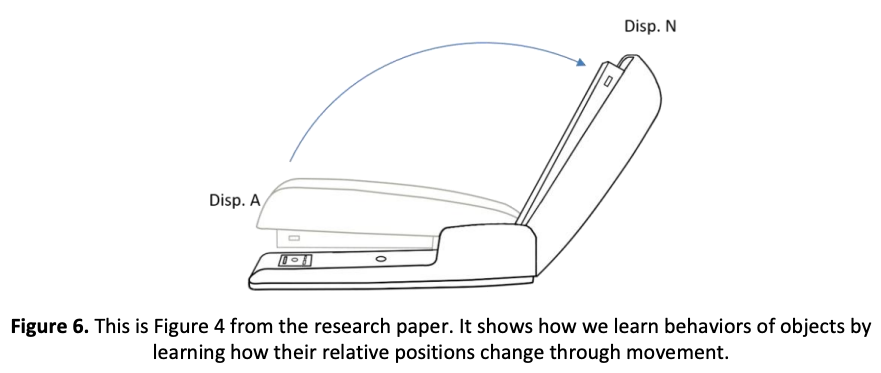
- 学习物体在 A 位置的样子
- 学习物体随着时间移动到 N 的样子
- 下次看到有一个物体有同样子的相对位置随时间变化的序列(钉书机打开—闭合的序列)时,就说拥有这种「行为」的物体是钉书机。
- 下次遇到一个被称为是「钉书机」的物体时,也会预期这个物体会展现同样的行为(打开—闭合)。
对象是作为一组位置来学习的,学习行为就是学习一系列的位移。换句话说,我们学习行为,作为两个位置的相对位置如何随时间变化的顺序(在这种情况下,是订书机的顶部和底部)。
Thousand Brain Theory of Intelligence 理论的总整理:
- 千脑智能理论 – 因为每个皮质柱都可以学习完整的对象模型,所以大脑会同时创建数千个模型,而不是一个大模型。
- 位置,位置,位置 – 每个皮层柱都有一个位置信号,我们建议通过皮层网格单元来实现。
- 对象组成 – 我们提出了一种遍布大脑的新型神经元,即“置换细胞”,它们使我们能够了解对象是如何由其他对象组成的。
- 对象的行为 – 了解对象的行为只是简单地了解位移单元跟踪的运动顺序。
- 概念和高级思考 – 我们以学习物理对象的方式学习概念性想法。
在过往训练类神经网路的经验中,很基础的一个观念就是:一个类神经网路在训练完成之后,就只能专注做一件事,也就是它被训练来要做的事。一个被训练来分辨 MNIST 的类神经网路不管准确度再高,一旦丢给它一个根本不属于 MNIST 资料集范畴内的图片,整个分类器系统就可能直接崩溃什么都给不出来。更不要提针对性的细微扰动,可以蓄意的破坏一个类神经网路分类器执行任务的能力。
相对于传统类神经网路所建立的专家系统,Thousand Brain Theory of Intelligence 描绘的 AI 更接近于强人工智慧或称通用人工智慧(Artificial General Intelligence)。只要学得事物的基础架构,并结构化、阶层化的累积所学到的东西,对于未知的新任务就可以不用特意重新训练,而将现有的模型直接转移使用,并持续在新任务中学习新的 pattern。
具有皮质学习算法的 HTM
HTM 的层级结构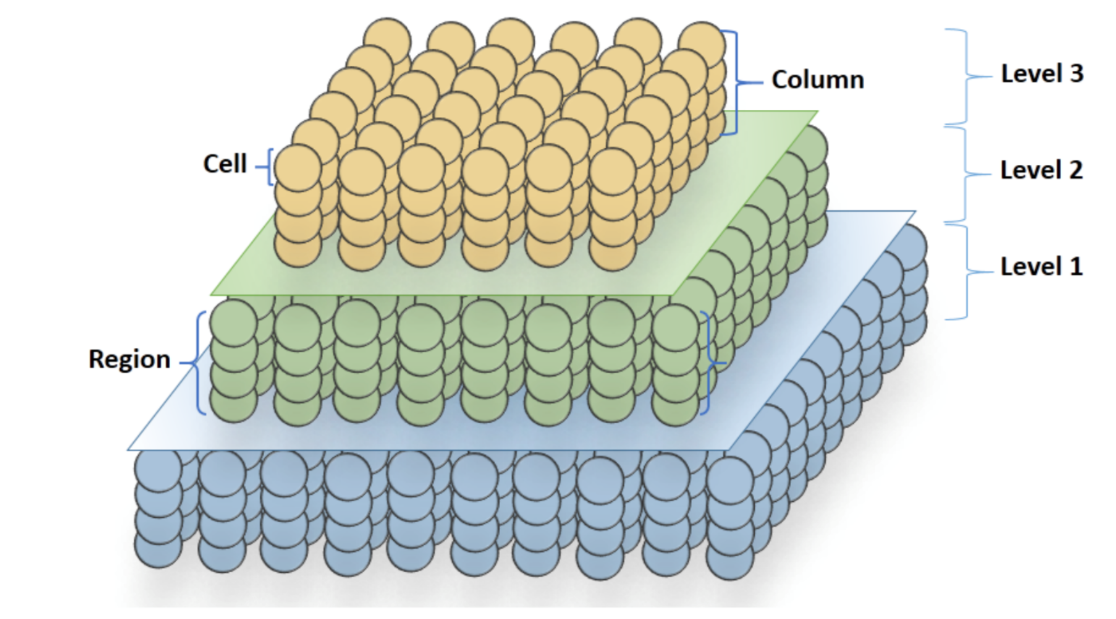
上图表现的即为简化在脑皮质结构,也是 HTM 和大致结构。HTM 是层级结构。在每一层中,都有大量单元(cell),多个单元组成单元柱(mini-column),多个单元柱组成区块(region)。
我们考虑一层的皮质时,我们可以将其看成是为二维点阵列(每个点是一个单元,每一列是一个单元柱)。

HTM 是多层的树状结构,感知器感知到的信号先输入到底层的节点,节点的输出(Beliefs)再层层传递到最高层。如下图:
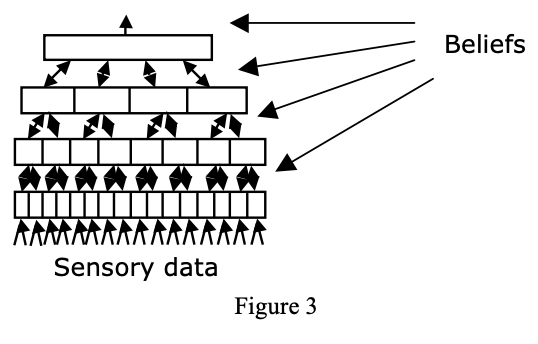
图中的所谓 Belief 为 Cause 的机率阵列,如下图:
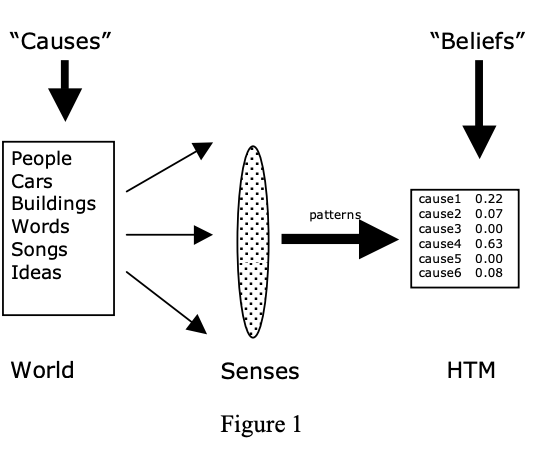
在 Thousand Brain Theory 中提到过,每个节点(Column)都会学习到完整的世界观。但底层的节点只会学到最简单的物件,而越往上层的节点则会学到越复杂的复合物件。这也意味着,HTM 所需的层数与所需辨识的物件的复杂度呈正相关。
在层次结构的最低级别,您的大脑存储有关视野的微小部分(例如边缘和拐角)的信息。边缘是世界上许多对象的基本组成部分。这些低级样式在中级被重组为更复杂的组件,例如曲线和纹理。弧线可以是耳朵的边缘,方向盘的顶部或咖啡杯的边缘。这些中级模式被进一步组合以表示高级对象特征,例如头部,汽车或房屋。
由于 HTM 树状结构的设计,不同感知器感知到的资料也可以同时组合起来训练:
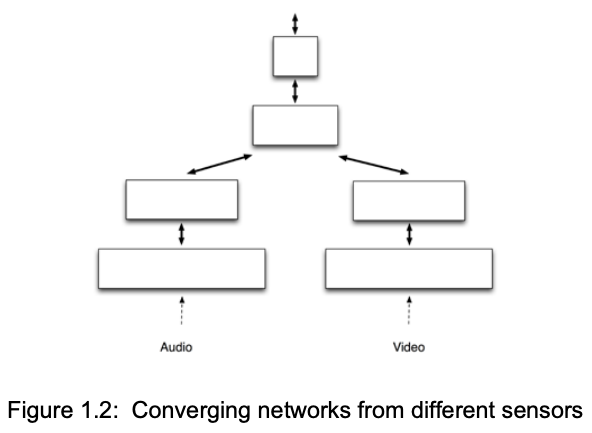
由于每个节点都会学到一个物体的模型(虽然不同阶层的节点会学到的东西的复杂度不一样),底层所学到的物体模型会逐层往上传递,所以 HTM 的泛化问题(Generalization)理论上应会比类神经网路容易处理。
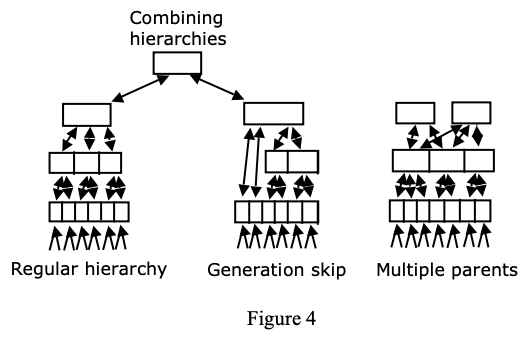
也因为这种树状结构,不同树间的结合、跳层传递以及注意力机制(Attention Mechanism)等等的想法可以轻易地在 HTM 中实现。
合并层次结构,跳过,多父级:
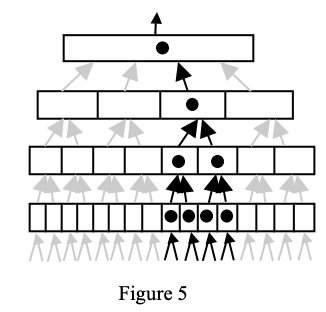
注意机制:
HTM 的 Region 可以理解为一个单一层,虽然我个人认为应该不需要特意限制一层只能有一个 Region。Region 的切面图如下图:
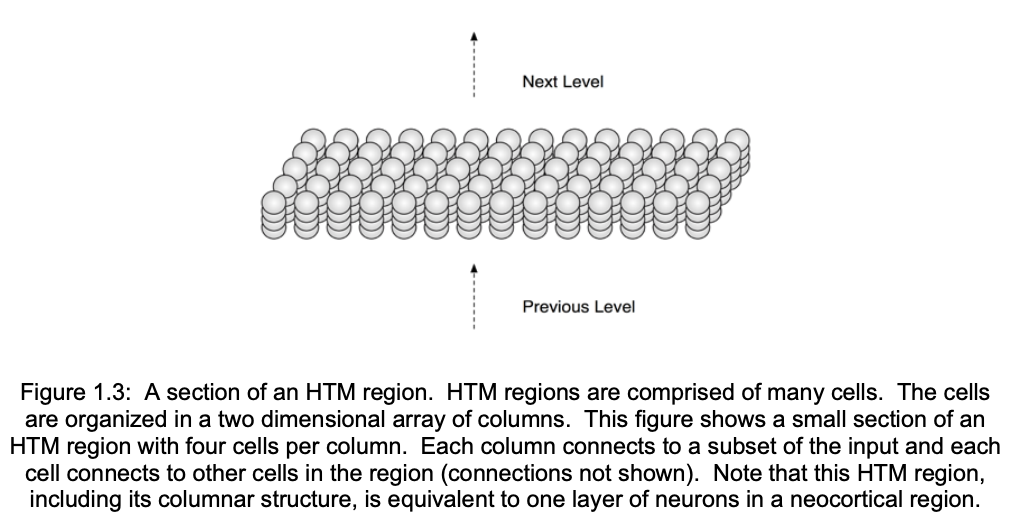
同一层之间的 Column 之间也有突触互相连结,这点跟类神经网路有点不同,通常类神经网路的节点只跟前后层节点有连结。
神经元
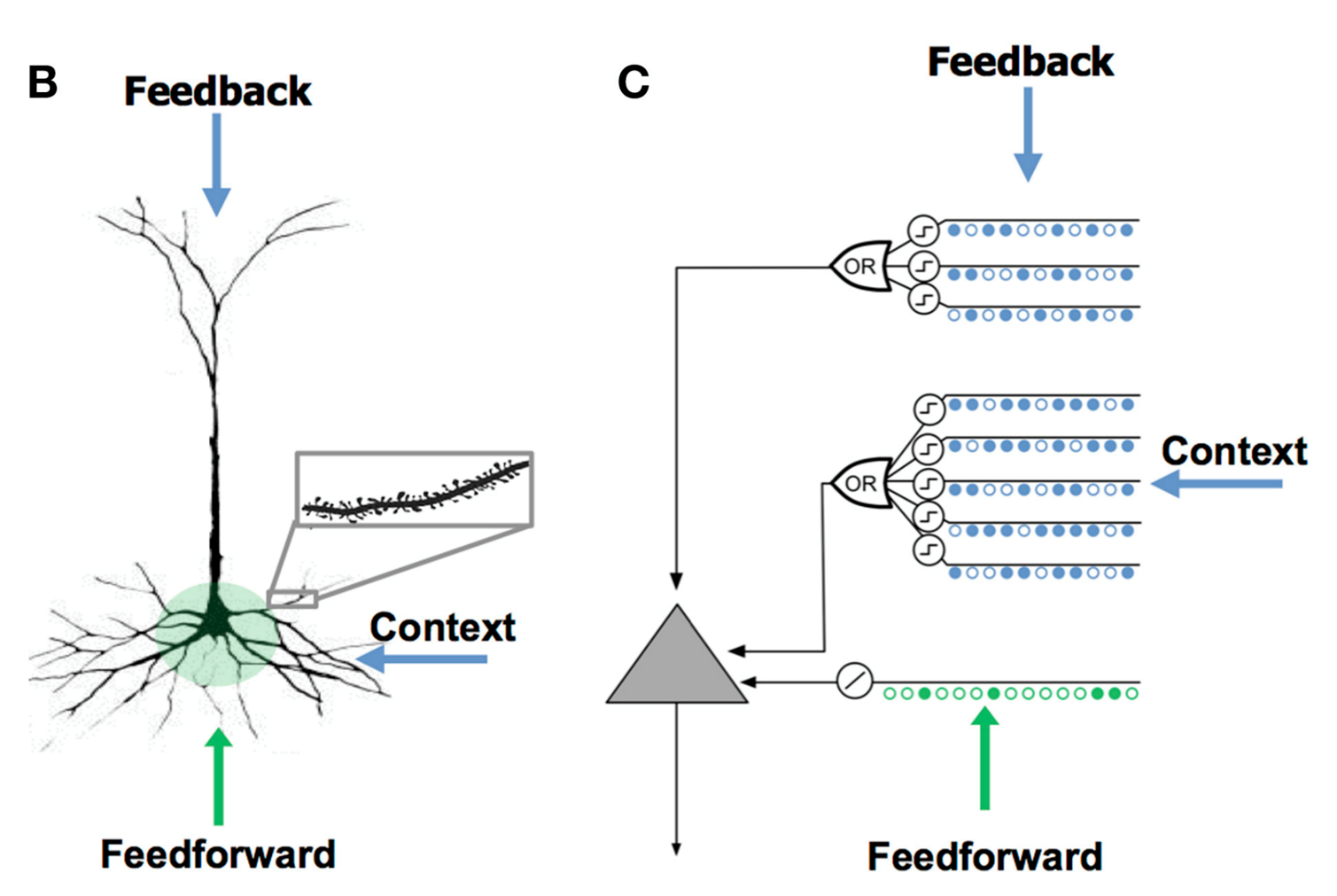 上图中B表示的是锥体细胞(pyramidal cell),是新皮质主要的神经细胞,其有三种树突(dendrite): 近端树突(proximal dendrites), 近端树突接受前馈输入信息;末端/基底树突(distal/basal dendrites),基底树突接受情境信息(context), 数量比近端树突多很多;顶端树突(apical dendrites),接受反馈信息,其一般接收上一层或几层的信息。图C则表示HTM中使用的、用以模拟锥体细胞的人工神经元,后文中统一称为单元(cell)。顶端树突接受反馈信息,在现阶段的模型当中,为简化,不予考虑。
上图中B表示的是锥体细胞(pyramidal cell),是新皮质主要的神经细胞,其有三种树突(dendrite): 近端树突(proximal dendrites), 近端树突接受前馈输入信息;末端/基底树突(distal/basal dendrites),基底树突接受情境信息(context), 数量比近端树突多很多;顶端树突(apical dendrites),接受反馈信息,其一般接收上一层或几层的信息。图C则表示HTM中使用的、用以模拟锥体细胞的人工神经元,后文中统一称为单元(cell)。顶端树突接受反馈信息,在现阶段的模型当中,为简化,不予考虑。

HTM在实际应用过程中,一般会按照上图所示框架进行建模:原始数据进入数据编码器中,编码成二进制向量;然后再经HTM的空间池化(Spatial Pooling,SP)算法生成稀疏分布式代表元(Sparse Distributed Representation, SDR);既而经HTM时间记忆(Temporal Memeory,TM)生成预测向量(也是SDR类型),最后将SDR输到分类器中进行分类预测,或其他函数、算法、模型中,实现所需目的。接下来,进行分块详述:数据编码(data encoding)、空间池化(spatial pooling)和时间记忆(temporal memery)。
数据编码(data encoding)
HTM模拟新大脑皮质,而大脑皮质接收的数据对其功能有重要影响。神经科学已有很多研究表明感觉器官将接收到的信息转化成稀疏数据。如耳蜗上面的绒毛细胞:
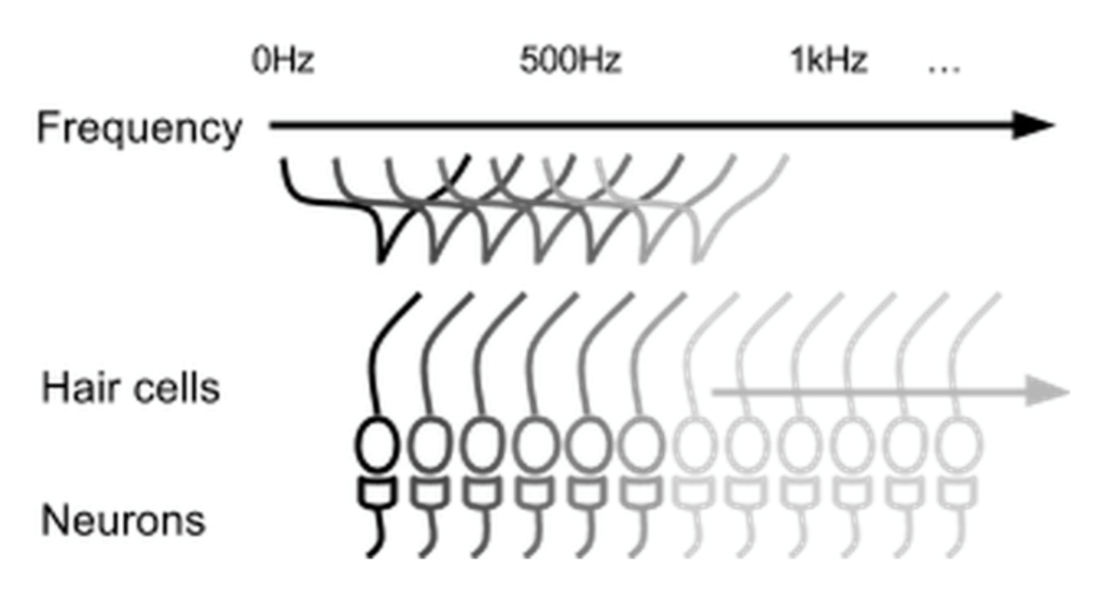
上图中,人可能听到的声音的频率从20Hz到比如20kHz,每个绒毛细胞如图能够接受一定范围的声音频率,即当声音频率在某个绒毛细胞可接受的频率范围,则绒毛细胞(或者可以说绒毛细胞下面的神经元,注:这里的神经元不同于新皮质内的神经元细胞)被激活。当声音(比如500Hz)传到耳蜗时,可接受此频率的绒毛细胞全部被激活。但其数量占绒毛总量的比例也是非常小的。从中可发现一些性质:数据输入是冗余的,即多个绒毛细胞可接受声音范围有重叠(Overlap),当同一信息输入时,多个绒毛细胞会被激活;信息在整个绒毛细胞列是稀疏的(Sparse)。
数据通过编码器将原始数据转化成新皮质可用数据,需满足:
- 语义相似数据应生成有重叠的激活位点(bits);
- 相同输入总产生固定长度的二进制向量;
- 输出的二进制向量应有相同维度(位点总数);
- 二进制向量应有相似的稀疏度,并且有足够的位点忍受噪音,以及子采样(subsampling)
数据输入
Sparse distributed representations (SDR)稀疏分布式代表元,超大容量(tremendous capacity),极度容忍噪声(extremely tolerant). SDR对学习和记忆系统特别方便(之前的版本中,原始数据经编码过程产生的Output被命名为SDR, 但最新版放弃了这种说法,转而把Spatial Pooling过程产生的output称为SDR;不过encoder产生的output也完全符合SDR性质,为叙述方便,不加区分,统称为SDR,至于代指哪一个过程,根据上下文过程可很容易区分)。输入到单元(cell)内的数据来自三种区域:
- 近端树突(proximal dendrites/zone): 授受前馈输入,即接受原始数据经encoder产生的SDR, 定义最优感受野(classic receptive field),通常,同一个细胞列(柱)内分享同一近端树突;
- 远端树突(distal dendrites/basal zone):接受背景环境输入, 即接受同一区域(region)的SDR,也就是与同一层内的其它单元产生连接突触(注region一词指代不清,也因目前的算法发展层面,接下来假设每一层都只有一个区域,这种简化只是方便叙述,对理解,及对模型几乎没有影响。), 学习序列转换,即学习数据的时间结构;
- 顶端树突(apical dendrites/apical zone): 接受反馈输入,唤起自上而下的‘序列’期望。
树突建模
数据编码成上述模式,还有一个很重要的原因,即在接下来的算法过程中,最主要用到的运算为Overlap及Union. 这两个算法都是二进制运算,最多可算是非常简单的矩阵运算,很大程度上减小运算的时空耗费。而接下来的运算区域或运算过程都是在树突上进行。
1、Overlap: 用以衡量两个SDR相似性:
$$overlap(\boldsymbol{x, y})=x \cdot y$$
其中x, y为两SDR向量,$\cdot$表示向量点乘,此过程可简单理解为对‘1’进行计数。如果overlap值超过一定阈值,比如$\theta$,就称两个SDR匹配(下面的x,y均为向量):
$$match(x, y) \equiv overlap(x, y) \ge \theta$$
2、Union: 赋予HTM在一个固定长度代表元上存储大量模式的能力。这个能力使得HTM可以实时预测(在TM阶段):
$$Union(x_1, x_2, \dots)=\oplus(x_1, x_2, \dots)$$
其中$\oplus$表示逐元素相加$x_i$表示SDR向量。
空间池化(spatial pooling)
Spatial Pooling是一种将输入讯号转变为Sparse Distributed Representation pattern的方法。“Pooling”这个字在论文中用来代指由输入讯号空间(较大空间)映射到Cortical region的sparse distributed representation空间(较小空间)所产生的、数学上的多对一映射问题。
基本原理是,对于每一个输入信号的bit(0或1),指定一个Column与其连接,并计算突触的最终输出值。如果突触的输出值大于一个阀值,就称这个突触进入激发态。接着对每一个Column,计算有多少突触进入激发态,并将这个值乘上一个“boosting factor”。即可得知这个Column是否进入激发态。由于每个Column的激发与否都会与其相邻的Column激发与否有关(计算在Boosting factor中),Spatial Pooling引入了一个「抑制半径」(inhibition radius)的观念,每个Column对于其他Column的影响一旦超过抑制半径即不予考虑(一样设计在Boosting factor中)。经过这几个步骤之后,我们即可得到如sparse distributed representation。Spatial Pooling的结果,是得到输入资料在空间上的pattern。而所谓的「训练」即是让HTM在以标记的资料中记住pattern。类似的pattern会被记住,因为那代表不同的输入讯号(来自同一个物体)所拥有的主要结构;反之,不常见的pattern则会被忘掉,如以下流程:
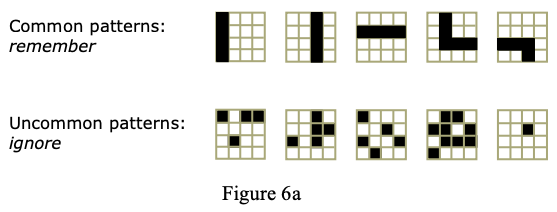
整个Spatial Pooling的演算法,演算法分三步:
- 在每个Column上找出输入造成的synapses overlap
- 找出被激发的candidate column,计算抑制半径
- update column的内部值
阶段1:重叠(Overlap)
for c in columns:
overlap(c) = 0
for s in connectedSynapses(c):
overlap(c) = overlap(c) + input(t, s.sourceInput)
if overlap(c) < minOverlap:
overlap(c) = 0
else:
overlap(c) = overlap(c) * boost(c)
阶段2:抑制
for c in columns:
minLocalActivity = kthScore(neighbors(c), desiredLocalActivity)
if overlap(c) > 0 and overlap(c) >= minLocalActivity:
activeColumns(t).append(c)
阶段3:学习
for c in activeColumns(t):
for s in potentialSynapses(c):
if active(s):
s.permanence += permanenceInc
s.permanence = min(1.0, s.permanence)
else:
s.permanence -= permanenceDec
s.permanence = max(0.0, s.permanence)
for c in columns:
minDutyCycle(c) = 0.01 * maxDutyCycle(neighbors(c))
activeDutyCycle(c) = updateActiveDutyCycle(c)
boost(c) = boostFunction(activeDutyCycle(c), minDutyCycle(c))
overlapDutyCycle(c) = updateOverlapDutyCycle(c)
if overlapDutyCycle(c) < minDutyCycle(c):
increasePermanences(c, 0.1 * connectedPerm)
inhibitionRadius = averageReceptiveFieldSize()
SpatialPooler(SP): SP对前馈连接进行建模,负责将二进制输入数据转化成SDR。SP即是对数据的空间(spatial)信息进行提取。SP须满足的属性:
- fixed sparseness固定稀疏性,即编码器出来的数据
- Distributed coding分布式编码
- Preserving semantic similarity保留语义相似性
- Noise robustness/fault tolerance噪声、错误的容忍
- Continuous learning连续学习
- Stability稳定性
前几个属性,因产生的是SDR即可满足,而后面的诸如连续学习,稳定性则是通过学习(突触连接控制得到的)。
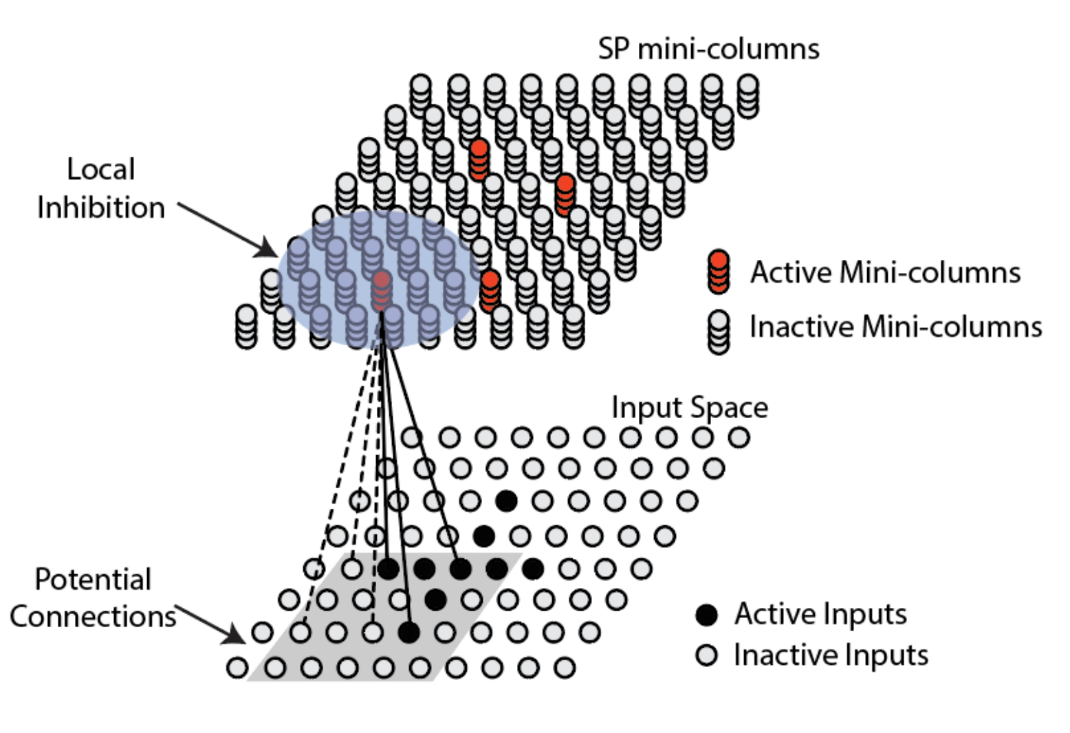
标准感受野
SP模型的第一步是确定标准感受野(Classic Receptive Field)(上图中的灰色方框),即每个单元柱(mini-column)读取输入数据的区域,也就是说每个单元柱只读取输入数据的一部分,而且相邻单元柱的标准感受野是有重叠的(overlap)。标准感受野确定之后,则要确定其中的潜在突触连接(potential connection)。所谓潜在连接即为单元柱可以形成与数据形成连接突触:
$$PotentialInput(i) = \{j|I(x_j,x_i^c,\gamma)\ and\ Z_{ij}
局部抑制
SP还对局部抑制(local inhibition)机制进行建模,也称'赢家通吃'原则,即,在第i个单元柱及其n个相邻单元柱中,如果第i个单元柱排在前k(k
持久度:前馈连接遵从赫布规则(hebbian rule): 对于每一个激活的单元柱的所有潜在连接,加强激活的突触连接,即增大其持久度(+p); 惩罚未激活的突触连接,即减小其持久度(-p),但不能超过1,或小于0。如果超过1就按1处理,小于0当0处理,即遵从截尾效应。
提升值:通过比较每一个单元柱与其相邻单元柱的近期活性(recent activity),第i个单元柱在t时刻的活性表示为$a_i(t)$, 定义第i个单元柱的近期活性表示为:
$$\bar{a}_i(t)=\frac{(T-1)*\bar{a}_i(t-1) +a_i(t)}{T}$$
参数T控制提升值的更新速度(趋势惯性)。
相邻单元柱的近期活性定义为:
$$<\bar{a}_i(t)>=\frac{1}{|Neighbor(i)|}\sum_{j\in Neighbor(i)}\bar{a}_j(t)$$
更新提升值$b_i$:
$$b_i=exp(-\beta(\bar{a}_i(t)-<\bar{a}_i(t)>))$$
局部抑制半径$\phi$:
所有单元柱突触连接的平均值与每个输入神经元的连接单元柱数量乘积。
SP总结
- 经SP过程,产生真正意义上的SDR。SP过程,有多个步骤使数据稀疏化(当然这些步骤是在完成提取必要信息的过程中完成的稀疏化):第一个是潜在连接的产生过程(当然目前,算法的p值设为1,没有实际意义,但不应该忽略其作用);第二个是根据持久度形成的突触连接;第三个是竞争性局部抑制。
- SP后,产生的SDR维度与这一层的维度一致(即在目前算法中,为一个M维向量,这里的M为本层内单元柱的个数)。
SP激活的最小单位是单元柱,这也是前面强调的,同一单元柱内的单元共享近端树突的数据输入。其中提取的是数据的空间特征。
时间记忆(Temporal Memory)
Temporal Memory的基本概念是学习Spatial pattern的时间序列,如下图所示:
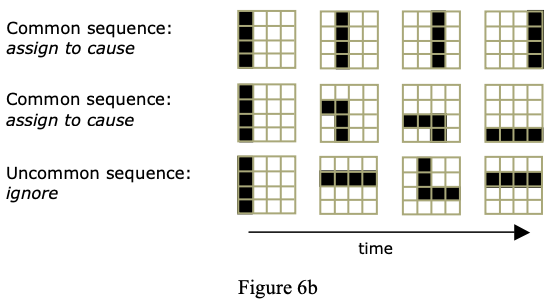
TM算法是HTM最核心的算法,正因为TM, HTM才具备的学习及预测能力。当SDR输入到TM中,学习SDR中所代表的数据及其背景环境(context)。学习:通过增加或者减少潜在突触连接而达到学习目的。预测:根据SDR预测。基于过去与当前对未来进行预测。
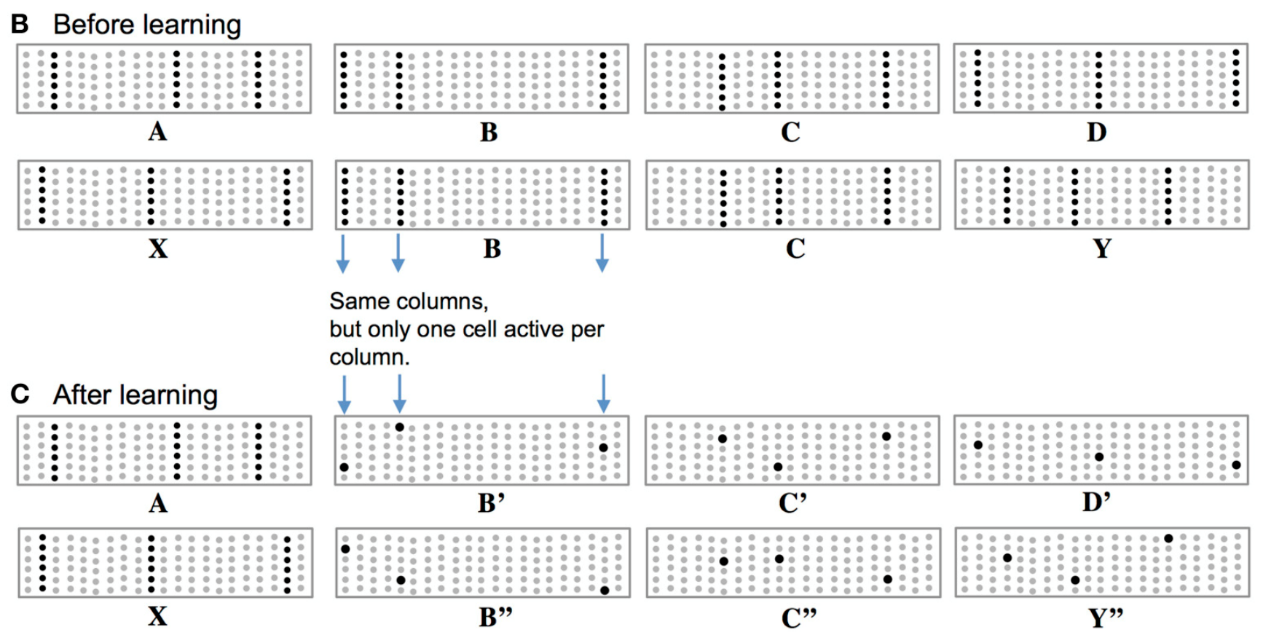
上图中可视为TM的一个学习过程。在SP阶段,数据输出SDR,其中提取的只能显示出空间特性,而时间特征,则需要在TM阶段过程提取,而提取过程中数据的学习,则是通过学习数据模式(pattern)的方式,而模式的表示则需要‘精确’到单元柱中的单元。上图B中,序列BC分别在序列ABCD与XABY中出现,经SP过程两序列中BC的表却是相同的(见上图B中B,C表示)。为既能体现BC是相同的,又要体现两序列中BC处在不同的情境(context)中,HTM采用的做法是在同一单元柱内用不同的单元表示(如上图C中B'C'与B''C'')。
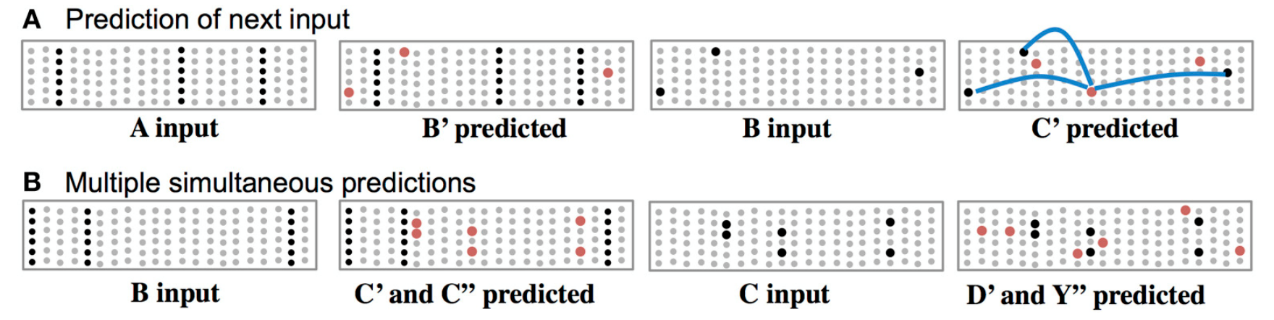
学习过程紧跟着预测过程。上图A中A输入后,TM预测出B(图中红点)出如果B成功预测,则接下来会预测C。上图B中,当输入B时,会预测C, 但由于此时C不唯一,TM会两种情况都给出(C',C''),输入‘C'同理会给出D',Y'两种预测。
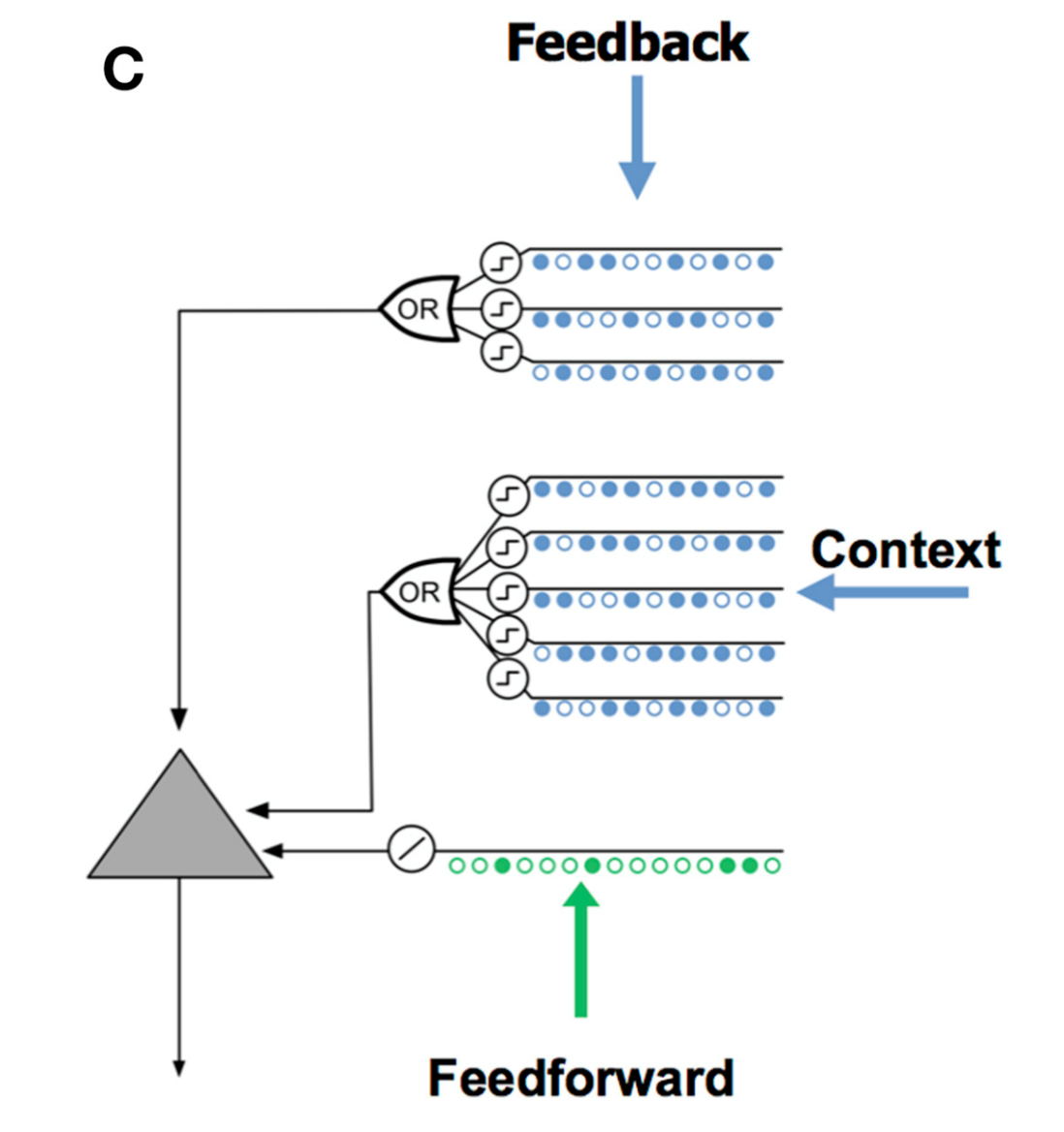
在TM阶段,用到的树突是基底树突,即上图标有Context处。基底树突相较于前馈输入的近端树突,其数会很大,一个单元中蕴含多个基底树突。基底树突是HTM的记忆系统,这里储存着大量的HTM学习到的数据模工,这些模式是预测的基础。每个树突都含有一个MXN的模式矩阵,且是稀疏的,大量的模式包含在这个矩阵中(以Union('OR')的形式储存)。
基本参数:
- N:单元柱数量
- M:每个单元柱所含单元数
- D:每个单元所含基底树突数
- S:每个基底突触所突触数
- $A^t$:t时刻激活状态矩阵,其中$a_{ij}^t$表示在t时刻,第j个单元柱上第i个单元的状态
- $\Pi^t$:t时刻单元预测状态矩阵,其中$\pi_{ij}^t$表示在t时刻,第j个单元柱上第i个单元的预测状态;
- $D_{ij}$:单元基底树突集,其中$D_{ij}^d$表示$a_{ij}^t$第j个单元柱上第i个单元的第d个基底树突,为一稀疏矩阵(MXN),其中非0元素代表,潜在突触的持久度
- $\dot{D}_{ij}^d$:MXN的0,1矩阵,其中元素1所处位置表示处此处的$D_{ij}$的持久度为非0(>0)
- $\tilde{D}_{ij}^d$:MXN的0,1矩阵,其中元素1所处位置表示此处形成突触连接
上图是TM的动态演示,动得太快有点乱,这里就不作过多关注,只需对其中连接有个直观认识即可。
初始化:
随机选取一组单元,并为这些单元的基底树突分配随机分配持久度,同SP阶段一样,持久度是调节突触连接的关键,是需要学习的参数,也正因为持久度的变化,才能使得HTM具备了学习的能力。这里的树突不是层与层间的树突,而是同一层内,一个单元与其他所有单元的连接突触。
计算单元状态:
局部抑制过程作用之后(SP过程之后),一组激活的单元柱($W^t$)产生,现在来计算单元柱中每个单元的状态,则:
$$a_{ij}^t =\left\{\begin{array}\\1,\quad j\in W^t,\pi_{ij}^{t-1}=1;\\1,\quad j\in W^t,\sum_{i}\pi_{ij}^{t-1}=0;\\0,\quad otherwise.\end{array}\right.$$
上式表示,当单元处于激活单元柱中,并且处在预测状态(predictive state)(即在t-1时刻被预测为t时刻要被激活),则此单元即被激活;或者单元处在激活单元柱中,但所在单元柱中所有单元均不处于预测状态,则被激活(这句话说明,如果所处激活单元柱中所单元都不处于激活状态,则单元柱上的所有单元均被激活)。
而单元的预测状态:
$$\pi_{ij}^t=\left\{\begin{array}\\1,\quad \exists_d\left\|\tilde{D}_{ij}^d\circ A^t\right\|_1>\theta;\\0,\quad otherwise.\end{array}\right.$$
其中$\theta$表示预测状态激活阈值,$\circ$表示逐元素相乘。即当某一单元的任意基底树突与状态矩阵的突触连接数大于预测状态阈值,单元则处于激活状态。
更新树突及突触:1、更新树突选择
TM的学习及预测的物理基础即为树突的长衰,而树突的长衰则是通过树突的持久度来调节。那第一步即是选择要更新的树突。设要更新的树突集合为$D_u$,则:
$$D_{u1}:\left\{D_{ij}^d\\Big|\\ \forall_{j\in W^t}\left(\pi_{ij}^{t-1}>0\right)and \left\|\tilde{D}_{ij}^d\circ A^{t-1}\right\|>\theta\right\}$$
$D_{u1}$表示那些成功预测的单元基底树突。
如果激活的单元柱为非预测的,需要选择其中一个单元(选择基底树突包含持久度最大的那个单元)表示数据及其情境,为未来预测作准备:
$$D_{u2} :\left\{D_{ij}^d\\Big|\\ \forall_{j\in W^t}\left(\sum_{i}\pi_{ij}^{t-1}=0\right)and\left\|\dot{D}_{ij}^d\circ A^{t-1}\right\|=\max_{i}\left(\left\|\dot{D}_{ij}^d\circ A^{t-1}\right\|_1\right)\right\}$$
则需要更新的树突集合为:
$$D_u=D_{u1}+D_{u2}$$
2、持久度更新
更新的原则遵从赫布规则:奖励激活单元的突触,惩罚非激活单元突触,具体实施,即增加、减小持久度:
$$D_{ij}^d:=D_{ij}^d+\Delta D_{ij}^d$$
其中$\Delta D_{ij}^d$即为拷久度变化值,其可分为两种情况:一是对于激活单元;另一种是对那些并未激活的单元(即预测失败的单元),给予其微小的衰减,因为
$$\Delta D_{ij}^d=\left\{\begin{array}\\p^+\left(\dot{D}_{ij}^d\circ A^{t-1}\right)-p^-\dot{D}_{ij}^d,&&\quad a_{ij}^t=1;\\p^{--}\dot{D}_{ij}^d,&&\quad a_{ij}^t=0\and\\left\|\tilde{D}_{ij}^d\circ A^{t-1}\right\|>\theta.\end{array}\right.$$
处理步骤:
Inference Only—Phase1:
for c in activeColumns(t):
buPredicted = false
for i = 0 to cellsPerColumn - 1:
if predictiveState(c, i, t - 1) == true:
s = getActiveSegment(c, i, t - 1, activeState)
if s.sequenceSegment == true:
buPredicted = true
activeState(c, i, t) = 1
if buPredicted == false:
for i = 0 to cellsPerColumn - 1:
activeState(c, i, t) = 1
Inference Only—Phase2
for c, i in cells:
for s in segments(c, i):
if segmentActive(c, i, s, t):
predictiveState(c, i, t) = 1
Inference + Learning—Phase1
for c in activeColumns(t):
buPredicted = false
lcChosen = false
for i = 0 to cellsPerColumn - 1:
if predictiveState(c, i, t - 1) == true:
s = getActiveSegment(c, i, t - 1, activeState)
if s.sequenceSegment == true:
buPredicted = true
activeState(c, i, t) = 1
if segmentActive(s, t - 1, learnState):
lcChosen = true
learnState(c, i, t) = 1
if buPredicted == false:
for i = 0 to cellsPerColumn - 1:
activeState(c, i, t) = 1
if lcChosen == false:
I, s = getBestMatchingCell(c, t - 1)
learnState(c, i, t) = 1
sUpdate = getSegmentActiveSynapses(c, i, s, t - 1, true)
sUpdate.sequenceSegment = true
segmentUpdateList.add(sUpdate)
Inference + Learning—Phase2
for c, i in cells:
for s in segments(c, i):
if segmentActive(s, t, activeState):
predictiveState(c, i, t) = 1
activeUpdate = getSegmentActiveSynapses(c, i, s, t,
false)
segmentUpdateList.add(activeUpdate)
predSegment = getBestMatchingSegment(c, i, t - 1)
predUpdate = getSegmentActiveSynapses(c, i, predSegment,
t - 1, true)
segmentUpdateList.add(predUpdate)
Inference + Learning—Phase3
for c, i in cells:
if learnState(s, i, t) == 1:
adaptSegments(segmentUpdateList(c, i), true)
segmentUpdateList(c, i).delete()
elseif predictiveState(c, i, t) == 0
and predictiveState(c, i, t - 1) == 1:
adaptSegments(segmentUpdateList(c, i), false)
segmentUpdateList(c, i).delete()
使用HTM进行时间序列异常检测
相关项目:
- HTM算法:https://github.com/numenta/nupic
- NAB(性能对比):https://github.com/numenta/NAB
- https://github.com/yyccR/AnomalyDetection
- https://github.com/flarelink/HTM_Streaming_Anomaly
参考链接: