在Apriori算法的学习中,我们了解到Apriori算法需要不断生成候选项目队列和不断得扫描整个数据库进行比对,I/O是很大的瓶颈。为了解决这个问题,FP-Growth利用了巧妙的数据结构,无论多少数据,只需要扫描两次数据集,大大降低了Aproir挖掘算法的代价。FP-Growth算法主要包含有两个步骤:
- 建立一个精简的数据结构:FP-tree(frequent-pattern tree,频繁模式树)
- 从FP-tree中提取频繁项集
FP-Growth算法原理
为了减少I/O次数,FP-Growth算法引入了一些数据结构来临时存储数据。这个数据结构包括三部分,如下图所示:
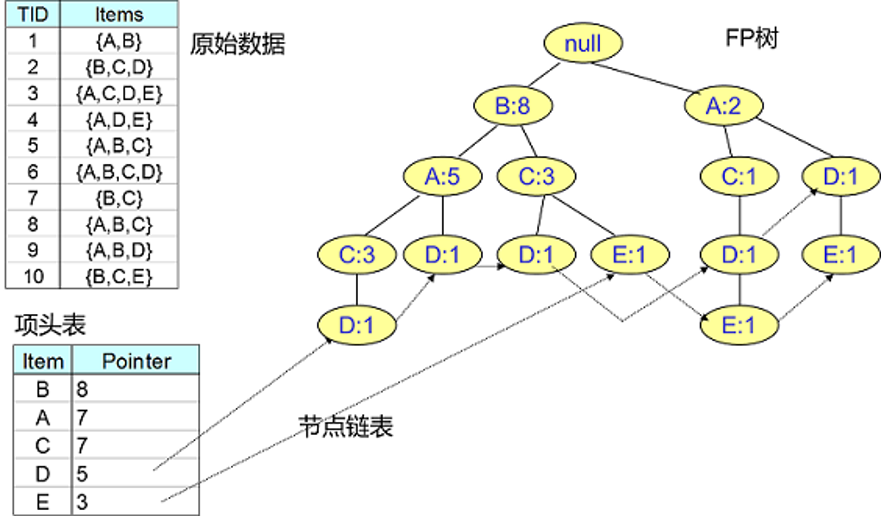
- 第一部分是一个项头表。里面记录了所有的1项频繁集出现的次数,按照次数降序排列。比如上图中B在所有10组数据中出现了8次,因此排在第一位,这部分好理解。
- 第二部分是FP-Tree,它将我们的原始数据集映射到了内存中的一颗FP树
- 第三部分是节点链表。所有项头表里的1项频繁集都是一个节点链表的头,它依次指向FP树中该1项频繁集出现的位置。这样做主要是方便项头表和FP-Tree之间的联系查找和更新,也好理解。
我们以下面的数据为例进行详细了解:
上面的流程讲的有些迷糊,我们用一个数据举例:定义”TID”为订单ID,”Items bought”为一次订单内购买的商品:
| TID | Items bought |
| 100 | {f,a,c,d,g,i,m,p} |
| 200 | {a,b,c,f,l,m,o} |
| 300 | {b,f,h,j,o} |
| 400 | {b,c,k,s,p} |
| 500 | {a,f,c,e,l,p,m,n} |
建立项头表
在构建FP-Tree之前,首先要建立一张项头表。扫描原始数据,并对每个商品进行计数。在这里可以设置阈值,比如保留最少要出现三次的商品。筛选后剩下a,b,c,f,m,p这六个商品,将这些商品按数量降序排列,生成项头表。
| Item | Count |
| f | 4 |
| c | 4 |
| a | 3 |
| b | 3 |
| m | 3 |
| p | 3 |
筛选排序原始数据
接下来开始第二次扫描原属数据,对于每条数据,剔除非项头表上的商品,并按照支持度降序排列。比如订单100,购买商品为{f,a,c,d,g,i,m,p},剔除数据后为{f,a,c,m,p},排序后为{f,c,a,m,p}。其他的原始数据以此类推进行处理,得到排序后的数据集。
| TID | Items bought | (Ordered) frequent items |
| 100 | {f,a,c,d,g,i,m,p} | {f,c,a,m,p} |
| 200 | {a,b,c,f,l,m,o} | {f,c,a,b,m} |
| 300 | {b,f,h,j,o} | {f,b} |
| 400 | {b,c,k,s,p} | {c,b,p} |
| 500 | {a,f,c,e,l,p,m,n} | {f,c,a,m,p} |
构建FP-Tree
有了项头表和筛选排序后的原始数据集,接下来就可以构建FP-Tree了。建立FP-Tree需要我们一条条的读取筛选排序后的原始数据,并按照顺序依次插入到树中。如果有公共的祖先节点,则在对应的祖先节点加1。同时,新节点出现时,需要将其链接到项表头对应的节点链表。直到所有数据都插入树中,则构建完成。
接下来还是用上面的数据举个例子。首先插入TID100,此时FP-Tree没有其他节点,因此{f,c,a,m,p}是一个独立的路径,所有节点计数为1,项头表通过节点链表链接上对应的新增节点。
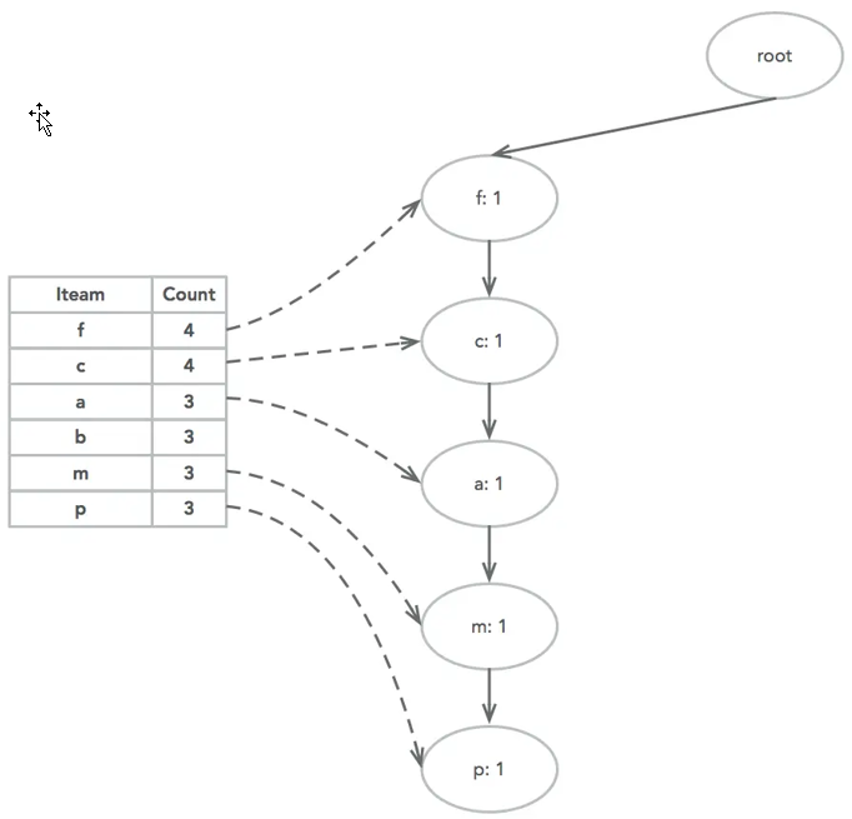
接着插入TID200,{f,c,a,b,m},其中f、c、a三个节点公用,计数变为2,到b节点产生新的分支,m为b的子节点,两个节点计数为1。当然,对应的b、m两个节点的链表也要更新。
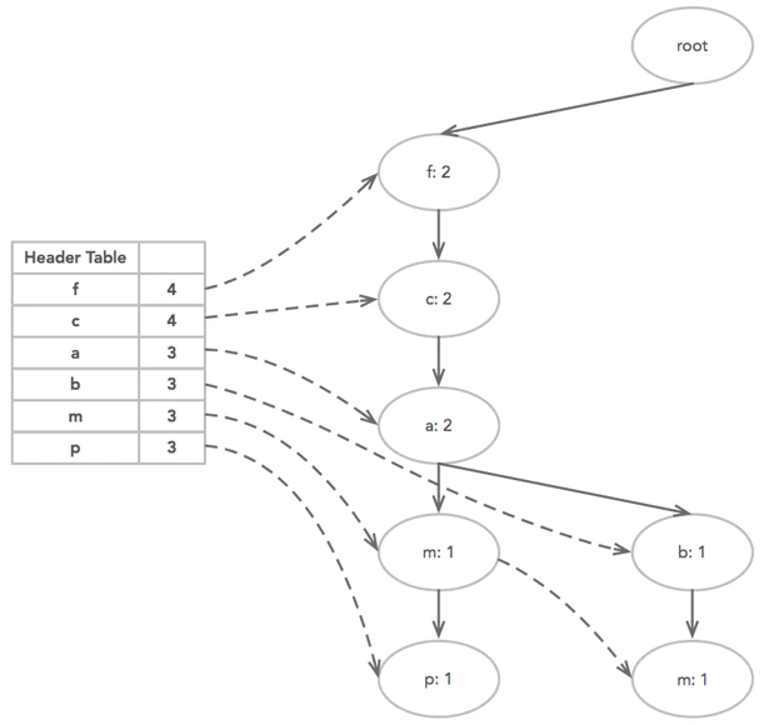
依次处理剩下的三条数据,构建完成FP-Tree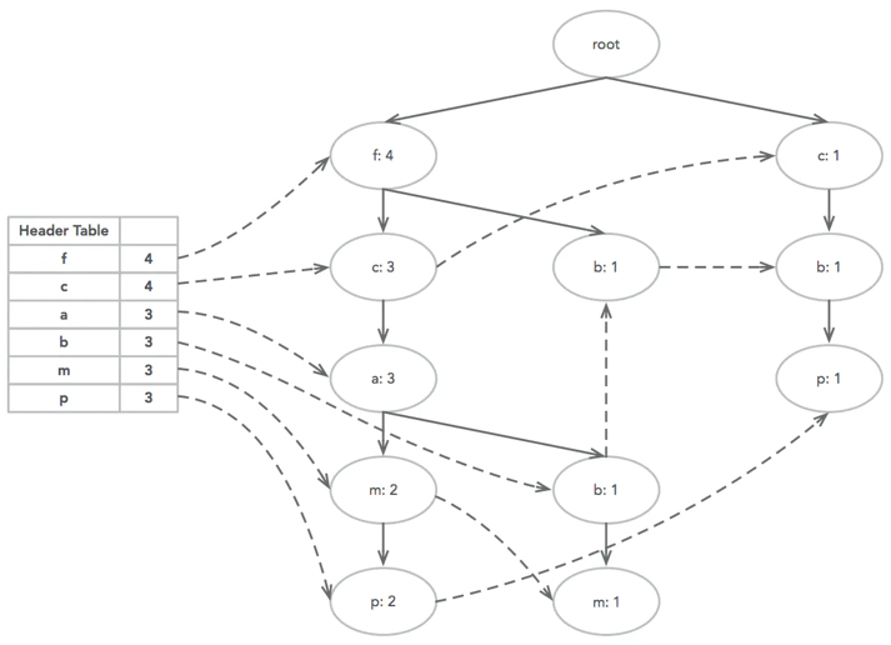
挖掘频繁项集
准备好了FP-Tree,接下来就可以开始挖掘频繁项集。遍历项头表依次挖掘,找到每项的条件模式基。条件模式基是以要挖掘的节点作为叶子节点所对应的子树。得到这个子树,将子树中每个节点的的计数设置为叶子节点的计数,并删除计数低于约定值的节点。从这个条件模式基,我们就可以递归挖掘得到频繁项集了。假设需要的最小节点计数为2,开始挖掘p节点,如下图所示:
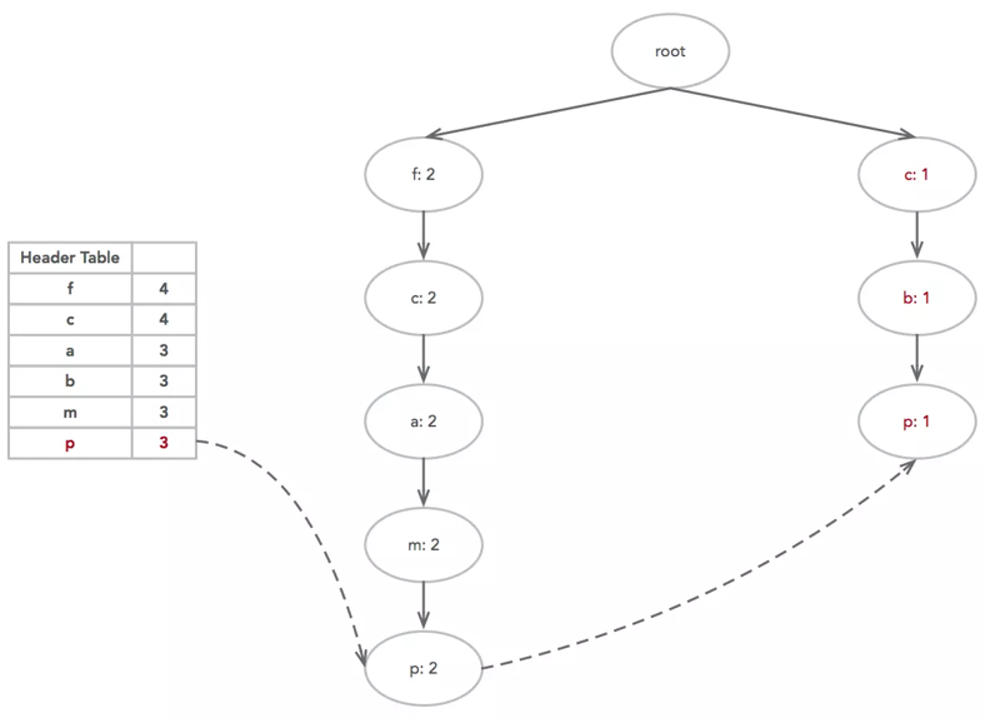
删除图中节点计数小于2的红色{c:1}、{b:1}、{p:1}节点,得到{p:2}节点的条件模式基为{f:2,c:2,a:2,m:2}。通过它,可以递归得到频繁二项集{f:2,p:2}、{c:2,p:2}、{a:2,p:2}、{m:2,p:2},频繁三项集{f:2,c:2,p:2}、{f:2,a:2,p:2}等等,最后得到最大的频繁项集为频繁五项集,为{f:2,c:2,a:2,m:2,p:2}。如果最小节点计数为1,则可在挖掘完上面的子树后,根据项表头对应的节点链表找到红色的节点{p:1},继续挖掘频繁项集。至此,p节点挖掘完毕,可以继续挖掘其他节点。挖掘完所有节点,也就得到了所有的频繁项集。至于最后f节点,由于它的条件模式基为空,因此可以不用去挖掘。
FP-Growth的Python实现
```python
class treeNode: # node class include properties and methods of node
def __init__(self, name_value, num_occur, parent_node):
self.name = name_value # value is node string
self.count = num_occur # value is int
self.node_link = None # value is class_node
self.parent = parent_node # value is class_node
self.children = {} # content is node.name: class_node
def inc(self, num_occur):
self.count += num_occur # count node
def displaces(self, ind=1):
print(' ' * ind, self.name, ' ', self.count)
for child in self.children.values():
child.displaces(ind + 1) # iteration output
# update items header forms
def update_header(node_test, target_node):
while node_test.node_link is not None:
node_test = node_test.node_link
node_test.node_link = target_node
# update iteratly tree (top to down)
def update_tree(items, in_tree, header_table, count):
if items[0] in in_tree.children:
in_tree.children[items[0]].inc(count)
else:
in_tree.children[items[0]] = treeNode(items[0], count, in_tree) # build branch
if header_table[items[0]][1] is None:
header_table[items[0]][1] = in_tree.children[items[0]]
else:
update_header(header_table[items[0]][1], in_tree.children[items[0]])
if len(items) > 1:
update_tree(items[1:], in_tree.children[items[0]], header_table, count)
# build FP-Tree
def creat_tree(data_set, min_sup=1): # data_set is dictionary
header_table = {}
for trans in data_set:
for item in trans:
header_table[item] = header_table.get(item, 0) + data_set[trans]
for item_1 in list(header_table.keys()):
if header_table[item_1] < min_sup:
del(header_table[item_1])
fre_item_set = set(header_table.keys())
if len(fre_item_set) == 0:
return None, None
for item_1 in header_table:
# items header table includes name and node count and address of node
header_table[item_1] = [header_table[item_1], None]
ret_tree = treeNode("Null Set", 1, None) # root node
for trans_set, count in data_set.items():
local_id = {}
for item_1 in trans_set:
if item_1 in fre_item_set:
local_id[item_1] = header_table[item_1][0]
if len(local_id) > 0:
order_set = [v[0] for v in sorted(local_id.items(), key=lambda p: p[1], reverse=True)]
update_tree(order_set, ret_tree, header_table, count)
return ret_tree, header_table
def local_data():
test_data = [['r', 'z', 'h', 'j', 'p'],
['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
['z'],
['r', 'x', 'n', 'o', 's'],
['y', 'r', 'x', 'z', 'q', 't', 'p'],
['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
return test_data
# example dataset
def load_data():
test_data = [['I1', 'I2', 'I5'],
['I2', 'I4'],
['I2', 'I3'],
['I1', 'I2', 'I4'],
['I1', 'I3'],
['I2', 'I3'],
['I1', 'I3'],
['I1', 'I2', 'I3', 'I5'],
['I1', 'I2', 'I3']]
return test_data
def creat_set(data_set):
ret_dic = {}
for trans in data_set:
ret_dic[frozenset(trans)] = ret_dic.get(frozenset(trans), 0) + 1
return ret_dic
# search prefix tree
def before_tree(header_table_node, bef_path):
if header_table_node.parent is not None:
bef_path.append(header_table_node.name)
before_tree(header_table_node.parent, bef_path)
# search all prefix tree of the same node
def find_path(base_pat, tree_node):
cond_pats = {}
while tree_node is not None:
pre_path = []
before_tree(tree_node, pre_path)
if len(pre_path) > 1:
cond_pats[frozenset(pre_path[1:])] = tree_node.count
tree_node = tree_node.node_link
return cond_pats
# mine tree
def mine_tree(in_tree, header_table, min_sup, pre_path, fre_item_set, fre_item_count):
fre_item_1 = [v[0] for v in sorted(header_table.items(), key=lambda p: p[1][0])]
for base_pat in fre_item_1:
new_fre_set = pre_path.copy()
new_fre_set.add(base_pat)
# support count of frequent itemset
fre_item_count[frozenset(new_fre_set)] = header_table[base_pat][0]
fre_item_set.append(new_fre_set)
cond_pat_path = find_path(base_pat, header_table[base_pat][1])
my_tree, my_header = creat_tree(cond_pat_path, min_sup)
print("condition tree for:", new_fre_set)
if my_tree is not None:
my_tree.displaces(1)
if my_header is not None:
mine_tree(my_tree, my_header, min_sup, new_fre_set, fre_item_set, fre_item_count)
return fre_item_set, fre_item_count
# calculate support rate %
def support_grate(fre_item_count, trans_dic):
total_trans = sum(trans_dic.values())
for item_set in fre_item_count.keys():
```set_grate[item_set] = float(fre_item_count[item_set] / total_trans)
return set_grate
if __name__ == "__main__":
fre_item = []
fre_item_count = {}
set_grate = {}
sim_data = local_data()
set_data = creat_set(sim_data)
my_data_tree, my_header_table = creat_tree(set_data, 2)
my_data_tree.displaces() # print FP-Tree
fre_item, fre_item_count = mine_tree(my_data_tree, my_header_table, 2, set([]), fre_item, fre_item_count)
grate_sup = support_grate(fre_item_count, set_data)
print(fre_item)
print(fre_item_count)
print(grate_sup)
其他参考:



