CTR预估模型FM、FFM、DeepFM

点击率(click-through rate, CTR)是点击特定链接的用户与查看页面，电子邮件或广告的总用户数量之比。它通常用于衡量某个网站的在线广告活动是否成功，以及电子邮件活动的有效性，是互联网公司进行流量分配的核心依据之一。

$$CTR=\frac{number\,of\,click-throughs}{number\,of\,impressions}\times100\%$$

无论使用什么类型的模型，点击率这个命题可以被归纳到二元分类的问题，我们通过单个个体的特征，计算出对于某个内容，是否点击了，点击了就是1，没点击就是0。对于任何二元分类的问题，最后我们都可以归结到逻辑回归上面。

• 早期的人工特征工程+LR(Logistic Regression)：这个方式需要大量的人工处理，不仅需要对业务和行业有所了解，对于算法的经验要求也十分的高。
• GBDT(Gradient Boosting Decision Tree)+LR：提升树短时这方面的第二个里程碑，虽然也需要大量的人工处理，但是由于其的可解释性和提升树对于假例的权重提升，使得计算准确度有了很大的提高。
• FM-FFM：FM和FFM模型是最近几年提出的模型，并且在近年来表现突出，分别在由Criteo和Avazu举办的CTR预测竞赛中夺得冠军，使得到目前为止，还都是以此为主的主要模型占据主导位置。
• Embedding模型可以理解为FFM的一个变体。

CTR预估技术从传统的Logistic回归，到近两年大火的深度学习，新的算法层出不穷：DeepFM, NFM, DIN, AFM, DCN等。其实这些算法都是特征工程方面的模型，无论最后怎么计算，最后一层都是一个二元分类的函数（sigmod为主）。本文主要涉及三种FM系列算法：FM，FFM，DeepFM

FM（Factorization Machines，因子分解机）

FM（Factorization Machines，因子分解机）最早由Steffen Rendle于2010年在ICDM上提出，它是一种通用的预测方法，在即使数据非常稀疏的情况下，依然能估计出可靠的参数进行预测。与传统的简单线性模型不同的是，因子分解机考虑了特征间的交叉，对所有嵌套变量交互进行建模（类似于SVM中的核函数），因此在推荐系统和计算广告领域关注的点击率CTR（click-through rate）和转化率CVR（conversion rate）两项指标上有着良好的表现。此外，FM的模型还具有可以用线性时间来计算，以及能够与许多先进的协同过滤方法（如BiasMF、SVD++等）相融合等优点。

在介绍FM模型之前，来看看稀疏数据的训练问题。以广告CTR（click-through rate）点击率预测任务为例，假设有如下数据：

第一列Clicked是类别标记，标记用户是否点击了该广告，而其余列则是特征（这里的三个特征都是类别类型），一般的，我们会对数据进行One-hot编码将类别特征转化为数值特征，转化后数据如下：

经过One-hot编码后，特征空间是十分稀疏的。特别的，某类别特征有m种不同的取值，则one-hot编码后就会被变为m维，当类别特征越多、类别特征的取值越多，其特征空间就更加稀疏。

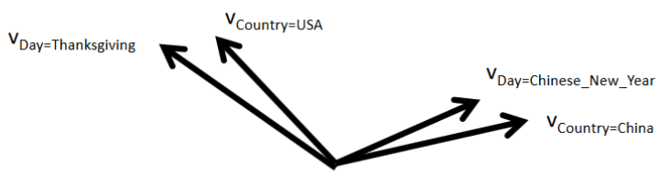
同时通过观察大量的样本数据可以发现，某些特征经过关联之后，与label之间的相关性就会提高。例如，”USA”与”Thanksgiving”、”China”与”Chinese New Year”这样的关联特征，对用户的点击有着正向的影响。换句话说，来自”China”的用户很可能会在”Chinese New Year”有大量的浏览、购买行为，而在”Thanksgiving”却不会有特别的消费行为。这种关联特征与label的正向相关性在实际问题中是普遍存在的，如”化妆品”类商品与”女”性，”球类运动配件”的商品与”男”性，”电影票”的商品与”电影”品类偏好等。因此，引入两个特征的组合是非常有意义的。

如何表示两个特征的组合呢？一种直接的方法就是采用多项式模型来表示两个特征的组合，$x_i$为第i个特征的取值，$x_ix_j$表示特征$x_i$和$x_j$的特征组合，其系数$w_ij$即为我们学习的参数，也是$x_ix_j$组合的重要程度：

$$\hat y(\mathbf{x})=w_0+\sum_{i=1}^dw_ix_i+\sum_{i=1}^d\sum_{j=i+1}^dw_{ij}x_ix_j$$

上式也可以称为Poly2(degree-2 poly-nomial mappings)模型。注意到式中参数的个数是非常多的，一次项有$d+1$个，二次项共有$\frac{d(d-1)}{2}$个，而参数与参数之间彼此独立，在稀疏场景下，二次项的训练是很困难的。因为要训练$w_{ij}$，需要有大量的$x_i$和$x_j$都非零的样本（只有非零组合才有意义）。而样本本身是稀疏的，满足$x_ix_j\ne0$的样本会非常少，样本少则难以估计参数$w_{ij}$，训练出来容易导致模型的过拟合。

为此，Rendle于2010年提出FM模型，它能很好的求解上式，其特点如下：

• FM模型可以在非常稀疏的情况下进行参数估计
• FM模型是线性时间复杂度的，可以直接使用原问题进行求解，而且不用像SVM一样依赖支持向量。
• FM模型是一个通用的模型，其训练数据的特征取值可以是任意实数。而其它最先进的分解模型对输入数据有严格的限制。FMs可以模拟MF、SVD++、PITF或FPMC模型。

FM模型原理

前面提到过，式中的参数难以训练时因为训练数据的稀疏性。对于不同的特征对$x_i,x_j$和$x_i,x_k$，认为是完全独立的，对参数$w_{ij}$和$w_{ik}$分别进行训练。而实际上并非如此，不同的特征之间进行组合并非完全独立，如下图所示：

回想矩阵分解，一个rating可以分解为user矩阵和item矩阵，如下图所示：

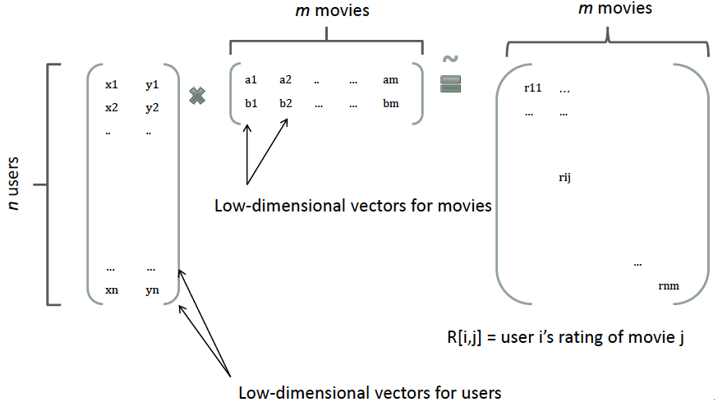
分解后得到user和item矩阵的维度分别为$nk$和$km$，（k一般由用户指定），相比原来的rating矩阵，空间占用得到降低，并且分解后的user矩阵暗含着user偏好，Item矩阵暗含着item的属性，而user矩阵乘上item矩阵就是rating矩阵中用户对item的评分。因此，参考矩阵分解的过程，FM模型也将上式的二次项参数$w_{ij}$进行分解：

$$\hat y(\mathbf{x})=w_0+\sum_{i=1}^dw_ix_i+\sum_{i=1}^d\sum_{j=i+1}^d(\mathbf{v}_i\cdot\mathbf{v}_j)x_ix_j$$

其中$v_i$是第i维特征的隐向量，其长度为$k(k\ll d)$。$(\mathbf{v}_i\cdot\mathbf{v}_j)$为内积，其乘积为原来的$w_{ij}$，即$\hat w_{ij}=(\mathbf{v}_i\cdot\mathbf{v}_j)=\sum_{f=1}^kv_{i,f}\cdot v_{j,f}$。

为了方便说明，考虑下面的数据集（实际中应该进行one-hot编码，但并不影响此处的说明）：

对于上面的训练集，没有（NBC，Adidas）组合，因此，Poly2模型就无法学习到参数$w_{NBC,Adidas}$。而FM模型可以通过特征组合(NBC，Nike)、(EPSN，Adidas)分别学习到隐向量$V_{NBC}$和$V_{Adidas}$，这样使得在测试集中得以进行预测。

更一般的，经过分解，式中的参数个数减少为$kd$个，对比上式参数个数大大减少。使用小的k，使得模型能够提高在稀疏情况下的泛化性能。此外，将$w_{ij}$进行分解，使得不同的特征对不再是完全独立的，而它们的关联性可以用隐式因子表示，这将使得有更多的数据可以用于模型参数的学习。比如$x_i,x_j$与$x_i,x_k$的参数分别为：$\langle\mathbf{v}_i,\mathbf{v}_j\rangle$和$\langle\mathbf{v}_i,\mathbf{v}_k\rangle$，它们都可以用来学习$v_i$，更一般的，包含$x_ix_j\ne0\Andi\nej$的所有样本都能用来学习$v_i$，很大程度上避免了数据稀疏性的影响。

此外，复杂度可以从$O(kd^2)$优化到$O(kd)$：

$$\begin{aligned}
&\sum_{i=1}^d\sum_{j=i+1}^d\langle\mathbf{v}_i,\mathbf{v}_j\rangle x_ix_j\\=& \frac{1}{2}\sum_{i=1}^d\sum_{j=1}^d\langle\mathbf{v}_i,\mathbf{v}_j\rangle x_ix_j-\frac{1}{2}\sum_{i=1}^d\langle\mathbf{v}_i,\mathbf{v}_j\rangle x_ix_i\\
=& \frac{1}{2}\sum_{i=1}^d\sum_{j=1}^d\sum_{f=1}^k v_{i,f}v_{j,f}x_ix_j-\frac{1}{2}\sum_{i=1}^d\sum_{f=1}^k v_{i,f}v_{i,f}x_ix_i\\
=& \frac{1}{2}\sum_{f=1}^k((\sum_{i=1}^d v_{i,f}x_i)(\sum_{j=1}^d v_{j,f}x_j)-\sum_{i=1}^d v_{i,f}^2x_i^2)\\
=& \frac{1}{2}\sum_{f=1}^k((\sum_{i=1}^d v_{i,f}x_i)^2-\sum_{i=1}^d v_{i,f}^2x_i^2)
\end{aligned}$$

可以看出，FM模型可以在线性的时间做出预测。

FM模型学习

把上述两公式合并，得到等价的FM模型公式：

$$\hat y(\mathbf{x})=w_0+\sum_{i=1}^d w_ix_i+\frac{1}{2}\sum_{f=1}^k((\sum_{i=1}^d v_{i,f}x_i)^2–\sum_{i=1}^d v_{i,f}^2x_i^2)$$

FM模型可以使用梯度下降法进行学习，模型的梯度为：

$$\frac{\partial}{\partial\theta}y(\mathbf{x})=\{\begin{array}{ll}1,&\text{if}\;\theta\;\text{is}\;w_0\\x_i,&\text{if}\;\theta\;\text{is}\;w_i\\x_i\sum_{j=1}^d v_{j,f}x_j–v_{i,f}x_i^2,&\text{if}\;\theta\;\text{is}\;v_{i,f}\end{array}$$

式中，$\sum_{j=1}^d v_{j,f}x_j$只与$f$有关而与$i$无关，在每次迭代过程中，可以预先对所有$f$的$\sum_{j=1}^d v_{j,f}x_j$进行计算，复杂度$O(kd)$，就能在常数时间$O(1)$内得到$v_{i,f}$的梯度。而对于其它参数$w_0$和$w_i$，显然也是在常数时间内计算梯度。此外，更新参数只需要$O(1)$,一共有$1+d+kd$个参数，因此FM参数训练的复杂度也是$O(kd)$。所以说，FM模型是一种高效的模型，是线性时间复杂度的，可以在线性的时间做出训练和预测。

FM总结

FM的优势

• FM降低了因数据稀疏，导致交叉项参数学习不充分的影响。直接用one-hot进行多项式建模，DataSet中没有出现的特征组合的权重是学不出来的，而FM是基于MF的思想或者说是基于latent factor model的思想进行的“曲线救国”：
  • 通过先学习每个特征的隐向量，然后通过隐向量之间的内积来刻画交互项的权重。
  • 一个组合特征的样本数一定比单特征的样本数少<=>直接学习交互项的特征一定比学习隐向量要难。且学习隐向量可以避免因数据稀疏导致的学习不充分的缺点。
• FM提升了参数学习效率，因为FM需要训练的参数更少，一般情况下，隐向量的维度都是比较短的，且肯定原小于直接学习交互项的参数个数。
• FM模型对稀疏数据有更好的学习能力，通过交互项可以学习特征之间的关联关系，并且保证了学习效率和预估能力。
• 与其他模型相比，它的优势如下：
  • FM是一种比较灵活的模型，通过合适的特征变换方式，FM可以模拟二阶多项式核的SVM模型、MF模型、SVD++模型等；
  • 相比SVM的二阶多项式核而言，FM在样本稀疏的情况下是有优势的；而且，FM的训练/预测复杂度是线性的，而二项多项式核SVM需要计算核矩阵，核矩阵复杂度就是N平方。
  • MF虽然可以用类似SVD++等方式来增强对交互特征的学习，但是最多只能加两个特征。而FM是可以对任意阶的所有交互项进行学习
• FM能玩得通的一些巧妙性：
  • FM求解latent factor vector的套路，是基于MF的latent factor model方法来做。
  • 矩阵分解大法用在FM上，以缩减参数个数，处理数据稀疏带来的学习不足问题，还能做embedding；
  • FM可以看做是MF的generalized版本，不仅能够利用普通的用户反馈信息，还能融合情景信息、社交信息等诸多影响个性化推荐的因素。

SVM和FM的区别

• SVM的二元特征交叉参数是独立的，而FM的二元特征交叉参数是两个k维的向量$v_i$、$v_j$，交叉参数就不是独立的，而是相互影响的。
• FM可以在原始形式下进行优化学习，而基于kernel的非线性SVM通常需要在对偶形式下进行
• FM的模型预测是与训练样本独立，而SVM则与部分训练样本有关，即支持向量

为什么线性SVM在和多项式SVM在稀疏条件下效果会比较差呢？线性svm只有一维特征，不能挖掘深层次的组合特征在实际预测中并没有很好的表现；而多项式svn正如前面提到的，交叉的多个特征需要在训练集上共现才能被学习到，否则该对应的参数就为0，这样对于测试集上的case而言这样的特征就失去了意义，因此在稀疏条件下，SVM表现并不能让人满意。而FM不一样，通过向量化的交叉，可以学习到不同特征之间的交互，进行提取到更深层次的抽象意义。

FM和LR的区别

• LR是从组合特征的角度去描述单特征之间的交互组合；FM实际上是从模型（latent factor model）的角度来做的。即FM中特征的交互是模型参数的一部分。
• FM能很大程度上避免了数据系数行造成参数估计不准确的影响。
• FM是通过MF的思想，基于latent factor，来降低交叉项参数学习不充分的影响
  • 具体而言，两个交互项的参数学习，是基于K维的latent factor
  • 每个特征的latent factor是通过它与其它(n-1)个特征的latent factor交互后进行学习的，这就大大的降低了因稀疏带来的学习不足的问题。
  • latent factor学习充分了，交互项（两个latent factor之间的内积）也就学习充分了。
  • 即FM学习的交互项的参数是单特征的隐向量。

FFM

FFM是NTU（国立台湾大学）的 Yu-Chin Juan（阮毓钦，现在美国 Criteo 工作）与其比赛队员，借鉴了来自 Michael Jahrer 的论文中的 field 概念提出了 FM 的升级版模型。

考虑下面的数据集：

对于第一条数据来说，FM 模型的二次项为：${\bf w}_{EPSN}\cdot{\bf w}_{Nike}+{\bf w}_{EPSN}\cdot{\bf w}_{Male}+{\bf w}_{Nike}\cdot{\bf w}_{Male}$。每个特征只用一个隐向量来学习和其它特征的潜在影响。对于上面的例子中，Nike 是广告主，Male 是用户的性别，描述（EPSN，Nike）和（EPSN，Male）特征组合，FM 模型都用同一个 $w_{ESPN}$，而实际上，ESPN 作为广告商，其对广告主和用户性别的潜在影响可能是不同的。

因此，Yu-Chin Juan 借鉴 Michael Jahrer 的论文Ensemble of collaborative filtering and feature engineered models for click through rate prediction，将 field 概念引入 FM 模型。

field 是什么呢？即相同性质的特征放在一个 field。比如 EPSN、NBC 都是属于广告商 field 的，Nike、Adidas 都是属于广告主 field，Male、Female 都是属于性别 field 的。简单的说，同一个类别特征进行 one-hot 编码后生成的数值特征都可以放在同一个 field 中，比如最开始的例子中 Day=26/11/15 Day=19/2/15 可以放于同一个 field 中。如果是数值特征而非类别，可以直接作为一个 field。

引入了 field 后，对于刚才的例子来说，二次项变为：

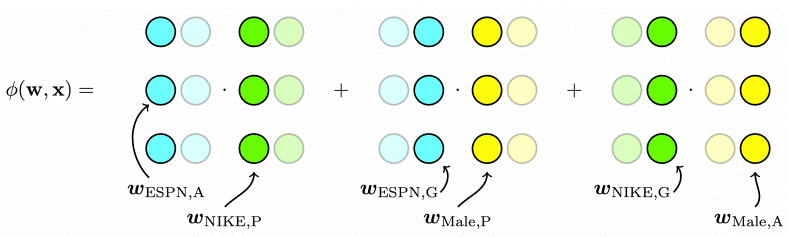
$$\underbrace{{\bf w}_{EPSN,A}\cdot{\bf w}_{Nike,P}}_{P\times A}+\underbrace{{\bf w}_{EPSN,G}\cdot{\bf w}_{Male,P}}_{P\times G}+\underbrace{{{\bf w}_{Nike,G}\cdot{\bf w}_{Male,A}}}_{A\times G}$$

• 对于特征组合（EPSN，Nike）来说，其隐向量采用的是 $w_{EPSN,A}$ 和 $w_{Nike,P}$，对于 $w_{EPSN,A}$ 这是因为 Nike 属于广告主（Advertiser）的 field，而第二项 w_{Nike,P} 则是 EPSN 是广告商（Publisher）的 field。
• 对于特征组合（EPSN，Male）来说，$w_{EPSN,G}$ 是因为 Male 是用户性别(Gender)的 field，而第二项 $w_{Male,P}$ 是因为 EPSN 是广告商（Publisher）的 field。

下面的图来很好的表示了三个模型的区别：

• For Poly2, a dedicated weight is learned for each feature pair:

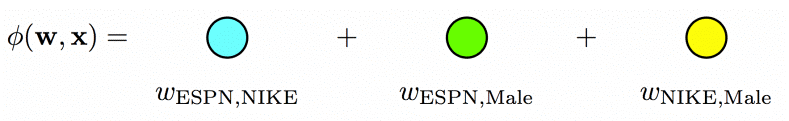
• For FMs, each feature has one latent vector, which is used to interact with any other latent vectors:

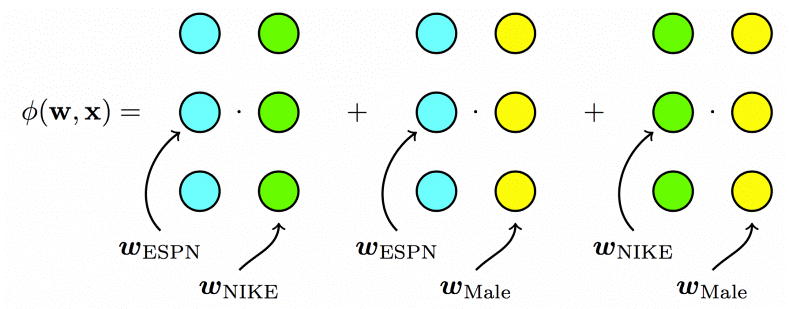
• For FFMs, each feature has several latent vectors, one of them is used depending on the field of the other feature:

FFM 数学公式

因此，FFM 的数学公式表示为：

$$y(\mathbf{x})=w_0+\sum_{i=1}^dw_ix_i+\sum_{i=1}^d\sum_{j=i+1}^d(w_{i,f_j}\cdot w_{j,f_i})x_ix_j$$

$f_i$ 和 $f_j$ 分别代表第 i 个特征和第 j 个特征所属的 field。若 field 有 f 个，隐向量的长度为 k，则二次项系数共有 $dfk$ 个，远多于 FM 模型的 dk 个。此外，隐向量和 field 相关，并不能像 FM 模型一样将二次项化简，计算的复杂度是 $d^2k$。

通常情况下，每个隐向量只需要学习特定 field 的表示，所以有 $k_{FFM}\ll k_{FM}$。

FFM 模型学习

为了方便推导，这里省略FFM的一次项和常数项，公式为：

$$\phi(\mathbf{w},\mathbf{x})=\sum_{a=1}^d\sum_{b=a+1}^d(w_{a,f_b}\cdot w_{b,f_a})x_ax_b$$

FFM模型使用logistic loss作为损失函数，并加上L2正则项：

$$\mathcal{L}=\sum_{i=1}^N\log\left(1+\exp(-y_i\phi({\bf w},{\bf x_i}))\right)+\frac{\lambda}{2}|\!|{\bf w}|\!|^2$$

采用随机梯度下降来（SGD）来优化损失函数，因此，损失函数只采用单个样本的损失：

$$\mathcal{L}=\log\left(1+\exp(-y_i\phi({\bf w},{\bf x}))\right)+\frac{\lambda}{2}|\!|{\bf w}|\!|^2$$

对于每次迭代，选取一条数据$(x,y)$，然后让L对$w_{a,f_b}$和$w_{b,f_a}$求偏导（注意，采用SGD上面的求和项就去掉了，只采用单个样本的损失），得：

$$g_{a,f_b}\equiv\frac{\partial\mathcal{L}}{\partial w_{a,f_b}}=\kappa\cdot w_{b,f_a}x_ax_b+\lambda w_{a,f_b}^2$$

$$g_{b,f_a}\equiv\frac{\partial\mathcal{L}}{\partial w_{b,f_a}}=\kappa\cdot w_{a,f_b}x_ax_b+\lambda w_{b,f_a}^2$$

其中，$\kappa=\frac{-y}{1+\exp(y\phi({\bf w,x}))}$

在具体的实现中，这里有两个trick，第一个trick是梯度的分步计算。

$$\mathcal{L}=\mathcal{L}_{err}+\mathcal{L}_{reg}=\log\left(1+\exp(-y_i\phi({\bf w},{\bf x}))\right)+\frac{\lambda}{2}|\!|{\bf w}|\!|^2$$

$$\frac{\partial\mathcal{L}}{\partial\mathbf{w}}=\frac{\partial\mathcal{L}_{err}}{\partial\phi}\cdot\frac{\partial\phi}{\partial\mathbf{w}}+\frac{\partial\mathcal{L}_{reg}}{\partial\mathbf{w}}$$

注意到$\frac{\partial\mathcal{L}_{err}}{\partial\phi}$和参数无关，每次更新模型时，只需要计算一次，之后直接调用结果即可。对于总共有$dfk$个模型参数的计算来说，使用这种方式能极大提升运算效率。

第二个trick是FFM的学习率是随迭代次数变化的，具体的是采用AdaGrad算法。Adagrad算法能够在训练中自动的调整学习率，对于稀疏的参数增加学习率，而稠密的参数则降低学习率。因此，Adagrad非常适合处理稀疏数据。

设$g_{t,j}$第t轮第j个参数的梯度，则SGD和采用Adagrad的参数更新公式分别如下：

$$SGD: w_{t+1,j}=w_{t,j}-\eta\cdot g_{t,j}$$

$$Adagrad: w_{t+1,j}=w_{t,j}–\frac{\eta}{\sqrt{G_{t,jj}+\epsilon}}\cdot g_{t,j}$$

可以看出，Adagrad在学习率η上还除以一项$\sqrt{G_{t,jj}+\epsilon}$，这是什么意思呢？$\epsilon$为平滑项，防止分母为0，$G_{t,jj}=\sum_{\iota=1}^tg_{\iota,jj}^2$即$G_{t,jj}$为对角矩阵，每个对角线位置$j,j$的值为参数$w_j$每一轮的平方和，可以看出，随着迭代的进行，每个参数的历史梯度累加到一起，使得每个参数的学习率逐渐减小。

因此，用3-5、3-6计算完梯度后，下一步就是更新分母的对角矩阵：

$$G_{a,f_b}\leftarrow G_{a,f_b}+(g_{a,f_b})^2$$

$$G_{b,f_a}\leftarrow G_{b,f_a}+(g_{b,f_a})^2$$

最后，更新模型参数：

$$w_{a,f_b}\leftarrow w_{a,f_b}–\frac{\eta}{\sqrt{G_{a,f_b}+1}}g_{a,f_b}$$

$$w_{b,f_a}\leftarrow w_{b,f_a}–\frac{\eta}{\sqrt{G_{b,f_a}+1}}g_{b,f_a}$$

这就是论文中算法1描述的过程：

FFM使用技巧

在FFM原论文中，作者指出，FFM模型对于one-hot后类别特征十分有效，但是如果数据不够稀疏，可能相比其它模型提升没有稀疏的时候那么大，此外，对于数值型的数据效果不是特别的好。在Github上有FFM的开源实现，要使用FFM模型，特征需要转化为“field_id:feature_id:value”格式，相比LibSVM的格式多了field_id，即特征所属的field的编号，feature_id是特征编号，value为特征的值。

此外，美团点评的文章中，提到了训练FFM时的一些注意事项：

• 样本归一化。FFM默认是进行样本数据的归一化的。若不进行归一化，很容易造成数据inf溢出，进而引起梯度计算的nan错误。因此，样本层面的数据是推荐进行归一化的。
• 特征归一化。CTR/CVR模型采用了多种类型的源特征，包括数值型和categorical类型等。但是，categorical类编码后的特征取值只有0或1，较大的数值型特征会造成样本归一化后categorical类生成特征的值非常小，没有区分性。例如，一条用户-商品记录，用户为“男”性，商品的销量是5000个（假设其它特征的值为零），那么归一化后特征“sex=male”（性别为男）的值略小于0002，而“volume”（销量）的值近似为1。特征“sex=male”在这个样本中的作用几乎可以忽略不计，这是相当不合理的。因此，将源数值型特征的值归一化到[0,1]是非常必要的。
• 省略零值特征。从FFM模型的表达式(3-1)可以看出，零值特征对模型完全没有贡献。包含零值特征的一次项和组合项均为零，对于训练模型参数或者目标值预估是没有作用的。因此，可以省去零值特征，提高FFM模型训练和预测的速度，这也是稀疏样本采用FFM的显著优势。

DeepFM

近年来深度学习模型在解决NLP、CV等领域的问题上取得了不错的效果，于是有学者将深度神经网络模型与FM模型结合，提出了DeepFM模型。FM通过对于每一位特征的隐变量内积来提取特征组合，最后的结果也不错，虽然理论上FM可以对高阶特征组合进行建模，但实际上因为计算复杂度原因，一般都只用到了二阶特征组合。对于告诫特征组合来说，我们很自然想到多层神经网络DNN。

FM的结构

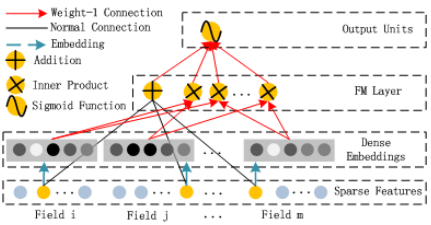
DNN结构

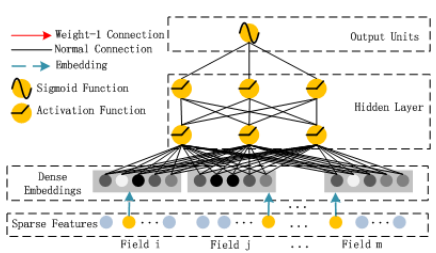
DeepFM结构（FM和DNN的特征结合）

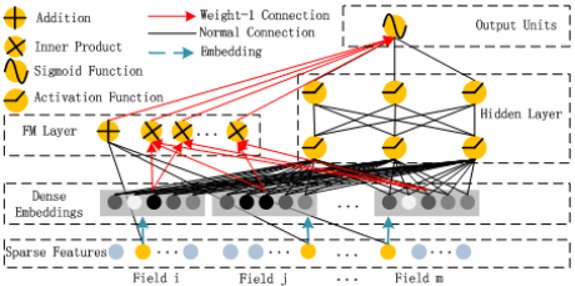
DeepFM的架构其实特别清晰:

• 输入的是稀疏特征的id

进行一层 lookup 之后得到 id 的稠密 embedding

• 这个 embedding 一方面作为隐向量输入到 FM 层进行计算
• 同时该 embedding 进行聚合之后输入到一个 DNN 模型 (deep)
• 然后将 FM 层和 DNN 层的输入求和之后进行 co-train

DeepFM 目的是同时学习低阶和高阶的特征交叉，主要由 FM 和 DNN 两部分组成，底部共享同样的输入。模型可以表示为：

$$\hat{y}=sigmoid(y_{FM}+y_{DNN})$$

FM 部分

原理如上，数学表达为：

$$y_{FM}=<w,x>+\sum_{i=1}^d\sum_{j=i+1}^d<V_i,V_j>x_i\cdot x_j$$

Deep 部分

深度部分是一个前馈神经网络，与图像或语音类的输入不同，CTR 的输入一般是极其稀疏的，因此需要重新设计网络结构。在第一层隐藏层之前，引入一个嵌入层来完成输入向量压缩到低位稠密向量：

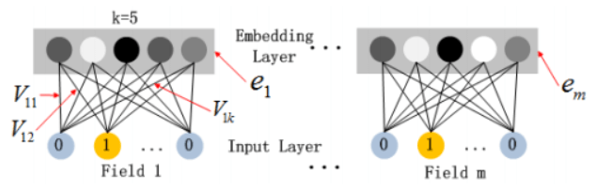
嵌入层的结构如上图所示，有两个有趣的特性：

• 尽管不同 field 的输入长度不同，但是 embedding 之后向量的长度均为 k
• 在 FM 中得到的隐变量 $V_{ik}$ 现在作为嵌入层网络的权重

嵌入层的输出为 $a^{(0)}=[e_1,e_2,…,e_m]$，其中 $e_i$ 是嵌入的第 i 个 filed，m 是 field 的个数，前向过程将嵌入层的输出输入到隐藏层为：

$$a^{(l+1)}=\sigma(W^{(l)}a^{(l)}+b^{(l)})$$

其中 l 是层数，$\sigma$ 是激活函数，$W^{(l)}$ 是模型的权重，$b^{(l)}$ 是 l 层的偏置，因此，DNN 得预测模型表达为：

$$y_{DNN}=W^{|H|+1}\cdot a^{|H|}+b^{|H|+1}$$

其中，$|H|$ 为隐藏层层数。

DeepFM 模型对比

目前在推荐领域中比较流行的深度模型有 FNN、PNN、Wide&Deep。

• FNN 模型是用 FM 模型来对 Embedding 层进行初始化的全连接神经网络。
• PNN 模型则是在 Embedding 层和全连接层之间引入了内积/外积层，来学习特征之间的交互关系。
• Wide&Deep 模型由谷歌提出，将 LR 和 DNN 联合训练，在 Google Play 取得了线上效果的提升。Wide&Deep 模型，很大程度上满足了模型同时学习低阶特征和高阶特征的需求，让模型同时具备较好的“memorization”和“generalization”。但是需要人工特征工程来为 Wide 模型选取输入特征。具体而言，对哪些稀疏的特征进行 embedding，是由人工指定的。

有学者将 DeepFM 与当前流行的应用于 CTR 的神经网络做了对比：

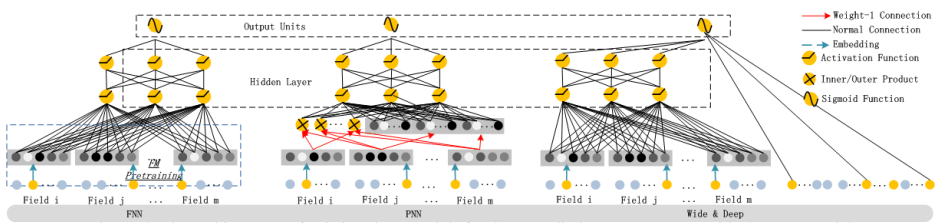
从预训练，特征维度以及特征工程的角度进行对比，发现：

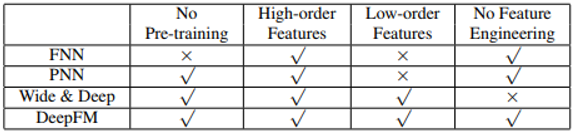
从实验效果来看，DeepFM 的效果较好：

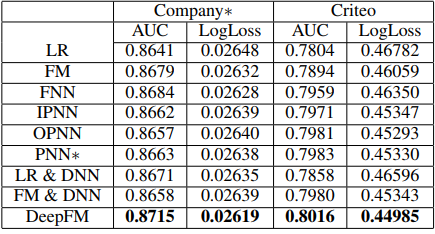
DeepFM 的三大优势：

• 相对于 Wide&Deep 不再需要手工构建 wide 部分；
• 相对于 FNN 把 FM 的隐向量参数直接作为网络参数学习；
• DeepFM 将 embedding 层结果输入给 FM 和 MLP，两者输出叠加，达到捕捉了低阶和高阶特征交叉的目的。

NFM (Neural Factorization Machines)

NFM (Neural Factorization Machines) 又是在 FM 上的一个改进工作，出发点是 FM 通过隐向量可以对完成一个很好的特征组合工作，并且还解决了稀疏的问题，但是 FM 对于它对于 non-linear 和 higher-order 特征交叉能力不足，而 NFM 则是结合了 FM 和 NN 来弥补这个不足。

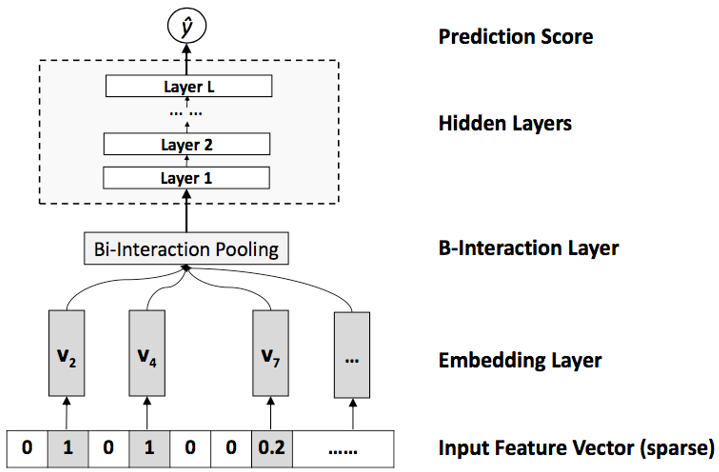
DeepFM 是用 Wide&Deep 框架，在 FM 旁边加了一个 NN，最后一并 sigmoid 输出。NFM 的做法则是利用隐向量逐项相乘得到的向量作为 MLP 的输入，构建的 FM+NN 模型。其中：

• Input Feature Vector 层是输入的稀疏向量，可以带权
• Embedding Layer 对输入的稀疏向量 lookup 成稠密的 embedding 向量
• Bi-Interaction Layer 将每个特征 embedding 进行两两做 element-wise product，Bi-Interaction 的输出是一个 k 维向量（就是隐向量的大小）,这层负责了特征之间 second-order 组合。$f_{\text{Bi}}(V_x)=\sum_i^n\sum_{j=i+1}^nx_iv_i\odot x_jv_j$ 类似 FM 的式子转换，这里同样可以做如下转换将复杂度降低：$f_{\text{Bi}}(V_x)=\frac{1}{2}\left[(\sum_i^nx_iv_i)^2-\sum_i^n(x_iv_i)^2\right]$
• Hidden Layers 这里是多层学习高阶组合特征学习,其实就是一个 DNN 模块:$z_1=\sigma_1(W_1f_{\text{Bi}}(V_x)+b_1)\\z_2=\sigma_2(W_2z_1+b_2)\\…\\z_L=\sigma_L(W_Lz_{L-1}+b_L)$
• Prediction Score 层就是输出最终的结果：$y_{\text{NFM}}(x)=w_0+\sum_i^nw_ix_i+h^T\sigma_L(W_l(…\sigma_1(W_1f_{\text{Bi}}(V_x)+b_1))+b_L)$

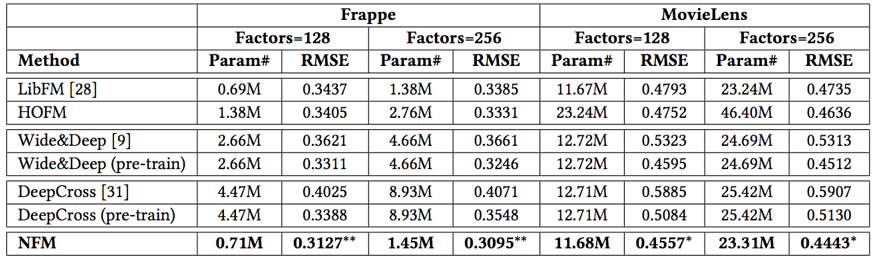
FM 可以看做是 NFM 模型 Hidden Layer 层数为 0 一种特殊形式。最终的实验效果看来 NFM 也还是可以带来一个不错的效果：

AFM (Attentional Factorization Machines)

AFM (Attentional Factorization Machines)是浙大（Jun Xiao, Hao Ye, Fei Wu）和新加坡国大（Xiangnan He, Hanwang Zhang, Tat-Seng Chua）几位同学提出来的模型。AFM首先对FM做了神经网络改造，而后加入了注意力机制，为不同特征的二阶组合分配不同的权重。在传统的FM中进行特征组合时两两特征之间的组合都是等价的(只能通过隐向量的点积来区别)，这里趁着Attention的热度走一波，因为AFM的最大的贡献就是通过Attention建立权重矩阵来学习两两向量组合时不同的权重。下面就是AFM的框架图：

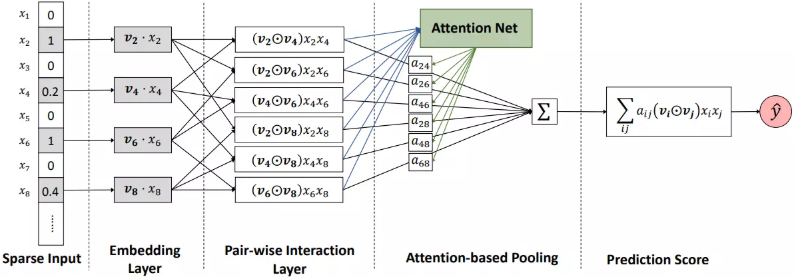
从图中可以很清晰的看出,AFM比FM就是多了一层Attention-based Pooling，该层的作用是通过Attention机制生成一个$\alpha_{ij}$权重矩阵，该权重矩阵将会作用到最后的二阶项中，因此这里$\alpha_{ij}$的生成步骤是先通过原始的二阶点积求得各自的组合的一个Score：

$${a}’_{i,j}=h^T\text{ReLu}(W(v_i\odot v_j)x_ix_j+b)$$

其中$W\in\mathbb{R}^{t\times k},b\in\mathbb{R}^t,h\in\mathbb{R}^t$，这里t表示Attention网络的大小。然后对其score进行softmax的归一化：

$$a_{i,j}=\frac{exp({a}’_{i,j})}{\sum_{i,j}exp({a}’_{i,j})}$$

最后该权重矩阵再次用于二阶项的计算（也就是最终的AFM式子）：

$$\hat y=f(\vec x)=w_0+\sum_{i=1}^{n}w_ix_i+\sum_{0<i<j<=n}\alpha_{ij}\big\langle\vec p,(\vec v_i\odot\vec v_j)\big\rangle x_ix_j.$$

这里，$\alpha_{ij}$是通过注意力机制学习得到的特征$i$和特征$j$组合的权重，$\vec p$是对隐向量每个维度学习得到的权重，$\vec v_i\odot\vec v_j$表示向量$\vec v_i$和$\vec v_j$逐项相乘得到的新向量。显然，当$\alpha_{ij}\equiv1$且$\vec p=\vec 1$时，AFM退化为标准的FM模型。

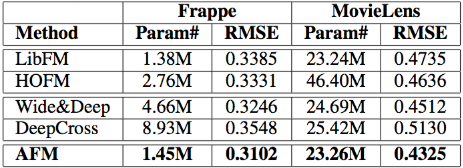
其实整个算法思路也是很简单，但是在实验上却有一个不错的效果：

参考链接：

• 深入FFM原理与实践
• 『我爱机器学习』FM、FFM与DeepFM
• CTR预估算法之FM,FFM,DeepFM及实践
• FM系列算法解读（FM+FFM+DeepFM）
• 深入浅出FM和类似推荐算法
• 综述：机器学习在CTR中的应用
• 基于深度学习的ctr预估模型集合