时序预测模型 Uber Orbit

UberOrbit简介

Uber开源的Orbit是一个专为时间序列预测设计的Python库，旨在帮助开发者快速构建、评估和部署预测模型。它结合了统计模型和机器学习技术，特别适合处理具有复杂季节性、趋势性和外部协变量的时间序列数据。

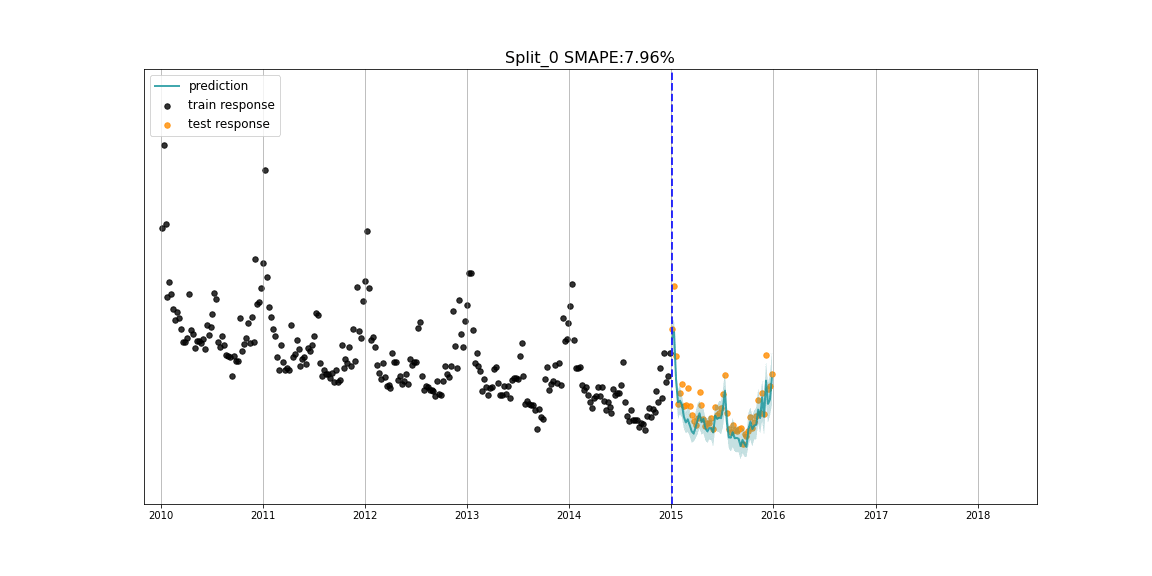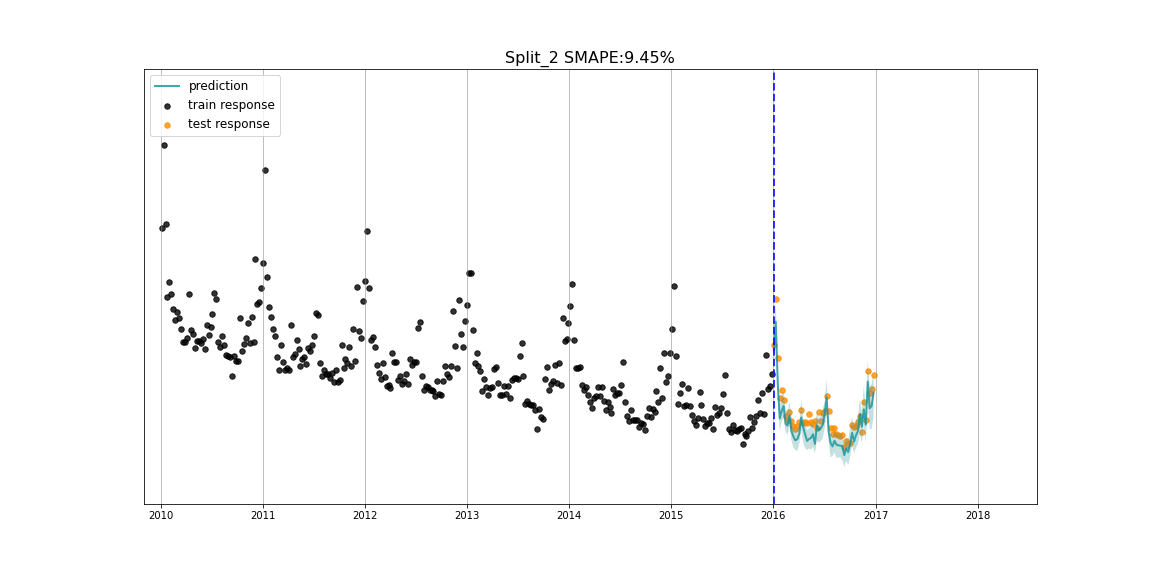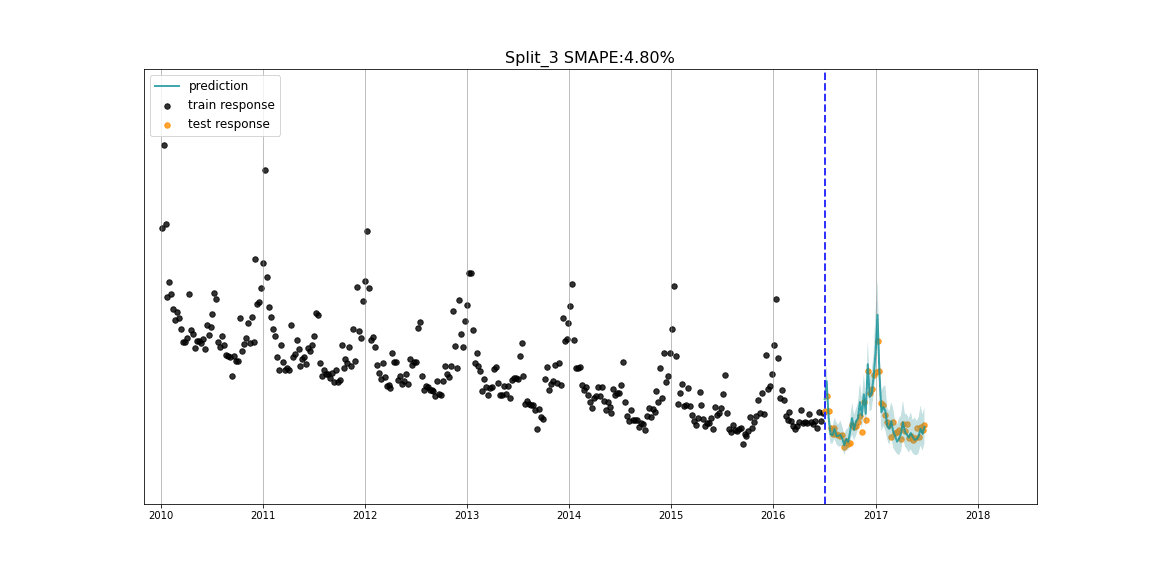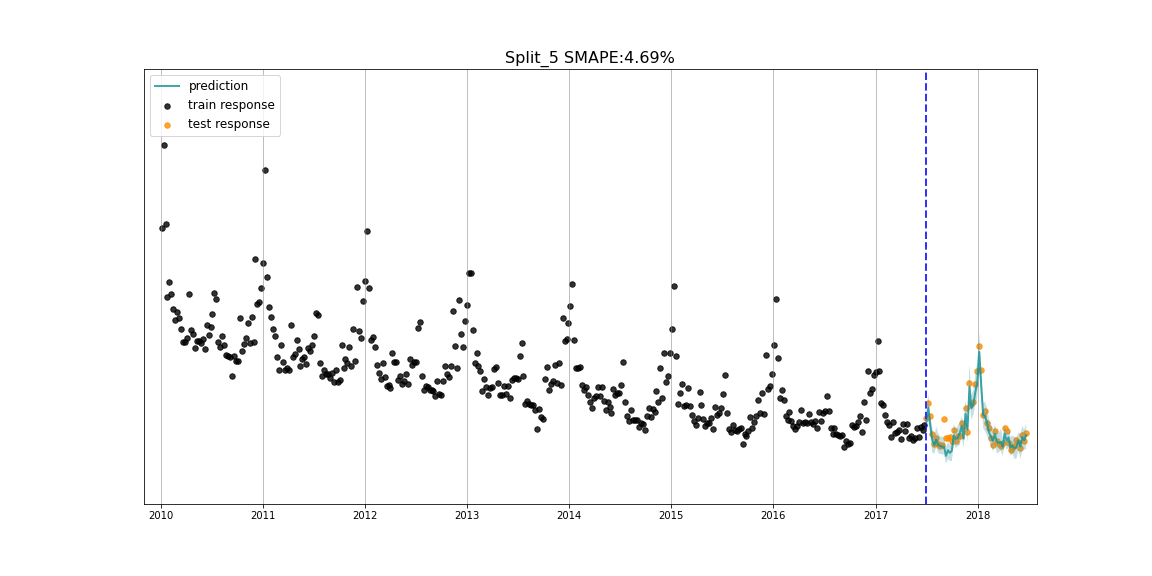
核心功能

• 多模型支持：提供多种预测模型，包括：
  • Prophet（基于加性模型的经典时间序列预测）
  • ETS（指数平滑）
  • LGT（基于贝叶斯推断的灵活模型，支持局部全局趋势和季节性）
  • DGLM（动态广义线性模型，适用于非线性趋势和离散数据）
• 贝叶斯推断：利用PyStan或Pyro进行概率建模，支持不确定性量化。
• 自动特征工程：自动处理节假日、季节性和外部协变量（如促销活动、天气数据）。
• 可解释性：提供模型参数的可视化和解释工具。
• 生产就绪：支持模型序列化和部署。

架构设计

• 模块化结构：
  • Model：定义模型类型（如LGT、DGLM）及参数。
  • Estimator：拟合模型（支持MCMC或MAP推断）。
  • Predictor：生成预测结果及置信区间。
• 后端引擎：支持Stan（默认）或Pyro（用于深度学习扩展）。
• 可视化工具：内置绘图函数，用于分析趋势、季节性和预测结果。

适用场景

• 业务预测：如需求预测（打车订单、商品销量）、资源调度。
• 异常检测：通过预测区间识别异常值。
• 因果推断：分析外部变量（如政策变化）对时间序列的影响。

优势与局限

• 优势：
  • 灵活性：支持从传统统计模型到贝叶斯深度学习。
  • 易用性：API简洁，适合快速原型开发。
  • 可解释性：提供趋势、季节性和协变量影响的直观分析。
• 局限：
  • 计算资源：贝叶斯方法（如MCMC）可能较慢，不适合超大规模数据。
  • 模型选择：需手动选择模型类型，缺乏全自动的AutoML功能。

对比其他工具

• vs Facebook Prophet：Orbit支持更多模型（如LGT/DGLM）和贝叶斯推断。
• vs statsmodels/ETS：提供更现代化的接口和协变量集成。
• vs Pyro/Stan原生代码：Orbit封装了底层复杂性，适合快速开发。

UberOrbit使用教程

安装与环境配置

安装Orbit

# 安装最新版本（推荐使用Python 3.8+）
pip install orbit-ml

• 主要依赖：NumPy、pandas、Matplotlib、PyStan/Pyro。
• 可选依赖：TensorFlow Probability（用于高级模型）。

安装后端依赖

Orbit支持Stan（默认）或Pyro作为推断引擎：

# 安装PyStan（默认，适用于大多数场景）
pip install pystan

# 或安装Pyro（支持贝叶斯深度学习）
pip install pyro-ppl

数据准备

数据格式要求

• 必需列：date（日期时间列）和response（目标变量列）。
• 可选列：外部协变量（如促销活动、天气数据）。

生成示例数据

使用Orbit内置工具生成时间序列数据：

from orbit.datasets import generate_ts_data

# 生成数据：24小时季节性，线性趋势
df = generate_ts_data(
seasonality=24,
trend_order=1,
noise_scale=0.1,
n_obs=500,
freq="H" # 每小时频率
)
print(df.head())

加载自定义数据

import pandas as pd

# 示例：加载CSV数据（需包含日期列和目标列）
df = pd.read_csv("your_data.csv")
df["date"] = pd.to_datetime(df["date"]) # 确保日期格式正确

模型训练

选择模型类型

Orbit提供多种模型：

• LGT（局部全局趋势模型，适合复杂季节性）
• DGLM（动态广义线性模型，支持非线性趋势）
• Prophet（类似Facebook Prophet）

训练示例：LGT模型

from orbit.models import LGT
from orbit.diagnostics.backtest import TimeSeriesSplit

# 分割训练集和测试集
df_train, df_test = df[:-100], df[-100:]

# 初始化模型（使用MCMC推断）
model = LGT(
response_col="response",
date_col="date",
seasonality=24, # 指定季节性周期
seed=42, # 随机种子
estimator="stan-mcmc", # 使用MCMC推断（支持"stan-map"或"pyro-svi"）
n_bootstrap_draws=1000 # 采样数量
)

# 训练模型
model.fit(df=df_train)

# 查看模型参数
print(model.get_post_params())

快速推断（MAP）

若数据量大或需要快速原型开发，使用最大后验估计（MAP）：

model = LGT(
    response_col = "response",
    date_col = "date",
    seasonality = 24,
    estimator = "stan-map" # 快速推断
)
model.fit(df_train)

预测与评估

生成预测结果

# 预测未来100个时间点
predicted = model.predict(df = df_test)

# 输出预测结果（包括均值、置信区间）
print(predicted.head())

评估指标

计算MAE、RMSE等指标：

from orbit.diagnostics.metrics import smape, wmape

# 计算SMAPE和WMAPE
smape_score = smape(df_test["response"], predicted["prediction"])
wmape_score = wmape(df_test["response"], predicted["prediction"])
print(f"SMAPE: {smape_score:.2f}%, WMAPE: {wmape_score:.2f}%")

可视化

绘制预测结果

model.plot_predict(
    predicted = predicted,
    actuals = df_test,
    figsize = (14, 6),
    title = "LGT模型预测结果"
)

分解趋势和季节性

# 查看模型组件（趋势、季节性和协变量影响）
model.plot_components(
    predicted = predicted,
    figsize = (14, 8),
    plots = ["trend", "seasonality", "components"]
)

高级功能

添加节假日效应

from orbit.features import get_event_prediction

# 定义节假日日期
holidays = pd.DataFrame({
    "date": ["2023-01-01", "2023-12-25"],
    "holiday_name": ["NewYear", "Christmas"]
})

# 生成节假日特征
df = get_event_prediction(
    df = df,
    date_col = "date",
    event_df = holidays,
    event_name_col = "holiday_name"
)

# 在模型中添加节假日协变量
model = LGT(
    response_col = "response",
    date_col = "date",
    seasonality = 24,
    extra_seasonalities = [{"name": "yearly", "period": 365.25, "order": 3}],
    regressor_col = ["holiday_NewYear", "holiday_Christmas"] # 添加节假日列
)

使用Pyro后端（深度学习）

from orbit.models import DGLM

# 使用Pyro的随机变分推断（SVI）
model = DGLM(
    response_col = "response",
    date_col = "date",
    estimator = "pyro-svi",
    learning_rate = 0.1,
    num_steps = 1000
)
model.fit(df_train)

模型保存与加载

保存模型

import orbit

# 保存为文件
orbit.utils.serialize_pickle(model, "model.pkl")

加载模型

model = orbit.utils.deserialize_pickle("model.pkl")
predicted = model.predict(df_test)

注意事项

• 数据频率：确保数据频率（如小时、天）与seasonality参数一致。
• 计算资源：MCMC方法较慢，建议在GPU上使用Pyro加速。
• 版本兼容性：检查orbit-ml和pystan/pyro版本是否匹配。
• 缺失值处理：Orbit不支持自动处理缺失值，需提前填充或删除。

UberOrbit自动特征工程

自动处理节假日

节假日特征生成逻辑

Orbit通过get_event_prediction函数将原始日期数据转换为节假日特征矩阵。其核心流程如下：

输入数据结构

• 原始数据：需包含日期列（date_col）。
• 节假日定义表：至少包含两列：
  • date：节假日的具体日期（如”2023-01-01″）。
  • holiday_name：节假日名称（如”NewYear”）。

特征生成步骤

• 日期对齐：将节假日日期与原始数据日期对齐。
• 窗口效应：为每个节假日生成前后影响期的标志。例如，event_window=2表示节假日当天及前后各1天（共3天）会被标记为影响期。
• 特征编码：生成二元（0/1）特征列，格式为holiday_<holiday_name>。示例：holiday_NewYear列在影响期内为1，否则为0。

生成示例

from orbit.features import get_event_prediction
import pandas as pd

# 原始数据（假设按天频率）
df = pd.DataFrame({
    "date": pd.date_range(start="2023-01-01", end="2023-01-07", freq="D"),
    "response": [100, 120, 150, 200, 180, 90, 80]
})

# 定义节假日（春节影响前后各1天）
holidays_df = pd.DataFrame({
    "date": ["2023-01-02"],
    "holiday_name": ["SpringFestival"]
})

# 生成节假日特征（窗口为2天：前一天、当天、后一天）
df = get_event_prediction(
    df=df,
    date_col="date",
    event_df=holidays_df,
    event_name_col="holiday_name",
    event_window=2 # 影响天数范围：[-1,+1]
)

# 输出结果
print(df[["date", "holiday_SpringFestival"]])
输出：
date holiday_SpringFestival
0 2023-01-01 1 # 节假日前1天
1 2023-01-02 1 # 节假日当天
2 2023-01-03 1 # 节假日后1天
3 2023-01-04 0
4 2023-01-05 0
...

模型集成节假日特征

在模型中声明协变量

将生成的节假日列名传递给模型的 regressor_col 参数：

from orbit.models import LGT

model = LGT(
    response_col="response",
    date_col="date",
    regressor_col=["holiday_SpringFestival"], # 指定节假日特征
    seasonality=7, # 周季节性
    estimator="stan-mcmc"
)
model.fit(df)

模型如何利用节假日特征

• 回归系数：节假日特征作为线性回归项影响预测值。例如，holiday_SpringFestival 的系数表示该节假日对目标变量的平均影响。
• 不确定性量化：贝叶斯框架下，系数会生成后验分布，反映节假日效应的置信度。

复杂场景的设置

以下是针对春节复杂场景的 Orbit 节假日配置方案，涵盖动态放假日期、调休窗口及订单量波动模式的完整实现步骤：

场景特征拆解

假设春节对业务的影响分为三个阶段：

• 节前调休期（提前5天）：订单量逐步上升。
• 正式假期（7天）：订单量骤降。
• 节后调休期（假期后2天）：订单量回升。

例如：

• 2023年春节：假期为2023-01-21至2023-01-27，调休为2023-01-16至2023-01-20（节前）和2023-01-28至2023-01-29（节后）。
• 2024年春节：假期为2024-02-10至2024-02-17，调休为2024-02-04至2024-02-09（节前）和2024-02-18至2024-02-19（节后）。

构建春节日期表

import pandas as pd

# 定义不同年份的春节假期和调休日期（示例）
spring_festival_df = pd.DataFrame([
    {
        "year": 2023,
        "pre_start": "2023-01-16", # 节前调休开始
        "pre_end": "2023-01-20", # 节前调休结束
        "holiday_start": "2023-01-21", # 正式假期开始
        "holiday_end": "2023-01-27", # 正式假期结束
        "post_start": "2023-01-28", # 节后调休开始
        "post_end": "2023-01-29" # 节后调休结束
    },
    {
        "year": 2024,
        "pre_start": "2024-02-04",
        "pre_end": "2024-02-09",
        "holiday_start": "2024-02-10",
        "holiday_end": "2024-02-17",
        "post_start": "2024-02-18",
        "post_end": "2024-02-19"
    }
])

生成分段特征

将春节拆分为三个独立事件（节前调休、正式假期、节后调休），并为每个事件生成特征：

from orbit.features import get_event_prediction

def generate_spring_festival_features(df, spring_festival_df):
    # 生成节前调休特征
    df_pre = get_event_prediction(
        df=df,
        date_col="date",
        event_df=spring_festival_df[["pre_start", "pre_end"]],
        event_name_col=None,
        event_start_col="pre_start",
        event_end_col="pre_end",
        feature_name="spring_festival_pre"
    )

    # 生成正式假期特征
    df_holiday = get_event_prediction(
        df=df,
        date_col="date",
        event_df=spring_festival_df[["holiday_start", "holiday_end"]],
        event_name_col=None,
        event_start_col="holiday_start",
        event_end_col="holiday_end",
        feature_name="spring_festival_holiday"
    )

    # 生成节后调休特征
    df_post = get_event_prediction(
        df=df,
        date_col="date",
        event_df=spring_festival_df[["post_start", "post_end"]],
        event_name_col=None,
        event_start_col="post_start",
        event_end_col="post_end",
        feature_name="spring_festival_post"
    )

    # 合并所有特征
    df = pd.concat([df, df_pre[[f"event_spring_festival_pre"]],
                   df_holiday[[f"event_spring_festival_holiday"]],
                   df_post[[f"event_spring_festival_post"]]], axis=1)
    return df

# 生成特征（假设 df 是原始数据）
df = generate_spring_festival_features(df, spring_festival_df)

定义动态影响模式

根据业务逻辑，为不同阶段设置不同的影响方向：

• 节前调休期（spring_festival_pre）：正向影响（订单量上升）。
• 正式假期（spring_festival_holiday）：负向影响（订单量下降）。
• 节后调休期（spring_festival_post）：正向影响（订单量回升）。

模型初始化

from orbit.models import LGT

model = LGT(
    response_col="orders",
    date_col="date",
    regressor_col=[
        "event_spring_festival_pre",
        "event_spring_festival_holiday",
        "event_spring_festival_post"
    ],
    seasonality=365.25,  # 年季节性
    estimator="stan-mcmc",
    regressor_sigma_prior=[0.5, 0.5, 0.5]  # 约束系数范围（根据业务调整）
)
model.fit(df)

高级配置（非线性影响）

若订单量在节前调休期呈渐进上升（非线性），可使用衰减函数调整特征权重。

自定义节前调休特征

from orbit.features import EventFeature

# 节前调休：使用线性衰减（距离假期越近，影响越大）
event_pre = EventFeature(
    event_name="spring_festival_pre",
    event_start_dates=spring_festival_df["pre_start"],
    event_end_dates=spring_festival_df["pre_end"],
    window=None,
    saturation="linear"  # 线性衰减（可选"logistic"或"exponential"）
)

# 生成特征矩阵
pre_matrix = event_pre.get_event_features(df["date"])
df["spring_festival_pre_saturated"] = pre_matrix["spring_festival_pre"]

更新模型

model = LGT(
    response_col="orders",
    date_col="date",
    regressor_col=[
        "spring_festival_pre_saturated",  # 带衰减的节前特征
        "event_spring_festival_holiday",
        "event_spring_festival_post"
    ],
    # 其他参数不变...
)

查看节假日系数

# 获取回归系数后验分布
coef_samples = model.get_regression_coefs()

# 绘制系数分布
import matplotlib.pyplot as plt
plt.figure(figsize=(12, 4))
plt.subplot(131)
plt.hist(coef_samples["event_spring_festival_pre"], bins=30)
plt.title("节前调休系数")
plt.subplot(132)
plt.hist(coef_samples["event_spring_festival_holiday"], bins=30)
plt.title("正式假期系数")
plt.subplot(133)
plt.hist(coef_samples["event_spring_festival_post"], bins=30)
plt.title("节后调休系数")
plt.show()

可视化节假日影响

# 预测结果分解
predicted = model.predict(df)
model.plot_components(
    predicted,
    plots=["regressors"],
    figsize=(10, 4),
    title="春节各阶段影响"
)

高级配置参数

不同节假日独立配置

为不同节假日设置不同的窗口和阶数：

# 定义多个节假日
holidays_df = pd.DataFrame({
    "date": ["2023-01-01", "2023-12-25"],
    "holiday_name": ["NewYear", "Christmas"],
    "window": [3, 2]  # NewYear影响3天，Christmas影响2天
})

# 生成特征时按不同窗口处理
df = get_event_prediction(
    df=df,
    date_col="date",
    event_df=holidays_df,
    event_name_col="holiday_name",
    event_window_col="window"  # 指定窗口列
)

节假日效应阶数（Saturation）

控制节假日影响的非线性程度（如逐渐衰减）：

from orbit.features import EventFeature

# 自定义节假日特征（使用逻辑函数衰减）
event = EventFeature(
    event_name="SpringFestival",
    event_date="2023-01-02",
    window=3,
    saturation="logistic"  # 衰减模式
)

# 生成特征矩阵
event_matrix = event.get_event_features(df["date"])
df = pd.concat([df, event_matrix], axis=1)

实际应用示例

场景：电商促销日预测

目标：预测包含“双十一”促销节日的销售额。

步骤：

定义促销节假日：

promotions_df = pd.DataFrame({
    "date": ["2023-11-11", "2023-06-18"],
    "holiday_name": ["Double11", "618Sale"]
})

生成促销特征（促销前后3天）：

df = get_event_prediction(
    df=df,
    date_col="date",
    event_df=promotions_df,
    event_name_col="holiday_name",
    event_window=3
)

训练模型：

model = LGT(
    response_col="sales",
    date_col="date",
    regressor_col=["holiday_Double11", "holiday_618Sale"],
    seasonality=365.25,
    estimator="stan-mcmc"
)
model.fit(df)

分析节假日影响：

# 查看节假日系数后验分布
import seaborn as sns
samples = model.get_regression_coefs()  # 获取回归系数样本
sns.histplot(samples["holiday_Double11"], kde=True)

验证与调试

验证节假日是否生效

• 方法1：检查模型预测结果中节假日的突变点是否符合预期。
• 方法2：对比包含和不包含节假日特征的模型指标（如WMAPE）。

调试技巧

• 过拟合检查：若节假日系数置信区间过宽，可能是数据不足或窗口过长。
• 特征重要性：通过 plot_components() 可视化节假日贡献：

predicted = model.predict(df)
model.plot_components(predicted, plots=["regressors"])

注意事项

• 日期格式：确保 date 列已转换为 datetime 类型。
• 预测期覆盖：预测区间内的节假日需提前在 event_df 中定义。
• 多重节假日：若多个节假日重叠，模型会自动叠加效应。
• 国际化节假日：针对不同地区数据，需本地化节假日定义（如中国的春节 vs 美国的圣诞节）。

自动处理季节性

季节性自动检测与建模原理

Orbit 的季节性处理基于结构化时间序列模型（如 LGT、DGLM），通过以下步骤实现自动化：

频率推断

• 输入数据频率：根据 date_col 的间隔自动推断基础频率（如 H 小时、D 天、M 月）。
• 默认季节性周期：
  • 小时级数据：seasonality=24（日周期性）。
  • 天级数据：seasonality=7（周周期性）。
  • 月级数据：seasonality=12（年周期性）。

傅里叶级数展开（可选）

对于需要显式周期分解的场景（如非线性模型 DGLM）：

• 傅里叶基函数：自动生成正弦/余弦项，近似周期性模式。

# 示例：生成周季节性（周期=7，阶数=3）
fourier_terms = orbit.features.fourier_series(df["date"], period=7, order=3)
df = pd.concat([df, fourier_terms], axis=1)

平滑技术

• 局部平滑（LGT 模型）：使用贝叶斯方法动态调整季节性强度，适应模式变化。
• 全局平滑（DGLM 模型）：假设季节性模式固定，通过回归系数学习周期性。

基础配置方法

单季节性配置

from orbit.models import LGT

model = LGT(
response_col="sales",
date_col="date",
seasonality=7, # 周季节性（周期=7 天）
estimator="stan-mcmc"
)
model.fit(df)

多季节性配置

添加 extra_seasonalities 参数支持多个周期：

model = LGT(
response_col="electricity_demand",
date_col="date",
seasonality=24, # 主季节性：日周期（24 小时）
extra_seasonalities=[
{"name":"weekly","period":7,"order":3}, # 周周期（3 阶傅里叶）
{"name":"yearly","period":365.25,"order":5} # 年周期（5 阶傅里叶）
],
estimator="stan-mcmc"
)

高级配置与调优

季节性阶数（order）

控制季节性的灵活度，阶数越高越敏感（但可能过拟合）：

extra_seasonalities=[
{"name":"yearly","period":365.25,"order":5} # 5 阶傅里叶项
]

非整数周期

处理如年周期（365.25 天）或季度周期（91.31 天）：

extra_seasonalities=[
{"name":"quarterly","period":91.31,"order":2}
]

动态平滑强度（LGT 专属）

通过 seasonality_smoothing_strength 调整局部平滑程度：

model = LGT(
seasonality=7,
seasonality_smoothing_strength=0.8, # 值越大，季节性越稳定（0~1）
estimator="stan-mcmc"
)

实际应用示例

零售业周季节性建模

场景：预测商超每周的销售额波动（周末高峰）。

model = LGT(
response_col="sales",
date_col="date",
seasonality=7, # 周季节性
extra_seasonalities=[
{"name":"yearly","period":365.25,"order":4}
],
estimator="stan-mcmc"
)
model.fit(df)

小时级交通流量预测

场景：预测城市每小时的车流量（早晚高峰+日周期）。

model = LGT(
response_col="traffic_volume",
date_col="date",
seasonality=24, # 日周期性（24 小时）
extra_seasonalities=[
{"name":"weekly","period":7*24,"order":2} # 周周期（以小时为单位）
],
estimator="pyro-svi" # 使用变分推断加速计算
)

季节性诊断与可视化

成分分解

predicted = model.predict(df)
model.plot_components(
predicted,
plots=["seasonality"], # 仅显示季节性
figsize=(10,4),
title="周季节性分解"
)

后验分布检查

# 获取季节性系数样本（以周季节性为例）
samples = model.get_seasonality_coefs(seasonality_name="weekly")

# 绘制系数分布
import seaborn as sns
sns.histplot(samples, kde=True)
plt.title("周季节性系数后验分布")

常见问题与解决方案

过拟合表现

• 症状：验证集表现远差于训练集。
• 解决：
  • 降低 order 值（如从 5 阶减至 3 阶）。
  • 增加 seasonality_smoothing_strength（LGT 模型）。

计算开销过大

症状：模型训练时间过长。
• 解决：
  • 使用 estimator=”stan-map”（最大后验估计）替代 MCMC。
  • 减少 extra_seasonalities 的数量或阶数。

忽略重要季节性

• 症状：模型未捕捉到已知周期性（如季度波动）。
• 解决：
  • 显式添加 extra_seasonalities。
  • 检查数据频率是否与周期匹配（如月数据无法建模日季节性）。

外部协变量处理

核心概念

外部协变量（Regressors）指对目标变量有潜在影响的独立变量（如促销活动、天气数据、竞争对手价格等）。Orbit 通过贝叶斯回归模型将协变量整合到预测流程中，支持以下类型：

• 数值型：连续变量（如广告支出金额）。
• 二元型：0/1 标志（如是否促销）。
• 动态/静态：随时间变化或固定（如区域编码）。

数据准备

协变量对齐

• 时间对齐：协变量必须与目标变量 date_col 严格对齐。
• 示例数据结构：

import pandas as pd
df = pd.DataFrame({
"date": ["2023-01-01", "2023-01-02", "2023-01-03"],
"sales": [100, 150, 200], # 目标变量
"ad_spend": [500, 800, 600], # 数值型协变量
"is_promotion": [0, 1, 0], # 二元型协变量
"temperature": [25, 28, 22] # 天气数据
})

缺失值处理

• 前向填充：对时间序列协变量使用 ffill。
• 插值法：连续变量可用线性插值。

df["ad_spend"].interpolate(method="linear", inplace=True)

模型配置

声明协变量

通过 regressor_col 参数指定协变量列：

from orbit.models import LGT

model = LGT(
response_col="sales",
date_col="date",
regressor_col=["ad_spend", "is_promotion", "temperature"],
estimator="stan-mcmc"
)
model.fit(df)

回归系数约束

先验分布：通过 regressor_sigma_prior 约束系数范围。

model = LGT(
regressor_col=["ad_spend", "is_promotion"],
regressor_sigma_prior=[0.5, 0.5], # 标准差先验（高斯分布）
estimator="stan-mcmc"
)

较小的 sigma 值表示对系数幅度的强约束。

动态滞后效应

为协变量添加滞后项（如广告效果的延迟影响）：

# 生成广告支出的滞后特征（滞后 1 天）
df["ad_spend_lag1"] = df["ad_spend"].shift(1)

# 更新模型配置
model = LGT(
regressor_col=["ad_spend", "ad_spend_lag1"]
)

高级功能

非线性效应

使用样条函数或分箱处理非线性关系：

from orbit.features import SplineTransformer

# 创建温度的非线性特征（3 个样条基函数）
spline = SplineTransformer(variable="temperature", n_knots=3)
df = spline.fit_transform(df)

# 更新模型协变量列
model = LGT(
regressor_col=spline.get_feature_names() # 如["spline_temp_1", "spline_temp_2"]
)

交互效应

手动创建交互项（如促销与广告的协同效应）：

df["promo_x_ad"] = df["is_promotion"] * df["ad_spend"]
model = LGT(regressor_col=["promo_x_ad"])

实际应用示例

场景：电商促销预测

目标：预测促销活动、广告支出对销售额的影响。

数据准备：

df = pd.DataFrame({
"date": pd.date_range(start="2023-01-01", periods=30),
"sales": [120, 150, ..., 300], # 目标变量
"ad_spend": [500, 600, ..., 800],
"is_promotion": [0, 0, ..., 1],
"competitor_price": [100, 95, ..., 105]
})

模型配置：

model = LGT(
response_col="sales",
date_col="date",
regressor_col=["ad_spend", "is_promotion", "competitor_price"],
seasonality=7,
regressor_sigma_prior=[0.3, 0.2, 0.5], # 约束广告和竞对系数
estimator="stan-mcmc"
)
model.fit(df)

结果分析：

# 获取协变量后验分布
coef_samples = model.get_regression_coefs()

# 计算广告支出的 ROI（假设广告单位：千元）
roi_samples = coef_samples["ad_spend"] * 1000 # 每千元广告费带来的销售额增长
print(f"广告 ROI 95% 置信区间：{np.quantile(roi_samples, [0.025, 0.975])}")

验证与诊断

协变量重要性

predicted = model.predict(df)
model.plot_components(
predicted,
plots=["regressors"], # 可视化协变量贡献
figsize=(10, 4)
)

敏感性分析

通过扰动协变量值评估影响：

# 创建场景：广告支出增加20%
df_scenario = df.copy()
df_scenario["ad_spend"] = df["ad_spend"] * 1.2

# 预测对比
predicted_scenario = model.predict(df_scenario)
impact = predicted_scenario["prediction"] - predicted["prediction"]
print(f"广告增加20%带来的平均日销售额提升：{impact.mean()}")

注意事项

• 共线性检查：高相关性的协变量需合并或剔除（使用VIF检测）。
• 未来数据可用性：预测期协变量必须已知或可推测。
• 业务解释性：避免使用无法解释的”黑盒”协变量。
• 稀疏性处理：对低频二元变量使用分层模型。

参考链接：

• 官方文档：Orbit Documentation
• GitHub示例：Orbit Examples
• 论文参考：Orbit的LGT/DGLM模型细节见Uber Engineering Blog.