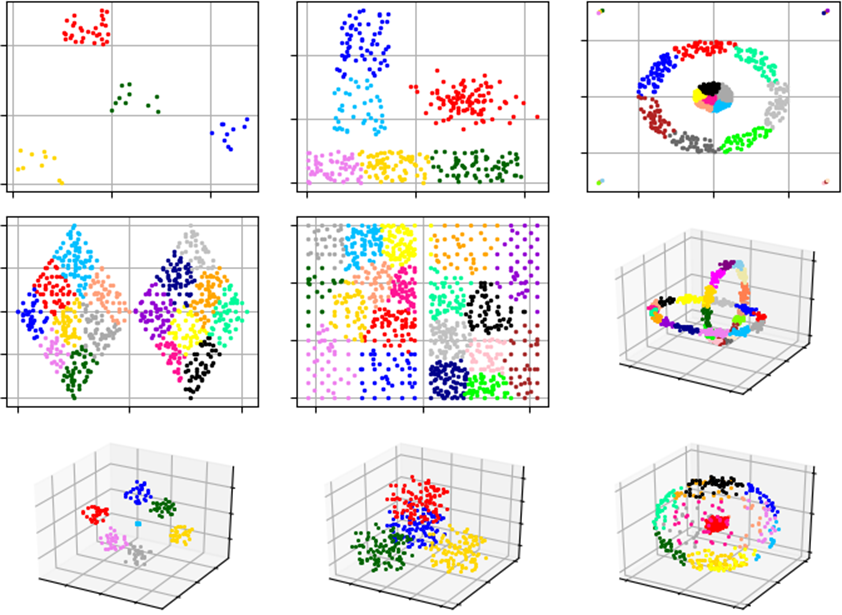
scikit-learn-extra简介
scikit-learn-extra 是 scikit-learn 的一个官方扩展工具包,专为提供那些新颖、专用或尚未纳入主库的机器学习算法而设计。它完全兼容 scikit-learn 的 API 规范,让你能在熟悉的生态里,便捷地使用一些更前沿或更特殊的强大工具。

下面这个表格总结了 scikit-learn-extra 提供的主要功能模块:
| 功能模块 | 核心算法/技术 | 主要特点与应用场景 |
| 聚类分析 | K-Medoids, CLARA, 最近邻聚类 | 提供比K-Means更鲁棒的聚类方案,支持自定义相异度度量,适用于非欧氏空间或存在噪声的数据。 |
| 鲁棒算法 | 稳健回归、分类与聚类 | 通过专门的加权机制削弱异常点对模型训练的影响,提升模型在“脏”数据下的可靠性。 |
| 核方法加速 | 核映射近似 | 通过近似技术大幅提升SVM等核方法的计算效率,使其能处理更大规模的数据。 |
| 高效学习器 | EigenPro | 针对核模型设计的快速训练算法,尤其适用于大规模数据的回归和分类任务。 |
简单来说,scikit-learn-extra 是你在以下情况下的理想选择:
- 当你需要比K-Means更抗干扰的聚类方法时(比如数据有明显异常值,或距离度量非欧氏),可优先考虑K-Medoids。
- 当你的数据污染严重,希望模型能自动识别并忽略异常点时,鲁棒算法模块能提供有力帮助。
- 当你想使用强大的核方法,但苦于计算速度太慢时,核近似技术能为你打开一扇新的大门。
scikit-learn-extra功能详解
scikit-learn-extra 聚类分析模块
scikit-learn-extra 的聚类分析模块提供了一些在标准 scikit-learn 中未包含,但在特定场景下表现优异的聚类算法,特别是 K-Medoids 及其变体,它们在对异常值的鲁棒性、使用任意距离度量等方面具有优势。
下表概括了该模块主要的聚类算法及其核心特点,方便你快速了解:
| 算法名称 | 核心特点 | 最佳适用场景 |
| K-Medoids | 使用实际数据点作为簇中心,对异常值不敏感,支持任意距离度量 | 数据中存在噪声或异常值,需要非欧氏距离度量(如相异度矩阵) |
| CLARA | 通过抽样处理大规模数据集,是 K-Medoids 的高效变种 | 大型数据集的聚类任务,需要在可接受时间内获得近似最优解 |
| Common-nearest-neighbors | 基于局部数据密度和共享近邻概念,能发现复杂形状的簇 | 簇的形状不规则、大小不均,或数据中存在噪声点 |
K-Medoids:更稳健的划分
K-Medoids 是 K-Means 的一种稳健替代方案。
- 工作原理:K-Medoids 选择数据集中实际存在的点(Medoids)作为簇中心,而不是像 K-Means 那样计算簇内点的均值。这个 Medoid 是簇中到其他所有点距离之和最小的点。
- 优势:由于使用真实数据点作为中心,异常值很难对簇中心产生显著影响。K-Medoids 仅通过点对之间的距离进行聚类,不依赖均值计算,因此可用于任何定义了距离度量的数据。
- 代价:K-Medoids 的计算成本通常高于 K-Means,因为它需要频繁计算点对之间的距离。
在 sklearn_extra.cluster中,KMedoids类是其实现。以下是一个简单的代码示例:
from sklearn_extra.cluster import KMedoids
import numpy as np
# 示例数据
X = np.array([[1, 2], [1, 4], [1, 0],
[10, 2], [10, 4], [10, 0]])
# 创建 KMedoids 对象,指定簇数为 2
kmedoids = KMedoids(n_clusters=2, random_state=0)
# 拟合模型并预测标签
labels = kmedoids.fit_predict(X)
# 输出结果
print("簇标签:", labels)
print("Medoids 的索引:", kmedoids.medoid_indices_)
print("Medoids 的坐标:", kmedoids.cluster_centers_)
CLARA:面向大数据的聚类
CLARA 算法通过应用 PAM 方法到多个随机抽取的数据样本上,并返回最佳抽样结果,以适应大型数据集的聚类。
- 工作原理:CLARA 的基本思想是,如果样本具有代表性,那么从样本中找出的最优 Medoids 应该能够较好地代表整个数据集的中心点。其过程是多次随机抽取样本,对每个样本应用 PAM 算法找到一组 Medoids,然后计算这组 Medoids 对整个数据集的聚类质量(如所有点的总代价),最后选择质量最高的那组 Medoids 作为最终结果。
- 优势与局限:CLARA 能够处理 K-Medoids 难以应对的大规模数据集。其聚类质量依赖于样本的代表性,如果样本不能代表整体数据分布,可能无法找到最优聚类。
Common-nearest-neighbors 聚类
Common-nearest-neighbors 聚类,常被称为“共享最近邻聚类”,是一种基于密度和基于图的先进聚类算法。它不依赖于“所有点都在一个球形区域”的假设,因此特别擅长发现任意形状、大小不一的簇,并能有效处理数据中的噪声点。
核心思想
想象一下,在一个人际网络中,判断两个人是否属于同一个“圈子”,不仅要看他们俩是否直接认识,更要看他们有多少个“共同好友”。
Common-nearest-neighbors 算法正是基于这个逻辑:
- 直接邻居:为每个数据点找到其 k 个最近的邻居。
- 共享邻居:计算任意两个点之间共享的最近邻数量。共享邻居越多,说明这两个点所处的局部密度结构越相似,它们属于同一簇的可能性就越大。
- 构建“友情”链接:如果两个点之间的共享邻居数量超过一个设定的阈值,就在它们之间建立一条强连接。
- 寻找“圈子”:最后,所有通过强连接(直接或间接)联系在一起的点,就被归为同一个簇。那些无法与足够多“朋友”建立强连接的点,则被视为噪声。
算法步骤简述
- 构建 k-最近邻图:为数据集中的每个点,找出其 k 个最近的邻居。
- 计算共享最近邻相似度:对于每一对点 i和 j,计算它们共同出现在对方 k-近邻列表中的点的数量。这个数量就是它们相似度的核心度量。
- 定义核心连接:如果点 i和点 j的共享最近邻数量大于等于一个阈值 ,则在它们之间建立一条核心边。这条边比简单的距离度量要稳健得多,因为它基于局部共识。
- 寻找连通分量:将所有通过核心边连接起来的点集视为同一个簇。这通常通过对“核心图”执行连通分量分析来完成。
为何有效?优势与特点
| 特点 | 说明与优势 |
| 识别任意形状簇 | 不假设球形簇,能发现弯曲的、环状的、大小不一的复杂结构。 |
| 对噪声鲁棒 | 噪声点通常与任何簇中的点都没有足够的共享邻居,因此容易被识别并排除。 |
| 自动确定簇数 | 无需预先指定簇的数量,簇的数量由数据的内在结构自然决定。 |
| 对密度变化不敏感 | 相比于传统的 DBSCAN,它通过“共享邻居”的概念,能更好地处理密度差异较大的不同簇。 |
基本使用示例:
import numpy as np
from sklearn.datasets import make_moons
from sklearn_extra.cluster import CommonNNClustering
import matplotlib.pyplot as plt
# 1. 创建具有复杂形状的示例数据(两个半月形)
X, _ = make_moons(n_samples=300, noise=0.05, random_state=0)
# 2. 创建 Common-nearest-neighbors 聚类器
# 关键参数:
# eps_core: 核心边的相似度阈值(共享邻居数)。通常与 `n_neighbors` 相关。
# n_neighbors: 计算邻居时考虑的最近邻数量 `k`。
# min_samples_core: 核心点的最小邻居数,这里我们通过 `eps_core` 控制,此参数通常用默认值。
clusterer = CommonNNClustering(eps_core=5, # 如果两个点有至少5个共享邻居,则连接
n_neighbors=10, # 寻找每个点的10个最近邻
metric='euclidean')
# 3. 执行聚类
labels = clusterer.fit_predict(X)
# 4. 可视化结果
unique_labels = set(labels)
colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]
for k, col in zip(unique_labels, colors):
if k == -1:
# 噪声点标记为黑色
col = [0, 0, 0, 1]
class_member_mask = (labels == k)
xy = X[class_member_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
markeredgecolor='k', markersize=8, label=f'Cluster {k}')
plt.title('Common-nearest-neighbors Clustering')
plt.legend()
plt.show()
关键参数调优建议
- n_neighbors:这是最重要的参数之一。较小的值会使算法对局部结构更敏感,但可能产生更多的小簇和噪声。较大的值会使聚类更平滑,但可能合并一些细节。通常建议从 10 到 30 开始尝试。
- eps_core:共享邻居的阈值。它直接决定了两个点能否被连接。一个经验法则是将其设置为 n_neighbors的 1/3 到 1/2。例如,n_neighbors=15时,eps_core=5是个合理的起点。
- metric:距离度量。对于数值型数据,‘euclidean’(欧氏距离)是默认且常用的选择。对于非数值数据,可以使用自定义距离函数。
总结:何时选择 Common-nearest-neighbors?
- 当数据簇的形状复杂(如流形、环形、交叉),而 K-Means 或 K-Medoids 等算法失效时,这是你的首选。
- 当数据中包含大量噪声,且你希望算法能自动过滤掉它们时。
- 当你不知道数据中有多少个簇,希望算法能自动发现时。
代价:与 K-Means 相比,Common-nearest-neighbors 的计算成本更高,因为它需要计算所有点对之间的 k-最近邻关系,时间复杂度通常在。同时,它对参数也更敏感,需要进行一定的调参。
如何选择聚类算法
- 数据量:数据量巨大时,可优先考虑 CLARA。数据量适中且追求聚类稳健性时,K-Medoids 是个不错的选择。
- 簇的形状:如果怀疑数据中存在复杂形状的簇(如流形、环形),Common-nearest-neighbors 这类基于密度的算法可能比基于划分的算法(如 K-Medoids)表现更好。
- 数据质量:当数据中存在显著异常值时,K-Medoids 通常比 K-Means 更稳健。
scikit-learn-extra鲁棒算法
scikit-learn-extra 提供的鲁棒算法模块专为在数据存在异常值、噪声或模型假设不完全满足的情况下,仍能保持稳定性能的模型而设计。以下是其核心鲁棒算法的详细介绍。
| 算法类别 | 核心机制 | 适用场景 | 关键优势 |
| 鲁棒回归 | 稳健加权(M-估计器) | 数据中存在少量到中等比例的异常响应值(y-异常) | 通过迭代重加权减小异常点影响,无需直接删除数据 |
| 鲁棒分类 | 稳健损失函数与加权 | 标签噪声、训练样本存在错误标注 | 对错误标注的样本赋予低权重,提升决策边界准确性 |
| 鲁棒聚类(如K-Medoids) | 优化目标基于实际数据点(Medoids) | 数据中存在异常值,或距离度量非欧几里得 | 使用数据点作为簇中心,对异常值不敏感,且适用于任意相异度度量 |
鲁棒回归与分类
这类算法的核心思想是采用稳健加权(M-估计器) 的方法。与传统最小二乘法对所有样本误差一视同仁不同,它们通过迭代过程为每个样本分配权重:与模型预测差异巨大的异常点会被赋予较小的权重,从而显著降低其对模型参数估计的负面影响,而不是被完全剔除。这个过程通常是:先用初始模型做预测,然后根据预测残差计算每个样本的权重(异常点权重小),最后用新权重更新模型,并多次迭代直至收敛。
在scikit-learn-extra中,这类算法的实现通常与scikit-learn中的稳健回归器(如RANSACRegressor、TheilSenRegressor和HuberRegressor)有相似的思路,但可能提供了不同的权衡或实现方式 。例如,HuberRegressor就对中度异常值表现稳健,且不影响对干净数据的估计效率 。
鲁棒聚类(K-Medoids)
KMedoids算法是鲁棒聚类的重要代表,也是scikit-learn-extra的亮点。与K-Means使用簇内样本均值作为中心不同,K-Medoids选择簇内一个实际存在的样本点(Medoid)作为中心,该点是簇内到其他所有点距离之和最小的点 。
这种做法带来两大优势:
- 对异常值不敏感:由于中心点是真实数据点,而非计算出的均值,个别极端异常值很难将中心点“拉偏” 。
- 灵活的相异度度量:算法仅依赖于点对之间的距离(或更一般地,相异度)工作,不依赖于均值的计算。因此,你可以使用任意定义的相异度度量,如曼哈顿距离、余弦相异度,甚至是针对特定数据类型(如时间序列)的自定义距离度量,这使得它能应用于非欧氏空间的数据 。
一个简单的代码示例如下:
from sklearn_extra.cluster import KMedoids
import numpy as np
# 示例数据
X = np.array([[1, 2], [1, 4], [1, 0],
[10, 2], [10, 4], [10, 0]])
# 创建KMedoids对象,指定簇数为2,使用'recom'方法进行初始化(更高效)
kmedoids = KMedoids(n_clusters=2, metric='euclidean', method='recom', random_state=0)
# 拟合模型并预测标签
labels = kmedoids.fit_predict(X)
print("簇标签:", labels)
print("Medoids的索引:", kmedoids.medoid_indices_)
print("Medoids的坐标:\n", kmedoids.cluster_centers_)
鲁棒算法应用建议
- 算法选择参考
- 当怀疑数据中存在异常响应值(y-异常) 时,可优先考虑鲁棒回归算法 。
- 对于标签噪声问题,可尝试鲁棒分类方法。
- 当数据中存在异常点,或者你需要使用非欧氏距离(如编辑距离、杰卡德距离等)进行聚类时,KMedoids通常是比K-Means更优的选择 。
- 参数调优与评估
- 鲁棒回归/分类中,关注与加权函数相关的参数(如权重调整的阈值)。
- 对于KMedoids,metric参数至关重要,它决定了距离度量方式。初始化方法(method)也会影响结果和速度,’recom’通常是一个高效的选择 。
- 评估鲁棒聚类结果可能更具挑战性。如果数据有真实标签,可以使用调整兰德指数(Adjusted Rand Index, ARI)或标准化互信息(NMI)等外部指标;若无真实标签,轮廓系数等内部指标可作参考,但需谨慎解读。
- 与主库算法的对比与选择
- scikit-learn主库提供了如RANSAC、Theil-Sen和HuberRegressor等鲁棒回归器 。scikit-learn-extra中的鲁棒回归算法可能提供了不同的实现或特性。
- 在聚类方面,scikit-learn-extra的KMedoids弥补了主库在基于实际点中心的聚类算法方面的空白,与主库的DBSCAN等基于密度的算法形成互补 。DBSCAN能发现任意形状的簇并对噪声有鲁棒性,但它不依赖于中心点的概念,且不需要预先指定簇数 。
简要总结
scikit-learn-extra的鲁棒算法模块为处理“不完美”数据提供了有力工具。当你的数据集中存在异常值、噪声,或者需要更通用的距离度量时,这个模块中的算法(特别是KMedoids)值得尝试。理解其核心的稳健加权思想和基于真实中心点的聚类理念,能帮助你更有效地在项目中选择和应用它们。
希望这些信息能帮助你更好地理解scikit-learn-extra中的鲁棒算法。如果你对某个特定算法的具体使用场景或参数调整有更深入的疑问,我们可以继续探讨。
scikit-learn-extra核方法加速
scikit-learn-extra 通过核映射近似技术,巧妙地解决了传统核方法(如支持向量机、核PCA等)在面对大规模数据时计算成本高昂的问题,让你能在普通计算机上处理原本难以应对的大规模非线性问题。
下表概括了核方法加速的核心机制与价值。
| 特性 | 传统核方法 | scikit-learn-extra 的加速方法 |
| 核心原理 | 隐式使用“核技巧”,依赖计算所有样本对的核矩阵 | 显式构造低维近似特征映射,绕过巨大核矩阵的计算 |
| 计算复杂度 | 时间和空间复杂度通常为 O(n²) 或更高,n为样本数 | 利用Fastfood等技术,复杂度可降至约O(m log d),m为指定分量数,d为特征数 |
| 内存消耗 | 需存储巨大的核矩阵,内存开销大 | 仅存储低维特征映射,内存需求显著降低 |
| 适用场景 | 中小规模数据集 | 大规模数据集的非线性学习任务 |
| 与线性模型结合 | 通常需专用核化算法 | 可与更高效的线性模型(如线性SVM)结合使用 |
核方法为何需要加速
核方法强大的关键在于“核技巧”(Kernel Trick),它通过一个核函数隐式地将数据映射到高维空间,从而解决复杂的非线性问题,而无需计算高维坐标。但此技巧需计算所有样本对的核函数值并存储为核矩阵,导致计算和存储成本随数据量平方级增长,成为处理大规模数据时的瓶颈。
核映射近似如何工作
核映射近似技术采用了一种截然不同的思路:与其隐式地计算高维内积,不如显式地构造一个低维映射来近似原始核函数对应的特征映射。其核心在于,为给定的核函数找到一个显式的低维特征映射函数φ'(x),使得φ'(x)·φ'(y) ≈ k(x, y)。一旦得到这种低维映射,就可将原始数据x转换为新的低维特征向量φ'(x),然后应用高效的线性算法(如线性SVM)。这样将非线性学习转化为线性学习,同时规避了巨大核矩阵的计算。
在 scikit-learn-extra 中,一个关键的实现是 Fastfood 算法,用于高效近似径向基函数(RBF)核的特征映射。
实际应用与代码示例
在 scikit-learn-extra 中,核映射近似功能通常位于 sklearn_extra.kernel_approximation模块。使用流程通常为:
- 导入相应的近似类(如 Fastfood)。
- 使用 fit或 fit_transform方法从数据中学习映射。
- 得到近似特征映射后,将其输入给一个线性模型。
以下是一个概念性示例,展示如何将核近似与线性SVM结合用于分类任务:
# 注意:此为概念性示例,具体类名和导入路径可能随版本变化
from sklearn_extra.kernel_approximation import Fastfood
from sklearn.linear_model import SGDClassifier
from sklearn.pipeline import make_pipeline
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
# 生成示例数据
X, y = make_classification(n_samples=1000, n_features=50, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
# 创建管道:先进行核映射近似,再用线性分类器
approx = Fastfood(n_components=100, sigma=1.0) # n_components控制近似维度,sigma对应RBF核的gamma
linear_svm = SGDClassifier(loss='hinge', max_iter=1000) # 使用线性SVM
model = make_pipeline(approx, linear_svm)
# 训练模型
model.fit(X_train, y_train)
# 评估模型
score = model.score(X_test, y_test)
print(f"模型准确率: {score:.2f}")
关键参数说明:
- n_components:近似特征映射的维度。此值越大,对核的近似通常越好,但计算成本也越高。需要在精度和效率间权衡。
- sigma(或类似参数):对应原始RBF核函数的 gamma参数,控制核函数的宽度。
除了 Fastfood,该模块还可能提供其他近似方法,如基于随机傅里叶特征(Random Kitchen Sinks)的 RBFSampler等。
简要总结
scikit-learn-extra 中的核方法加速功能通过核映射近似技术,将计算复杂度从依赖样本数平方级降至接近线性级,从而让核方法能够应用于大规模数据集。这种方法允许你继续使用熟悉的 scikit-learn 线性模型,是处理大规模数据非线性问题的实用工具。
希望这些信息能帮助你理解和使用 scikit-learn-extra 的核方法加速功能。如果你对特定算法或具体实现有进一步疑问,我们可以继续探讨。
scikit-learn-extra 的高效学习器
scikit-learn-extra 中的高效学习器模块主要指的是 EigenPro 算法,这是一个专门为大规模核方法(特别是核岭回归和核支持向量机)设计的快速优化算法。下面将详细介绍 EigenPro 的核心原理、优势、使用场景及实际应用。
EigenPro 算法详解
核心问题与解决方案
传统核方法(如核岭回归、SVM)在训练时需要计算并存储整个核矩阵,其时间和空间复杂度分别为 O(n²) 和 O(n²),其中 n 是样本数量。这对于大规模数据集(n > 10,000)来说几乎不可行。
EigenPro 通过以下创新解决了这个问题:
- 随机特征扩展:将核函数近似为随机特征的内积
- 自适应步长优化:根据数据的谱特性自动调整学习率
- 梯度下降加速:通过预计算和缓存关键信息加速迭代
技术原理
EigenPro 的核心思想是对核矩阵的谱特性进行分析,并据此设计出最优的梯度下降步长:
| 优化方向 | 传统随机梯度下降 (SGD) | EigenPro 优化 |
| 步长选择 | 固定或手动调整的学习率 | 基于核矩阵特征值自适应调整 |
| 收敛速度 | 较慢,需多次迭代 | 显著加速,尤其对核矩阵条件数大的情况 |
| 内存使用 | 需存储整个核矩阵或近似 | 只需存储随机特征和预计算的谱信息 |
数学原理:EigenPro 通过分析核矩阵的特征值分布,为不同特征方向分配不同的学习率。对于较大的特征值(对应数据的主要变化方向),使用较小的学习率以确保稳定性;对于较小的特征值(对应数据的细节变化方向),使用较大的学习率以加速收敛。
EigenPro 的优势与特点
| 优势 | 具体说明 |
| 大规模数据处理 | 可处理数十万甚至上百万样本的核方法训练 |
| 自适应优化 | 无需手动调整学习率,算法自动适应数据特性 |
| 内存高效 | 避免了存储整个核矩阵,内存复杂度为 O(nd),其中d是随机特征维度 |
| 收敛保证 | 具有理论收敛保证,尤其对于条件数大的核矩阵 |
EigenPro 实际应用
分类任务示例
from sklearn_extra.kernel_methods import EigenProClassifier, EigenProRegressor
from sklearn.datasets import make_classification, make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, mean_squared_error
# 创建大规模分类数据集
X, y = make_classification(
n_samples=10000, # 1万样本
n_features=20,
n_informative=15,
n_classes=3,
random_state=42
)
# 划分训练测试集
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# 创建 EigenPro 分类器
eigenpro_clf = EigenProClassifier(
n_components=1000, # 随机特征维度
gamma=0.1, # RBF核的gamma参数
n_epochs=5, # 训练轮数
batch_size=100, # 批量大小
random_state=42
)
# 训练模型
eigenpro_clf.fit(X_train, y_train)
# 预测
y_pred = eigenpro_clf.predict(X_test)
# 评估
accuracy = accuracy_score(y_test, y_pred)
print(f"EigenPro分类准确率: {accuracy:.4f}")
# 与传统SVM比较
from sklearn.svm import SVC
svm_clf = SVC(kernel='rbf', gamma=0.1, random_state=42)
svm_clf.fit(X_train, y_train) # 注意:这里可能会很慢!
svm_accuracy = svm_clf.score(X_test, y_test)
print(f"传统SVM分类准确率: {svm_accuracy:.4f}")
回归任务示例
from sklearn_extra.kernel_methods import EigenProClassifier, EigenProRegressor
from sklearn.datasets import make_classification, make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, mean_squared_error
# 创建大规模回归数据集
X, y = make_regression(
n_samples=20000, # 2万样本
n_features=30,
noise=0.1,
random_state=42
)
# 划分训练测试集
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# 创建 EigenPro 回归器
eigenpro_reg = EigenProRegressor(
n_components=2000, # 随机特征维度
gamma=0.05, # RBF核的gamma参数
alpha=0.1, # 正则化参数
n_epochs=10, # 训练轮数
batch_size=200, # 批量大小
random_state=42
)
# 训练模型
eigenpro_reg.fit(X_train, y_train)
# 预测
y_pred = eigenpro_reg.predict(X_test)
# 评估
mse = mean_squared_error(y_test, y_pred)
print(f"EigenPro回归MSE: {mse:.4f}")
print(f"R²分数: {eigenpro_reg.score(X_test, y_test):.4f}")
关键参数详解
| 参数 | 类型 | 说明 | 建议值 |
| n_components | int | 随机特征映射的维度 | 100-5000,取决于数据规模和复杂度 |
| gamma | float | RBF核的带宽参数 | 通过交叉验证调整,通常为 1/(n_features * X.var()) |
| alpha | float | 正则化参数(L2惩罚) | 0.001-1.0,防止过拟合 |
| n_epochs | int | 训练轮数 | 1-20,数据量大时可以减少轮数 |
| batch_size | int | 小批量大小 | 32-1024,受限于内存大小 |
| learning_rate | str/float | 学习率策略 | ‘adaptive’(默认)或具体数值 |
EigenPro 与其他核方法比较
| 方法 | 训练速度 | 内存使用 | 可扩展性 | 适用场景 |
| 传统核SVM | 慢 | 高 | 差 | 小规模数据(n < 10,000) |
| 随机傅里叶特征 | 中 | 中 | 中 | 中等规模数据 |
| Nyström方法 | 中 | 中 | 中 | 中等规模数据 |
| EigenPro | 快 | 低 | 优 | 大规模数据(n > 10,000) |
EigenPro 性能优化建议
超参数调优策略
from sklearn.model_selection import RandomizedSearchCV
import numpy as np
# 定义参数空间
param_dist = {
'n_components': [500, 1000, 2000],
'gamma': np.logspace(-3, 1, 5),
'alpha': np.logspace(-3, 0, 4),
'batch_size': [100, 200, 500]
}
# 随机搜索
search = RandomizedSearchCV(
EigenProClassifier(),
param_dist,
n_iter=20,
cv=3,
scoring='accuracy',
random_state=42,
n_jobs=-1
)
search.fit(X_train, y_train)
print(f"最佳参数: {search.best_params_}")
print(f"最佳分数: {search.best_score_:.4f}")
内存与计算优化
# 使用增量训练处理超大规模数据
from sklearn_extra.kernel_methods import EigenProClassifier
# 创建模型
model = EigenProClassifier(
n_components=1000,
batch_size=1000,
n_epochs=1
)
# 分批加载和训练
batch_size = 10000
for i in range(0, len(X_train), batch_size):
X_batch = X_train[i:i+batch_size]
y_batch = y_train[i:i+batch_size]
model.partial_fit(X_batch, y_batch, classes=np.unique(y))
EigenPro 适用场景总结
- 大规模非线性问题:当数据规模超过传统核方法的处理能力时
- 高维数据:特征维度较高,但样本间存在复杂非线性关系
- 需要快速原型:需要快速验证核方法在数据上的有效性
- 计算资源有限:内存或计算资源不足以运行传统核方法
注意事项与限制
- 参数敏感:n_components和 gamma对性能影响显著,需要调优
- 仅支持RBF核:当前版本主要针对RBF核优化
- 数据标准化:对输入数据的尺度敏感,建议先进行标准化
- 类别平衡:分类任务中,严重不平衡的数据可能影响性能
性能基准测试示例
import time
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn_extra.kernel_methods import EigenProClassifier
from sklearn.svm import SVC
from sklearn.kernel_approximation import RBFSampler
from sklearn.linear_model import SGDClassifier
# 生成不同规模的数据
dataset_sizes = [1000, 5000, 10000, 20000]
results = []
for n_samples in dataset_sizes:
X, y = make_classification(
n_samples=n_samples,
n_features=20,
random_state=42
)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# 标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# EigenPro
start = time.time()
eigenpro = EigenProClassifier(n_components=1000, batch_size=100)
eigenpro.fit(X_train, y_train)
eigenpro_time = time.time() - start
eigenpro_acc = eigenpro.score(X_test, y_test)
# 随机特征+SGD(对比方法)
start = time.time()
rbf_feature = RBFSampler(gamma=0.1, n_components=1000, random_state=42)
X_features = rbf_feature.fit_transform(X_train)
sgd = SGDClassifier(max_iter=1000, tol=1e-3)
sgd.fit(X_features, y_train)
rbf_sgd_time = time.time() - start
rbf_sgd_acc = sgd.score(rbf_feature.transform(X_test), y_test)
results.append({
'n_samples': n_samples,
'EigenPro_time': eigenpro_time,
'EigenPro_acc': eigenpro_acc,
'RBF_SGD_time': rbf_sgd_time,
'RBF_SGD_acc': rbf_sgd_acc
})
# 打印结果
for r in results:
print(f"样本数: {r['n_samples']}")
print(f" EigenPro - 时间: {r['EigenPro_time']:.2f}s, 准确率: {r['EigenPro_acc']:.4f}")
print(f" RBF+SGD - 时间: {r['RBF_SGD_time']:.2f}s, 准确率: {r['RBF_SGD_acc']:.4f}")
print()
EigenPro 是 scikit-learn-extra 中处理大规模核学习问题的高效解决方案,特别适合需要核方法强大表达能力但面临计算资源限制的场景。通过合理的参数调优,它可以在保持高精度的同时,显著提升训练速度。
参考链接: