理论基础与核心逻辑
布鲁姆认知金字塔
布鲁姆认知金字塔(Bloom’s Cognitive Taxonomy)是由美国教育心理学家本杰明·布鲁姆(Benjamin Bloom)及其团队于1956年提出的教育目标分类框架,旨在帮助教育者设计和评估教学活动的认知复杂度。这一分类法将学习目标分为由低到高的六个层次,强调从基础记忆到高阶批判性思维和创造力的逐步提升。2001年,该分类法经过修订,进一步优化了术语和结构,使其更符合现代教育需求。
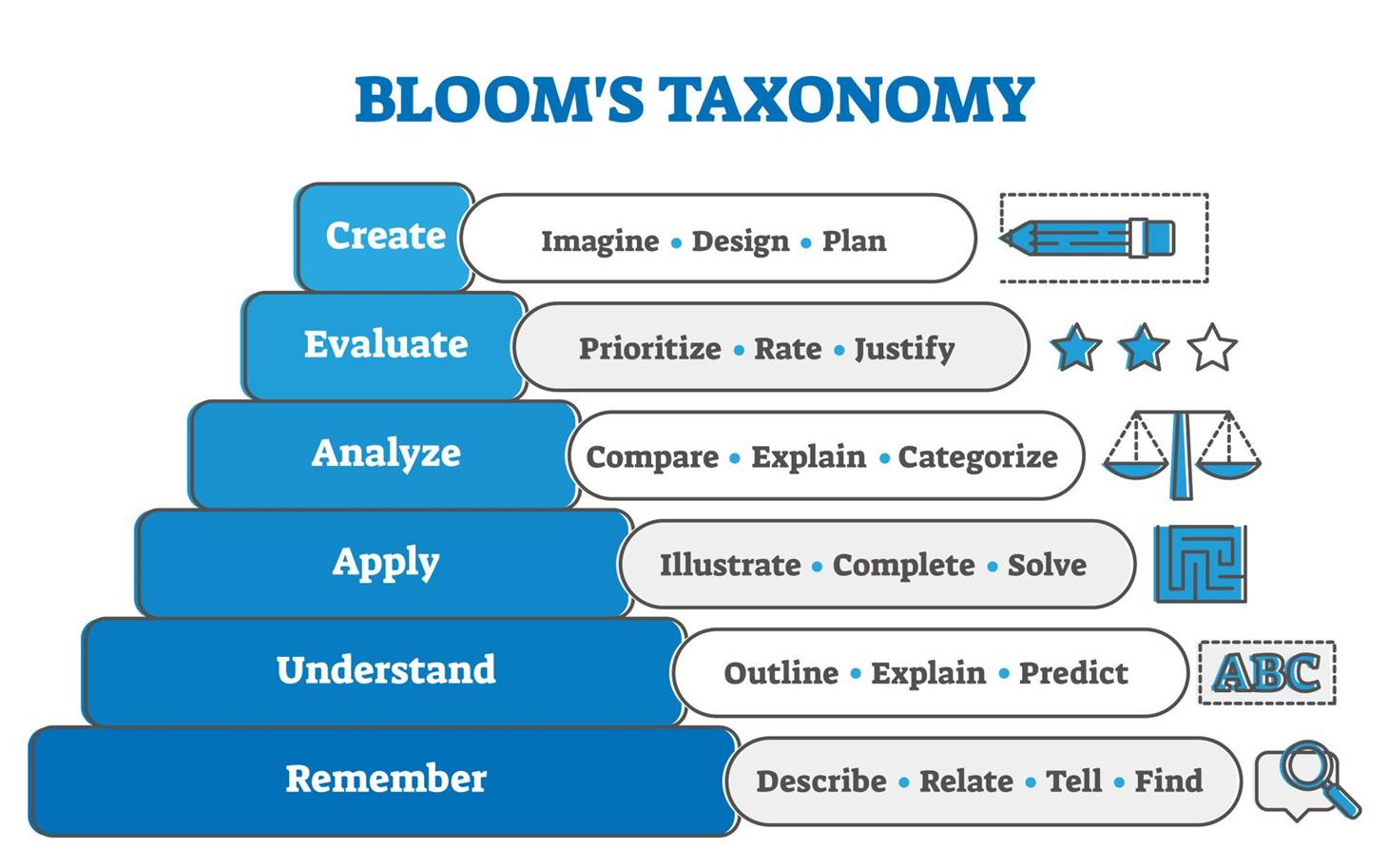
以下是布鲁姆认知金字塔的详细分层(以修订版为主,结合经典版对比):
记忆(Remember)
- 定义:识别或回忆基本信息(事实、概念、术语等)。
- 目标动词:列举、复述、定义、记忆、识别。
- 示例:
- 背诵化学元素周期表;
- 写出历史事件的时间线;
- 识别数学公式中的符号含义。
- 教学应用:通过填空题、选择题、背诵任务等检验基础知识。
理解(Understand)
- 定义:用自己的语言解释信息的意义,包括转述、分类或总结。
- 目标动词:解释、比较、举例、归纳、总结。
- 示例:
- 用图表说明光合作用的过程;
- 比较不同文学体裁的特点;
- 用简单语言总结一篇论文的核心观点。
- 教学应用:通过讨论、思维导图、摘要写作等活动培养理解力。
应用(Apply)
- 定义:将所学知识运用于新情境或解决实际问题。
- 目标动词:使用、计算、执行、解决、模拟。
- 示例:
- 用勾股定理测量现实中的距离;
- 编写程序代码实现特定功能;
- 设计实验验证物理定律。
- 教学应用:通过案例分析、实验操作、项目实践等方式强化知识迁移能力。
分析(Analyze)
- 定义:将复杂信息分解为部分,探究其内在关系和结构。
- 目标动词:区分、解构、关联、推断、组织。
- 示例:
- 分析小说中的人物动机;
- 拆解一台机器的运作原理;
- 辨别新闻报道中的偏见。
- 教学应用:通过辩论、批判性阅读、数据图表分析等培养逻辑思维。
评价(Evaluate)
- 定义:基于标准或证据对信息、方法或观点进行判断。
- 目标动词:批判、辩护、评估、判断、验证。
- 示例:
- 评价某环保政策的有效性;
- 比较不同算法的效率并选择最优方案;
- 审阅一篇科研论文的论证逻辑。
- 教学应用:通过论文评审、辩论赛、同行互评等活动培养判断力。
创造(Create)
- 定义(修订版新增):将元素重组或整合,生成新的观点、方案或作品。
- 目标动词:设计、发明、创作、整合、构建。
- 示例:
- 编写原创剧本;
- 开发一款解决实际问题的APP;
- 提出一种新的理论模型。
- 教学应用:通过开放性项目、艺术创作、创业计划等激发创新能力。
经典版 vs 修订版对比
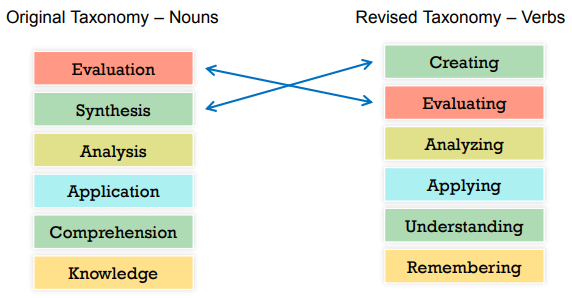
- 经典版(1956):知识、理解、应用、分析、综合、评价。
- 修订版(2001):将“综合”改为“创造”,并调整层次顺序为:记忆、理解、应用、分析、评价、创造。
- 关键变化:从名词到动词的转变(强调学习者的行动),以及更突出“创造”作为最高阶目标。
教育意义
- 课程设计:帮助教师设计从简单到复杂的教学目标。
- 问题设计:指导课堂提问和考试命题的深度(例如低阶选择题 vs 高阶开放式问题)。
- 评估反馈:通过分层目标衡量学生认知水平。
- 技术结合:数字工具(如思维导图软件、编程平台)可辅助实现高阶目标。
争议与批评
- 灵活性:并非所有学习都需严格遵循线性层级,部分情境可能需要跳跃或混合层次。
- 文化差异:某些文化可能更重视记忆而非创造力,导致金字塔适用性受限。
- 情感与技能:布鲁姆分类法未涵盖情感(态度)和动作技能领域,需结合其他模型(如 Krathwohl 的情感分类法)。
布鲁姆认知金字塔至今仍是教育领域的基础工具,其核心理念——“学习是思维逐级深化的过程”——为教学设计和评估提供了清晰的框架
- 在理解一个概念之前,你需要记住它;
- 要应用一个概念,你首先需要理解它;
- 要评估一个过程,你首先需要分析它;
- 要创造新的东西,你需要完成彻底的评估。
知识晶体化理论
知识晶体化理论(Knowledge Crystallization Theory)是一种描述知识从碎片化、无序状态逐渐转化为结构化、系统化认知框架的过程模型。它强调知识在学习和应用中的整合与内化,通常与认知科学、教育心理学和知识管理领域相关。
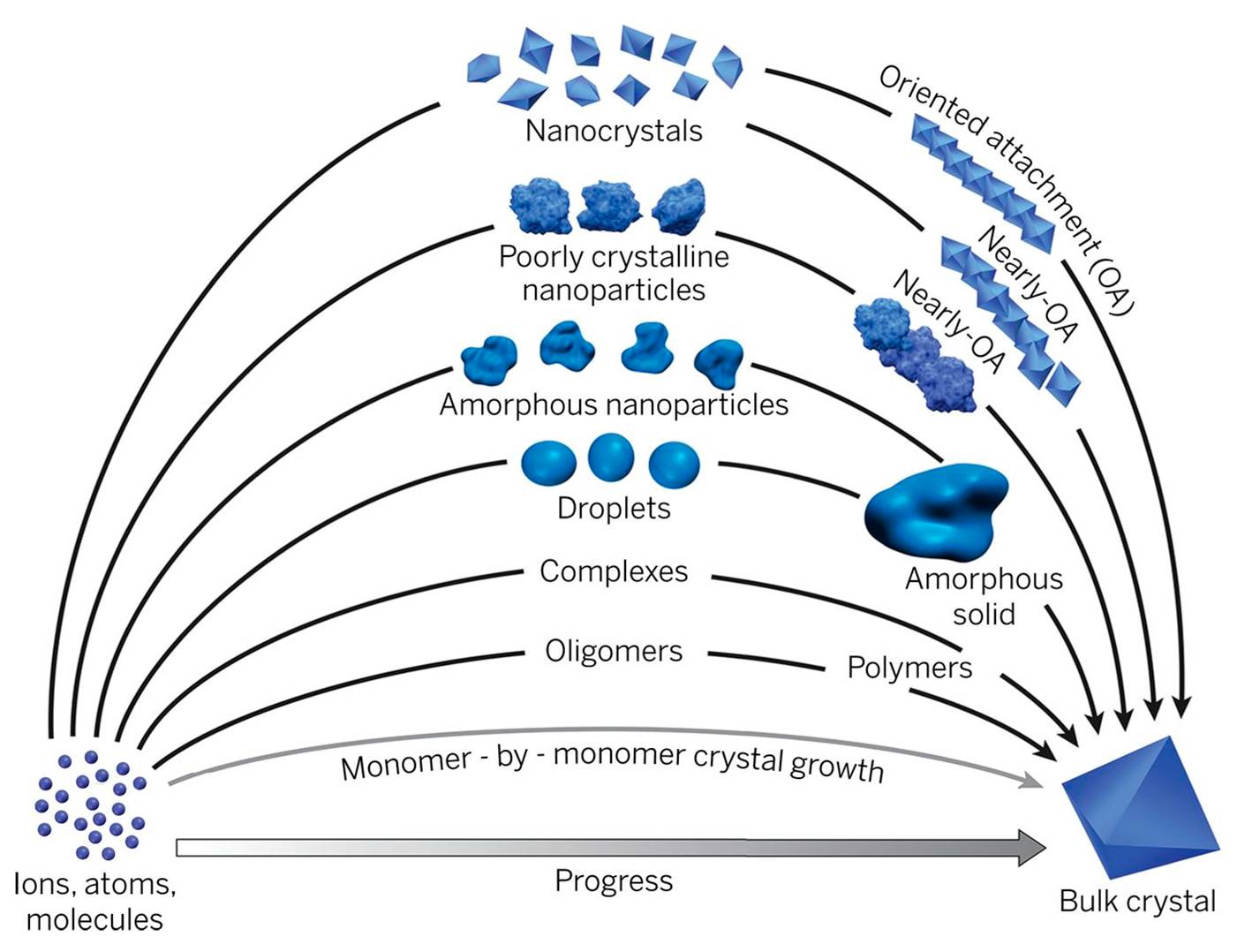
知识晶体化指个体通过持续学习、实践和反思,将零散的信息(如事实、概念、经验)逐步组织成相互关联、逻辑清晰的认知结构(即“知识晶体”),从而提升知识的存储效率、检索能力和实际应用价值。
理论核心观点
知识形态的演变过程
- 碎片化阶段:初始接触新知识时,信息是孤立的、表面的,例如记住一个公式但不知其应用场景。
- 关联化阶段:通过理解知识间的逻辑关系(如因果关系、类比关系),建立初步连接,例如将公式与物理现象关联。
- 结构化阶段:形成层级分明的知识框架(如学科知识体系),例如理解力学中的“牛顿三定律”如何支撑整个经典力学。
- 晶体化阶段:知识高度整合,可灵活迁移至复杂问题解决,例如用跨学科知识设计环保方案。
晶体化的关键机制
- 重复与强化:通过练习巩固记忆,形成长期记忆痕迹。
- 意义建构:将新知识与已有经验结合,赋予其个人化的理解(建构主义)。
- 模式识别:发现知识中的规律或通用原则(如数学中的“对称性”思想)。
- 情境迁移:在不同场景中应用知识,验证其适用性并调整框架。
阻碍晶体化的因素
- 认知负荷过载:信息量过大导致无法有效整合。
- 缺乏深度思考:仅停留在记忆层面,未建立深层关联。
- 孤立学习:未与其他知识或实践结合,形成“信息孤岛”。
教育与实践中的应用
教学设计策略
- 概念地图(Concept Mapping):用可视化工具(如 Mind Map)展示知识间的层级与关联,帮助学生构建结构化认知。
- 案例式学习(Case-Based Learning):通过真实问题驱动知识整合,例如用商业案例串联经济学、管理学知识。
- 反思性实践(Reflective Practice):引导学生定期总结学习过程,例如撰写学习日志或进行小组复盘。
知识管理中的应用
- 组织知识库建设:将企业内部的隐性经验(如员工技能)转化为显性文档,形成可复用的“知识晶体”。
- 专家系统开发:通过规则引擎和算法模拟人类专家的结构化决策流程。
个人学习优化
- 费曼技巧(Feynman Technique):通过“以教促学”暴露知识漏洞,强化晶体化。
- 间隔重复(Spaced Repetition):利用 Anki 等工具科学复习,减少遗忘曲线的影响。
- 跨学科联想:将不同领域的知识类比联结(如生物学中的“生态系统”类比企业管理)。
相关理论与对比
- 布鲁姆认知目标分类:知识晶体化侧重知识的结构化过程,而布鲁姆分类强调思维层级的递进,两者结合可设计从记忆到创造的教学路径。
- 建构主义学习理论:均强调学习者主动建构意义,但知识晶体化更关注结果的系统性和可迁移性。
- SECI 模型(野中郁次郎):知识晶体化与 SECI 中的“组合化”(显性知识系统化)阶段高度相关。
争议与局限性
- 过度结构化风险:过于追求“晶体化”可能抑制创造性思维,导致知识僵化。
- 个体差异影响:不同学习者的认知风格(如整体型 vs 分析型)可能导致晶体化效率差异。
- 动态知识挑战:在快速变化的领域(如人工智能),旧有知识晶体可能阻碍对新范式的接受。
典型案例
- 医学教育:医学生通过解剖学、病理学、临床实践的多层次整合,最终形成“疾病诊断”的晶体化知识框架。
- 编程学习:从学习语法(碎片)→理解设计模式(关联)→构建软件架构(结构)→开发复杂系统(晶体化)。
未来研究方向
- 神经科学视角:探索知识晶体化与大脑神经网络可塑性的关联(如海马体与皮层的信息整合)。
- AI 辅助晶体化:利用知识图谱和自适应学习系统(如 Knewton)个性化加速知识整合。
- 跨文化差异:比较不同教育体系下知识晶体化的路径差异(如东方强调记忆 vs 西方强调批判性思维)。
知识晶体化理论揭示了知识从无序到有序的动态过程,其核心价值在于为教育者、学习者和组织提供了一套优化认知效率的框架。尽管存在争议,但它仍是理解深度学习和知识创新的重要视角。未来的发展需平衡结构化与灵活性,以适应快速变化的信息时代。
三维知识单元
三维知识单元(Three-Dimensional Knowledge Unit)是一种用于描述和设计知识结构的理论模型,强调从多个维度对知识进行系统性整合,以促进深度学习和跨领域应用。这一概念可能源自教育心理学、知识管理或课程设计领域,尽管它并非广泛公认的标准术语,但可以通过现有理论(如布鲁姆分类法、知识晶体化理论)进行合理推断与构建。
三维整合:以导数知识单元为例
| 维度 | 内容 | 认知目标 | 教学工具 |
| 核心概念 | 导数定义、几何意义、求导规则 | 记忆→理解→应用 | 动画演示、计算练习 |
| 关联路径 | 导数与积分、微分方程、优化的联系 | 分析→评价→创造 | 概念地图、对比案例分析 |
| 应用场景 | 物理速度、经济边际分析、工程优化 | 应用→创造 | 真实项目任务、跨学科合作 |
核心概念(内容属性+认知层次)
维度定位:
- 知识类型:陈述性知识(定义、规则)+程序性知识(计算步骤)。
- 认知层次:理解(解释导数含义)→应用(执行求导运算)。
- 应用情境:学科内情境(纯数学抽象)。
具体内容:
- 导数定义:导数描述函数在某一点处的瞬时变化率,数学表达式为:$f'(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}{h}$
- 认知目标:
- 记忆:复述导数定义公式。
- 理解:用几何意义(切线斜率)或物理意义(瞬时速度)解释导数。
- 应用:对多项式函数(如$f(x)=x^2 $)进行求导计算。
教学示例:
- 通过动画展示割线逼近切线的过程,帮助学生从几何视角理解导数定义。
- 练习求导规则(如幂法则、乘积法则),强化程序性知识。
关联路径(知识网络+认知深化)
维度定位:
- 知识类型:条件性知识(导数与其他概念的关系)+元认知知识(学习策略)。
- 认知层次:分析(比较异同)→评价(判断方法适用性)。
- 应用情境:跨学科情境(数学内部分支的联结)。
核心关联:
- 导数积分:
- 导数与积分是微积分基本定理的两大支柱,互为逆运算。
- 认知目标:
- 分析:通过积分还原原函数,理解两者互逆性。
- 评价:在物理问题中判断何时使用导数(求速度)或积分(求位移)。
- 导数微分方程:
- 导数构成微分方程的核心,用于建模动态系统(如人口增长、热传导)。
- 认知目标:
- 创造:用导数构建简单微分方程模型(如$\frac{dy}{dt}=ky$ )。
- 导数其他数学工具:
- 与泰勒展开(用多项式逼近函数)、优化理论(求极值)的联系。
教学示例:
- 绘制概念地图,连接导数与积分、微分方程、优化问题,形成知识网络。
- 设计对比练习:同一物理问题(如自由落体)分别用导数和积分求解,深化关联理解。
应用场景(实践迁移+高阶思维)
维度定位:
- 知识类型:程序性知识(建模方法)+条件性知识(场景适配)。
- 应用情境:真实世界情境(物理、工程、经济学)。
认知层次:应用(执行计算)→创造(设计解决方案)。
典型场景:
- 物理学:求瞬时速度与加速度
- 若位移函数为$s(t)=5t^2+3t$ ,则:
- 瞬时速度:$v(t)=s'(t)=10t+3$
- 加速度:$a(t)=v'(t)=10$
- 认知目标:
- 应用:从位移函数推导速度与加速度。
- 评价:讨论匀速与加速运动的导数差异。
- 经济学:边际成本与收益分析
- 总成本函数$C(x)$ 的导数$ C'(x) $表示生产第 x 件产品的边际成本。
- 认知目标:
- 分析:比较边际成本与平均成本的关系。
- 创造:提出优化生产规模的策略。
- 工程学:曲线最优化设计
- 用导数求函数极值,设计桥梁拱形曲线或机械零件形状。
- 认知目标:
- 创造:结合材料强度约束,设计最小重量的结构。
- 若位移函数为$s(t)=5t^2+3t$ ,则:
教学示例:
真实项目任务:
- 任务1:用导数分析股票价格变化率,撰写投资建议报告(经济学)。
- 任务2:设计过山车轨道曲线,确保加速度不超过人体承受极限(工程学)。
教育价值
- 避免知识割裂:通过三维模型,学生不仅掌握公式计算,还能理解导数在学科内外的意义。
- 培养高阶思维:从记忆规则到解决复杂真实问题,实现布鲁姆目标的完整覆盖。
- 增强学习动机:真实场景的应用使学生感知数学的实用性,激发探索兴趣。
三维知识单元模型通过核心概念打基础、关联路径建网络、应用场景促迁移,将抽象的数学知识转化为可灵活调用的”认知工具包”。这种结构化、场景化的学习方式,正是应对未来跨学科复杂挑战的关键能力培养路径。
金字塔构建四步法
基础层搭建(20%时间)
操作要点:
- 通过目录扫描定位学科主干(如Python的变量→函数→类→模块)
- 用思维导图建立三级知识框架
- 标注关键术语(加粗红色标记)
示例:(以下知识框架通过Deepseek生成)
#Python基础层框架 -变量系统 ▪基本数据类型(整型/浮点型/字符串/布尔型/None) ▪动态类型与弱类型特性 ▪变量作用域(全局/局部) -流程控制 ▪条件分支(if/elif/else) ▪循环结构(for/while/break/continue) ▪三元表达式 -函数体系 ▪函数定义与调用(def/return) ▪参数传递(位置参数/关键字参数/默认参数) ▪Lambda匿名函数 ▪闭包与装饰器基础 -数据结构 ▪序列类型(列表/元组/范围) ▪映射类型(字典) ▪集合类型(集合/冻结集合) ▪推导式(列表/字典/集合推导式) -异常处理 ▪try/except/finally结构 ▪内置异常类型(ValueError/TypeError等) ▪raise主动抛出异常 ▪自定义异常类 -文件操作 ▪文件读写模式(r/w/a/rb/wb) ▪with上下文管理器 ▪文件路径处理(os.path模块) -模块系统 ▪模块导入机制(import/from) ▪标准库示例(math/datetime/random等) ▪pip包管理工具 ▪虚拟环境(venv) -面向对象编程 ▪类与对象(class/self) ▪构造与析构(__init__/__del__) ▪继承与多态 ▪特殊方法(__str__/__len__等) ▪属性控制(@property/@setter)
连接层编织(30%时间)
关联策略:
- 横向连接:同层级知识关系(如函数与模块的调用关系)
- 纵向连接:跨层级逻辑(变量→函数→类→OOP编程范式)
- 跨学科连接(用数学集合论理解数据库表关系)
视觉化方法:
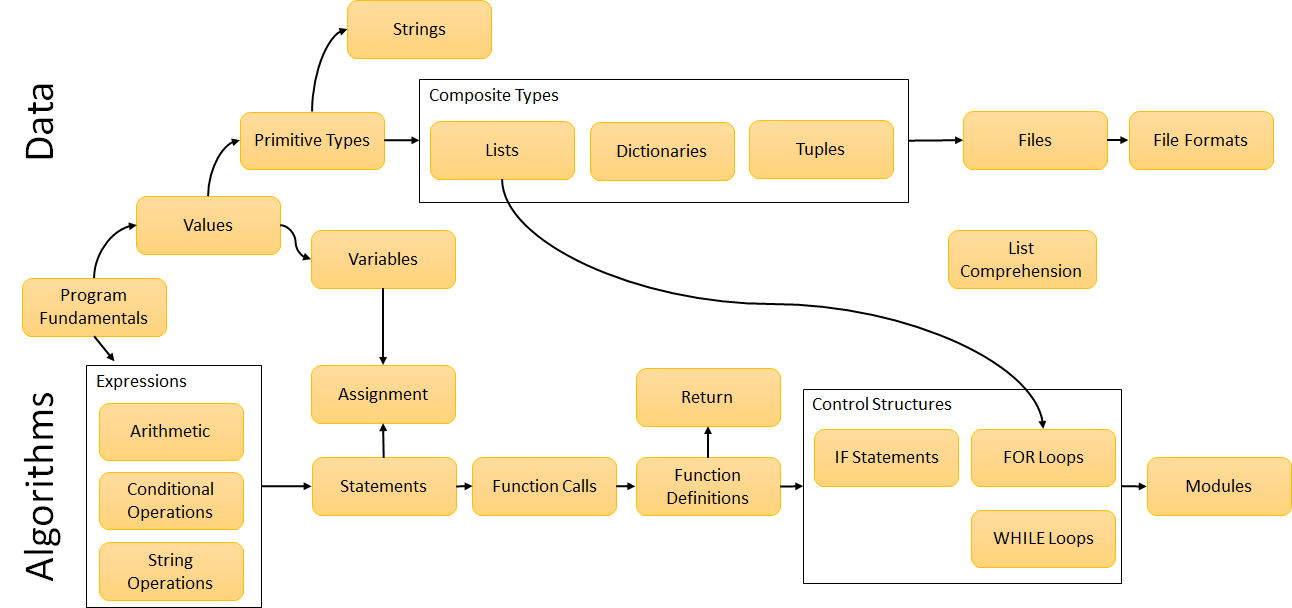
知识连接层示意图详解
绘制五步法
- 确定核心领域
- 工具:用Miro白板划定主题边界
- 示例:以「深度学习」为中心辐射状展开
- 提取知识节点
- 方法:从学习资料中抓取高频术语(≥3次出现的概念)
- 工具:TextRank算法自动提取关键词
- 建立初级连接,规则:
- 教材目录结构→纵向连接
- 跨章节引用→横向连接
- 教师强调的关联→加粗显示
- 添加高阶连接,策略:
- 类比映射:CNN卷积核→生物视觉皮层
- 逆向推导:从论文参考文献找隐藏关联
- 跨学科桥接:用物理熵增原理理解模型过拟合
- 动态优化,迭代机制:
- 每新增10个知识点更新连接路径
- 用Gephi软件分析网络密度,删除孤立节点
应用场景案例
- 案例1:破解学习瓶颈
- 现象:理解RNN结构但不会应用
- 连接层分析:
- 缺失「时间序列分析→RNN」连接
- 缺少「LSTM→梯度消失问题」关联
- 解决方案:补建相关连接并完成股票预测项目
- 案例2:跨学科创新
- 生物学:神经元突触传递
- 计算机:神经网络激活函数
- 连接策略:建立双向类比关系,启发新型激活函数设计
- 案例2:跨学科创新
示意图核心要素
- 节点系统(知识单元)
- 中心节点:核心概念(如机器学习中的「监督学习」)
- 一级节点:直接关联概念(分类/回归/神经网络)
- 二级节点:细分知识点(SVM算法/决策树/LSTM)
- 连接关系(关联路径)
- 实线箭头:强逻辑依赖(如线性代数→机器学习)
- 虚线箭头:弱关联或类比关系(神经网络→人脑结构)
- 颜色编码:
- 🔴红色:因果关系
- 🔵蓝色:包含关系
- 🟢绿色:对立关系
- 层次结构
- 横向层:同领域知识扩展(Python→R→Julia编程语言)
- 纵向层:抽象程度递进(基础语法→设计模式→架构思维)
工具链推荐
| 工具类型 | 推荐工具 | 核心功能 |
| 可视化工具 | Miro/XMind | 手动绘制交互式图谱 |
| 自动化分析 | Gephi/Kumu | 网络密度/中心度分析 |
| 知识管理 | Obsidian/RemNote | 双向链接自动生成示意图 |
| 代码驱动 | Python+NetworkX | 通过代码构建复杂知识网络 |
| 移动端适配 | MindNode/SimpleMind | 随时碎片化更新 |
常见误区与优化
- 连接过度综合症
- 问题:节点间连线超过7条导致认知超载
- 解决:实施「7±2法则」,每个节点保留5-9条关键连接
- 静态固化陷阱
- 问题:完成示意图后不再更新
- 优化:设置每周三下午「连接优化时段」
- 抽象层级混乱
- 错误案例:将「梯度下降」与「深度学习」直接并列
- 修正方法:采用层次化布局插件(如js的力导向图)
效果验证指标
- 连接密度指数
- 计算公式:实际连接数/可能最大连接数
- 健康范围:3-0.6(过高需简化,过低需补充)
- 跨领域桥接率
- 进阶指标:跨学科连接占比≥20%
- 检测方法:标注不同领域颜色后统计比例
- 问题解决响应速度
- 实测方法:随机提出复杂问题,记录定位相关知识点所需时间
应用层拓展(40%时间)
场景化训练:
- 微型项目:每个知识单元对应实操任务(如学完Python函数后编写计算器程序)
- 错题逆向工程:通过错误案例反推知识漏洞
- 跨场景迁移:将编程逻辑应用于Excel公式优化
动态迭代机制(10%时间)
更新策略:
- 每周用绿色标注新增知识点
- 每月用红色删除过时内容(如Python2特有语法)
- 每季度重构框架结构(从基础语法到算法优化)
金字塔构建实践
典型应用场景
新学科入门
案例:机器学习入门
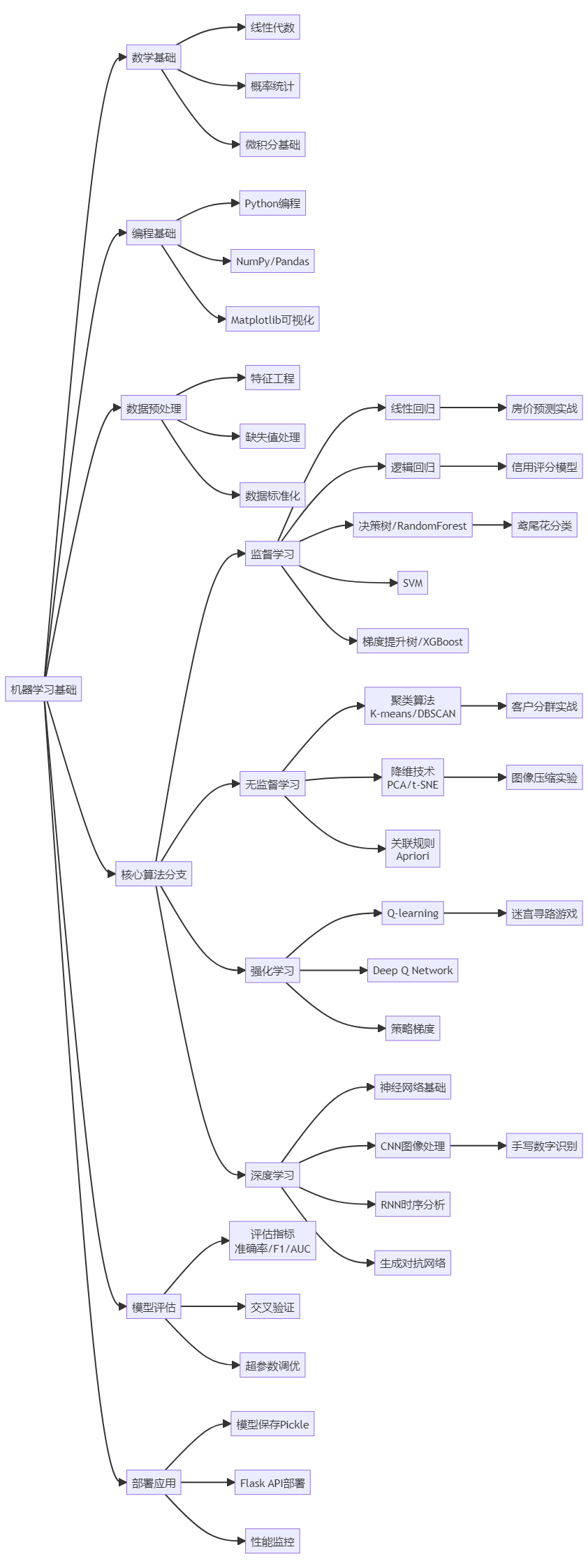
备考复习
四轮复习法:
- 1轮:搭建知识框架(1天)
- 2轮:填充细节内容(3天)
- 3轮:标注高频考点(2天)
- 4轮:模拟问题解决(1天)
技能提升
编程能力升级路径:基础语法→算法思维→系统设计→架构模式→领域建模
工具链支持
| 工具类型 | 推荐工具 | 使用场景 |
| 思维导图 | XMind | 知识框架可视化 |
| 知识库管理 | Notion/Obsidian | 结构化知识存储 |
| 代码实践 | Jupyter Notebook | 即时验证编程知识 |
| 记忆强化 | Anki/Quizlet | 基础概念自动化复习 |
| 版本控制 | GitHub/GitLab | 知识体系迭代记录 |
常见误区与规避
- 知识碎片化陷阱
- 错误表现:收集大量未分类的笔记片段
- 解决方案:强制实施「24小时归档规则」:任何新知识必须在24小时内归类到金字塔对应位置
- 层级跳跃风险
- 错误案例:未掌握SQL基础语法直接学习查询优化
- 规避方法:设置「通关测试」机制,只有基础层掌握度>80%才允许进入下一层级
- 静态化危机
- 错误表现:构建完成后不再更新
- 修正策略:在知识库中添加「时间戳」字段,标注每个节点的最后更新时间
效果验证指标
- 知识提取速度
- 合格标准:能在30秒内定位任意知识点位置
- 测试方法:随机抽题→定位→解决(如:快速找到Python装饰器相关应用案例)
- 问题解决率
- 进阶标准:陌生问题解决率≥65%
- 计算公式:(独立解决的问题数/总尝试问题数)×100%
- 知识迁移能力
- 高阶指标:能生成跨领域解决方案(如用数学建模思路优化工作流程)
实践计划示例
目标:3个月掌握数据分析基础金字塔架构:
- Layer1:Python基础→Pandas操作→SQL语法
- Layer2:数据清洗↔特征工程↔可视化
- Layer3:客户分析报告↔销售预测模型
里程碑:
- 第4周:完成Layer1构建并通过基础测试
- 第8周:用Layer2知识完成Kaggle入门竞赛
- 第12周:产出Layer3级别的商业分析报告
这种结构化建模方法可使学习效率提升3-5倍,建议从一个小型知识领域(如Excel函数库)开始实践,逐步扩展到复杂体系。如果需要特定领域的金字塔构建模板,可以告知具体学习方向。



