GBRank是一种pair-wise的学习排序算法,他是基于回归来解决pair对的先后排序问题。在GBRank中,使用的回归算法是梯度提升数GBT (Gradient Boosting Tree)
算法原理
Learning To Rank需要解决的问题是给定一个Query,如何选择最相关的Document。GBRank核心为将排序问题转化为一组回归问题,对于回归问题可以用GBDT进行求解,也可以用其他的回归函数。
一般来说在搜索引擎里面,相关性越高的越应该排在前面。对于所有的query-document pair,我们从pair抽取出一系列特征对其进行表示。例如query1-document1记为$x$,query1-document2记为$y$。记$x\succ y$表示,用户发起查询query1时,$x$比$y$更适合,更加满足query1的需求。记训练集合为:
$$S=\{{\left\langle{{x_i},{y_i}}\right\rangle|{x_i}\succ{y_i},i=1,…,N}\}$$
给定排序函数空间$H$,我们希望得到一个排序函数$h$ ($h\in H$),当$x_i\succ y_i$时,我们有$h\left({{x_i}}\right)\ge h\left({{y_i}}\right)$。损失函数定义为如下形式:
$$R(h)={1\over 2}{\sum\limits_{i=1}^N{({\max\{{0,h({{y_i}})-h({{x_i}})}\}})}^2$$
这个函数可以解读为,对于训练数据中的一个$\left\langle{{x_i},{y_i}}\right\rangle$,如果$h$学到了这种偏序关系,那么有$h(x_i)>h(y_i)$,$h$对于损失函数的贡献为0,否则为$({h({y_i})-h({x_i})})^2$。直接优化loss比较困难,可以通过改变$h(x_i)$或者$h(y_i)$达到减少loss的目的,例如用回归的方式来拟合$h(x_i)$、$h(y_i)$。
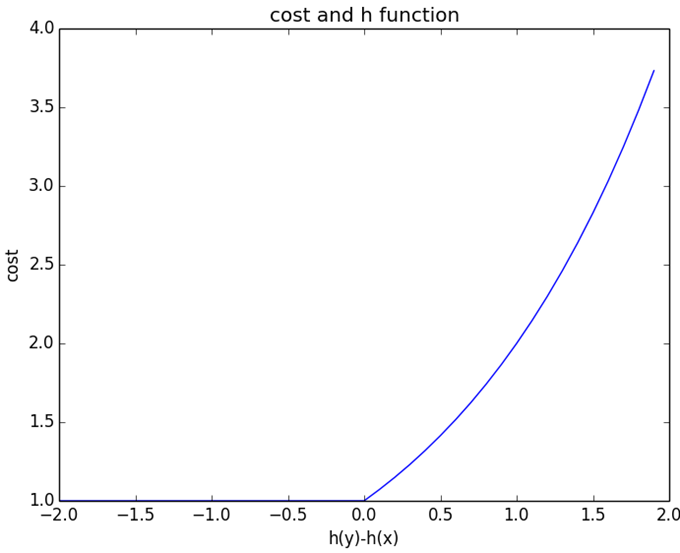
为了避免优化函数$h$是一个常量,在loss fuction上增加一个平滑项$\tau$,$0<\tau\le 1$。在实际应用中$\tau$为固定常数。
$$R(h,\tau)={1\over 2}\sum_{i=1}^{N}(\max\{0,h(y_i)-h(x_i)+\tau\})^2-\lambda\tau^2$$
因为当$h$为常量函数时,原$R(h)=0$就没有再优化的空间了。其实加了平衡项,就变相转为:如果希望$x_i\succ y_i$,就得有$h(x_i)\ge h(y_i)+\tau$,更加严格。多了一个gap。
按一般套路,用梯度下降的方法去最小化loss function。假设有未知函数$h(x_i)$,$h(y_i)$,$i=1,…,N$,loss $R(h)$对$h(x_i)$,$h(y_i)$的负梯度分别为:
$$\max\{0,h(y_i)-h(x_i)\},-\max\{0,h(y_i)-h(x_i)\}$$
当$h$满足$<{x_i},{y_i}>$偏序关系,$h(y_i)-h(x_i)<0$,上面两个梯度都会为0。当$h$不满足$<{x_i},{y_i}>$偏序关系时,梯度为:
$$h(y_i)-h(x_i),h(x_i)-h(y_i)$$
接下来,还需要知道如何将梯度作用到$h$的更新上,通过设定$x_i$的目标值为$h(y_i)+\tau$。$y_i$的目标值为$h(x_i)-\tau$。因此在每轮迭代中,当$h$不满足$<{x_i},{y_i}>$会产生一组数据:
$$\{(x_i,h(y_i)+\tau),(y_i,h(x_i)-\tau)\}$$我们需要拟合本轮产生的所有负例。
GBRank算法:

- 估计一个初始函数$h_0$(任意选择一个都可以)。
- 根据上一轮的$h_{k-1}$,将数据分为两个不相交的子集(正例和负例两个集合):${S^+}=\{\left\langle{{x_i},{y_i}}\right\rangle\in S|{h_{k-1}}({x_i})\ge {h_{k-1}}({y_i})+\tau\}$和$S^-=\{\left\langle x_i,y_i\right\rangle\in S|h_{k-1}(x_i)<h_{k-1}(y_i)+\tau\}$。其中$S^-$作为我们下一步的训练集。
- 使用GBDT拟合负例集合中的数据$\{(x_i,h_{k-1}(y_i)+\tau),(y_i,h_{k-1}(x_i)-\tau)|(x_i,y_i)\in S^-\}$得到$g_k(x)$。(作者设置$\tau=0.1$,其他值也可以尝试。)
- 进行模型的更新:$h_k(x)=\frac{kh_{k-1}(x)+\eta g_k(x)}{k+1}$其中,$\eta$为伸缩因子。
可以看到step3里面每轮都拟合误判的结果,在迭代中这个集合会越来越小。还有一种做法是将曾经误判的集合维持在训练集中,那么训练集就会始终增长。在这个步骤中使用GBDT模型进行回归预测,当然其他的回归方法也可以使用。
GBrank的Python实现
from itertools import combinations
import numpy as np
class Node(object):
def __init__(self, parent, data_index, predict_value):
self.parent = parent
self.data_index = data_index
self.predict_value = predict_value
self.left = None
self.right = None
self.split_feature_index = None
self.split_feature_value = None
class RegressionTree(object):
def __init__(self, min_data_in_leaf):
self.min_data_in_leaf = min_data_in_leaf
self.tree = None
def fit(self, X, ys):
tree = Node(None, np.arange(X.shape[0]), np.mean(ys))
cand_leaves = [tree]
while len(cand_leaves) != 0:
min_squared_error = np.inf
for leaf in cand_leaves:
X_target = X[leaf.data_index]
ys_target = ys[leaf.data_index]
for d in range(X_target.shape[1]):
argsort = np.argsort(X_target[:, d])
# 以最小二乘法进行分割
for split in range(1, argsort.shape[0]):
#[0,split),[split,N_target)で分割
tmp_left_data_index = argsort[:split]
tmp_right_data_index = argsort[split:]
left_predict = np.mean(ys_target[tmp_left_data_index])
left_squared_error = np.sum((ys_target[tmp_left_data_index] - left_predict)**2)
right_predict = np.mean(ys_target[tmp_right_data_index])
right_squared_error = np.sum((ys_target[tmp_right_data_index] - right_predict)**2)
squared_error = left_squared_error + right_squared_error
if squared_error< min_squared_error:
min_squared_error = squared_error
target_leaf = leaf
left_data_index = leaf.data_index[tmp_left_data_index]
right_data_index = leaf.data_index[tmp_right_data_index]
split_feature_index = d
split_feature_value = X_target[:, d][tmp_right_data_index[0]]
if min_squared_error == np.inf:
break
cand_leaves.remove(target_leaf)
if left_data_index.shape[0] < self.min_data_in_leaf or right_data_index.shape[0] < self.min_data_in_leaf:
continue
left_node = Node(target_leaf, np.sort(left_data_index), np.mean(ys[left_data_index]))
right_node = Node(target_leaf, np.sort(right_data_index), np.mean(ys[right_data_index]))
target_leaf.split_feature_index = split_feature_index
target_leaf.split_feature_value = split_feature_value
target_leaf.left = left_node
target_leaf.right = right_node
if left_node.data_index.shape[0] > 1:
cand_leaves.append(left_node)
if right_node.data_index.shape[0] > 1:
cand_leaves.append(right_node)
self.tree = tree
def predict(self, X):
ys_predict = []
for xs in X:
node = self.tree
while node.left is not None and node.right is not None:
if xs[node.split_feature_index] < node.split_feature_value:
node = node.left
else:
node = node.right
ys_predict.append(node.predict_value)
return np.array(ys_predict)
class GBrank(object):
def __init__(self, n_trees, min_data_in_leaf, sampling_rate, shrinkage, tau=0.5):
self.n_trees = n_trees
self.min_data_in_leaf = min_data_in_leaf
self.sampling_rate = sampling_rate
self.shrinkage = shrinkage
self.tau = tau
self.trees = []
def fit(self, X, ys, qid_lst):
for n_tree in range(self.n_trees):
if n_tree == 0:
rt = RegressionTree(1)
rt.fit(np.array([[0]]), np.array([0]))
self.trees.append(rt)
continue
target_index = np.random.choice(
X.shape[0],
int(X.shape[0] * self.sampling_rate),
replace=False
)
X_target = X[target_index]
ys_target = ys[target_index]
qid_target = qid_lst[target_index]
ys_predict = self._predict(X_target, n_tree)
qid_target_distinct = np.unique(qid_target)
X_train_for_n_tree = []
ys_train_for_n_tree = []
for qid in qid_target_distinct:
X_target_in_qid = X_target[qid_target == qid]
ys_target_in_qid = ys_target[qid_target == qid]
ys_predict_in_qid = ys_predict[qid_target == qid]
for left, right in combinations(enumerate(zip(ys_target_in_qid, ys_predict_in_qid)), 2):
ind_1, (ys_target_1, ys_predict_1) = left
ind_2, (ys_target_2, ys_predict_2) = right
if ys_target_1< ys_target_2:
ys_target_1, ys_target_2 = ys_target_2, ys_target_1
ys_predict_1, ys_predict_2 = ys_predict_2, ys_predict_1
ind_1, ind_2 = ind_2, ind_1
if ys_predict_1< ys_predict_2 + self.tau:
X_train_for_n_tree.append(X_target_in_qid[ind_1])
ys_train_for_n_tree.append(ys_target_in_qid[ind_1] + self.tau)
X_train_for_n_tree.append(X_target_in_qid[ind_2])
ys_train_for_n_tree.append(ys_target_in_qid[ind_2] - self.tau)X_train_for_n_tree = np.array(X_train_for_n_tree)
ys_train_for_n_tree = np.array(ys_train_for_n_tree)
rt = RegressionTree(self.min_data_in_leaf)
rt.fit(X_train_for_n_tree, ys_train_for_n_tree)
self.trees.append(rt)
def _predict(self, X, n_predict_trees):
predict_lst_by_trees = [self.trees[n_tree].predict(X) for n_tree in range(n_predict_trees)]
predict_result = predict_lst_by_trees[0]
for n_tree in range(1, n_predict_trees):
predict_result = (n_tree * predict_result + self.shrinkage * predict_lst_by_trees[n_tree]) / (n_tree + 1)
return predict_result
def predict(self, X):
return self._predict(X, len(self.trees))
算法总结
$h(x)$为最终的排序函数,GBRank在训练时每次迭代中将$h_k(x)$的排序结果与真实结果不一样的样本(就是分错的样本)单独拿出来做训练样本,并且其训练目标为pair的另一个预测值作为回归目标,非常巧妙。
此时重新看这个GBRank模型与AdaBoost、GBT其实很大同小异,都是将上一次训练中分错的样本再拿来训练,也是一个提升的模型
在其paper中的实验结果也是要略好于$RankSvm$,但是其比较疼的时其训练还是比较复杂的,或者说比较耗时,其预测也会比较麻烦一点,所以使用时得慎重~
参考链接: