文章内容如有错误或排版问题,请提交反馈,非常感谢!
分治法概念
分治法(divide-and-conquer)字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。分治有两个特点:
- 子问题相互独立且与原问题形式相同
- 反复分治,使划分得到的子问题小到不能再分时,直接对其求解
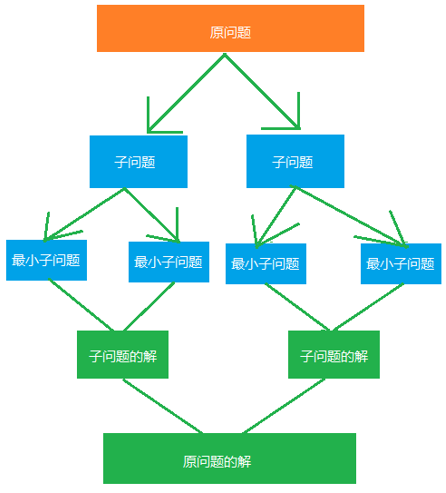
分治法所能解决的问题一般具有以下特征:
- 该问题的规模缩小到一定程度就可以容易的解决。
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构的性质。
- 利用该问题分解出的子问题的解可以合并为该问题的解(关键性质)
- 该问题所分解出的各个子问题最好是相互独立的,即子问题之间不包含公共的子问题。
其中:
- 第一条特征是绝大多数问题都能满足的,因为计算复杂性一般随着规模的减小而降低。
- 第二条特征是应用分治法的前提,它也是大多数问题可以满足的,此特征反映了递归思想的应用。
- 第三条特征是关键,能否利用分治法完全取决于问题是否具有第三条特征。如果具备了第一条特征和第二条特征,而子问题的解不可以合并,则可以考虑贪心算法或动态规划。
- 第四条特征涉及分治法的效率,如果各子问题不是独立的,则分治法要做许多不必要的工作,重复地解公共的子问题,此时虽然可用分治法,但一般用动态规划法较好。
分治模式在每一层递归上都有三个步骤:
- 分解(Divide):将原问题分解为若干个规模较小、相互独立、与原问题形式相同的子问题。
- 解决(Conquer):若子问题规模较小而容易求解则直接求解,否则递归的解决各个子问题。
- 合并(Combine):将各个子问题的解合并为原问题的解。
分治法的一般算法框架如下:
divide_and_conquer(problem)
{
if(|problem|<n) adhoc(problem); /*解决小规模的问题*/
divide Problem into smaller subinstances P1,P2,....Pk; /*分解问题*/
for(i=1;i<=k(子问题个数);++i){
result[i]=divide_and_conquer(P[i]); /*递归的解各个子问题*/
}
return merge(result[1]...result[k]); /*将各个子问题的解合并为原问题的解*/
}
分治法求解的一些经典问题:
- 二分搜索
- 大整数乘法
- Strassen矩阵乘法
- 棋盘覆盖
- 合并排序
- 快速排序
- 线性时间选择
- 最接近点对问题
- 循环赛日程表
- 汉诺塔
分治法的典型实例
二分搜索
问题描述:给定已按照升序排列好的n个元素a[0:n-1],现在要在这n个元素中找出一特定元素。
问题分析:采用分治法的思想,充分利用元素之间已经存在的次序关系,将序列划分为两个个数相同的左右两个部分,取最中间的元素和x进行比较,如果等于中间的元素就找到,如果不等于,就递归的在左边(x<中间值)或者右边(x>中间值)二分查找。
注意事项:对于二分查找,一般需要建立两个不变性:
- 当前待查找序列,肯定包含目标元素
- 每次待查找序列的规模都会变小。
Python示例:
# -*- coding: utf-8 -*-
def binary_search(array, t):
low = 0
height = len(array)-1
while low < height:
mid = low + (height-low)//2
# 用mid=(begin+end)//2是有溢出危险的,对于一个规模足够大的数组(极端假设为2147483647个元素),那么在对后半部(2/n~n)取mid时,使用mid=(end+start)/2溢出(结果会得到一个负数)
if array[mid] < t:
low = mid + 1
elif array[mid] > t:
height = mid - 1
else:
return array[mid]
return -1
if __name__ == "__main__":
print(binary_search([1,2,3,34,56,57,78,87],57))
快速排序
快速排序(Quicksort),是一种排序算法,最坏情况复杂度:Ο(n2),最优时间复杂度:Ο(nlogn),平均时间复杂度:Ο(nlogn)。快速排序的基本思想也是用了分治法的思想:找出一个元素X,在一趟排序中,使X左边的数都比X小,X右边的数都比X要大。然后再分别对X左边的数组和X右边的数组进行排序,直到数组不能分割为止。
快速排序的基本思想:设当前待排序的无序区为R[low..high],利用分治法可将快速排序的基本思想描述为:
- 分解:在R[low..high]中任选一个记录作为基准(Pivot),以此基准将当前无序区划分为左、右两个较小的子区间R[low..pivotpos-1)和R[pivotpos+1..high],并使左边子区间中所有记录的关键字均小于等于基准记录(不妨记为pivot)的关键字key,右边的子区间中所有记录的关键字均大于等于pivot.key,而基准记录pivot则位于正确的位置(pivotpos)上,它无须参加后续的排序。(注意:划分的关键是要求出基准记录所在的位置pivotpos。划分的结果可以简单地表示为(注意pivot=R[pivotpos]):R[low..pivotpos-1].keys≤R[pivotpos].key≤R[pivotpos+1..high].keys,其中low≤pivotpos≤high。)
- 求解:通过递归调用快速排序对左、右子区间R[low..pivotpos-1]和R[pivotpos+1..high]快速排序。
- 组合:因为当”求解”步骤中的两个递归调用结束时,其左、右两个子区间已有序。对快速排序而言,”组合”步骤无须做什么,可看作是空操作。
Python实现:
#-*- coding: utf-8 -*-
# 方法1
def quickSort(arr):
less = []
pivotList = []
more = []
if len(arr) <= 1:
return arr
else:
pivot = arr[0] # 将第一个值做为基准
for i in arr:
if i< pivot:
less.append(i)
elif i > pivot:
more.append(i)
else:
pivotList.append(i)
less = quickSort(less) # 得到第一轮分组之后,继续将分组进行下去。
more = quickSort(more)
return less + pivotList + more
# 方法2
# 分为<, >, = 三种情况,如果分为两种情况的话函数调用次数会增加许多,以后几个好像都有相似的问题
# 如果测试1000个100以内的整数,如果分为<, >= 两种情况共调用函数1801次,分为<, >, = 三种情况,共调用函数201次
def qsort(L):
return (
qsort([y for y in L[1:] if y< L[0]])
+ L[:1] + [y for y in L[1:] if y == L[0]]
+ qsort([y for y in L[1:] if y > L[0]])
) if len(L) > 1 else L
# 方法3
# 基本思想同上,只是写法上又有所变化
# def qsort(list):
# if not list:
# return []
# else:
# pivot = list[0]
# less = [x for x in list if x< pivot]
# more = [x for x in list[1:] if x >= pivot]
# return qsort(less) + [pivot] + qsort(more)
# 方法4
from random import *
def qSort(a):
if len(a) <= 1:
return a
else:
q = choice(a) # 基准的选择不同于前,是从数组中任意选择一个值做为基准
return qSort([elem for elem in a if elem< q]) + [q] * a.count(q) + qSort([elem for elem in a if elem > q])
# 方法5
# 这个最狠了,一句话搞定快速排序,瞠目结舌吧。
qs = lambda xs: \
((len(xs) <= 1 and [xs]) or [
qs([x for x in xs[1:] if x< xs[0]]) + [xs[0]] + qs([x for x in xs[1:] if x >= xs[0]])])[
0]
if __name__ == "__main__":
a = [4, 65, 2, -31, 0, 99, 83, 782, 1]
print(quickSort(a))
print(qsort(a))
print(qSort(a))
print(qs(a))