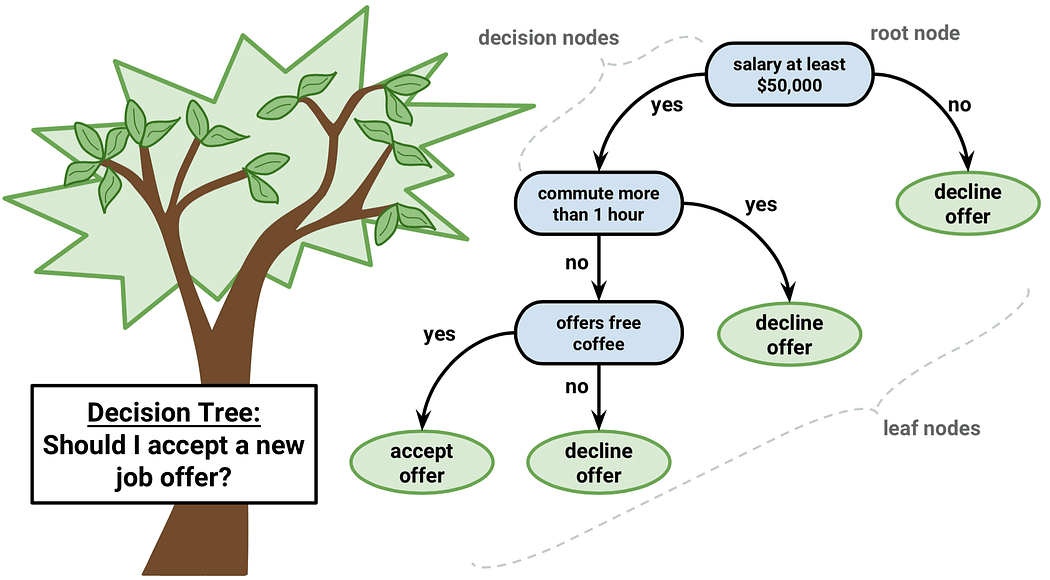
在数据分析或算法模型搭建时,经常会遇到将连续变量转化为类别分箱的场景。用的分箱方法有等宽分箱、等频分箱、聚类分箱和基于决策树的分箱等。今天要分享的是基于组别间差异的决策树分箱方法。
代码实现
import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from scipy import stats
def get_balanced_bin_rules(feature_values, target, sample_weights, max_bins=5, alpha=0.05, beta=0.01, gamma=0.1):
"""
计算平衡分箱的分割规则,使用单层决策树进行自动分割。
:param feature_values: pd.Series, 需要分箱的特征值
:param target: pd.Series, 目标变量(分类)
:param sample_weights: pd.Series, 样本权重
:param max_bins: int, 最大分箱数
:param alpha, beta, gamma: float, 分箱控制参数
:return: list, 分箱边界(不包含无穷大)
"""
if max_bins< 2 or feature_values.nunique() <= 1:
return []
# 训练单层决策树
X = feature_values.values.reshape(-1, 1)
target_count = target.nunique()
min_impurity_decrease = (alpha / max_bins) + (beta / np.sqrt(target_count))
min_weight_frac = (gamma / max_bins) * np.log1p(target_count)
clf = DecisionTreeClassifier(
max_depth=1,
min_impurity_decrease=round(min_impurity_decrease, 4),
min_weight_fraction_leaf=round(min_weight_frac, 4)
)
clf.fit(X, target, sample_weight=sample_weights)
if clf.tree_.node_count<= 1: # 决策树未分裂
return []
threshold = clf.tree_.threshold[0]
left_idx, right_idx = feature_values<= threshold, feature_values > threshold
# 计算子节点的权重
left_weight, right_weight = sample_weights[left_idx].sum(), sample_weights[right_idx].sum()
if left_weight< min_weight_frac or right_weight< min_weight_frac:
return []
# 递归处理左右子树
left_rules = get_balanced_bin_rules(feature_values[left_idx], target[left_idx], sample_weights[left_idx],
max_bins-1, alpha, beta, gamma)
right_rules = get_balanced_bin_rules(feature_values[right_idx], target[right_idx], sample_weights[right_idx],
max_bins-1, alpha, beta, gamma)
return sorted(left_rules + [threshold] + right_rules)
def generate_labels(segment_df, full_df, features, bin_edges):
"""
计算各分箱的TGI指数,并生成标签。
:param segment_df: pd.DataFrame, 目标分组样本
:param full_df: pd.DataFrame, 全样本
:param features: list, 需要计算的特征列表
:param bin_edges: dict, 每个特征的分箱边界
:return: str, 生成的标签信息
"""
labels = []
segment_samples = len(segment_df)
def adjust_expected(expected, observed_sum):
"""调整期望值,使其与观测值总和保持一致"""
if expected.sum() == 0:
return expected
return expected * (observed_sum / expected.sum())
for feature in features:
bins = bin_edges.get(feature, [])
if len(bins) < 2:
continue
# 生成分箱标签
thresholds = [t for t in bins[1:-1] if not np.isinf(t)]
bin_labels = (["≤" + f"{thresholds[0]:.2f}"] +
[f"{thresholds[i-1]:.2f}-{thresholds[i]:.2f}" for i in range(1, len(thresholds))] +
[">" + f"{thresholds[-1]:.2f}"]) if thresholds else ["全部"]
try:
# 计算分箱频率
segment_binned = pd.cut(segment_df[feature], bins=bins, labels=bin_labels, include_lowest=True, right=False)
observed = segment_binned.value_counts().reindex(bin_labels, fill_value=0)
full_binned = pd.cut(full_df[feature], bins=bins, labels=bin_labels, include_lowest=True, right=False)
full_counts = full_binned.value_counts().reindex(bin_labels, fill_value=0)
if full_counts.sum() == 0 or observed.sum() == 0:
continue
expected = adjust_expected(full_counts / full_counts.sum() * observed.sum(), observed.sum())
expected = expected.clip(lower=5) # 确保卡方检验要求
valid_mask = (expected >= 5) & (observed >= 5)
if valid_mask.sum() < 2:
continue
expected = adjust_expected(expected[valid_mask], observed[valid_mask].sum())
chi2, p_value = stats.chisquare(observed[valid_mask], expected)
# 生成标签
if p_value< 0.05:
for bin_label in observed.index[valid_mask]:
vendor_ratio = observed[bin_label] / segment_samples
base_ratio = (full_counts[bin_label] / full_counts.sum()) if full_counts.sum() > 0 else 0
tgi = int(round((vendor_ratio / base_ratio) * 100)) if base_ratio > 0 else 999
icon = '🔥' if tgi >= 150 else '↑↑' if tgi >= 120 else '🥶' if tgi<= 50 else '↓↓' if tgi<= 80 else '--'
labels.append(f"{feature}_{bin_label}({vendor_ratio:.0%}, TGI={tgi}{icon})")
except Exception as e:
print(f"[WARN] 特征 {feature} 计算异常: {str(e)}")
return "|".join(labels)
def get_balanced_bin_and_labels(df, target, bin_config):
"""计算所有特征的分箱边界,并生成标签"""
class_counts = df[target].value_counts()
class_weight = {k: len(df) / (len(class_counts) * v) for k, v in class_counts.items()}
sample_weights = df[target].map(class_weight)
bin_edges = {}
for feature, config in bin_config.items():```python
try:
if isinstance(config, list):
edges = sorted(config)
else:
max_bins = config if isinstance(config, int) else 5
thresholds = get_balanced_bin_rules(df[feature], df[target], sample_weights, max_bins)
edges = sorted([-np.inf] + [t for t in thresholds if not np.isinf(t)] + [np.inf])
bin_edges[feature] = edges
except Exception as e:
print(f"[ERROR] {feature} 分箱失败: {str(e)}")
bin_edges[feature] = [-np.inf, np.inf]
results = {segment: generate_labels(df[df[target] == segment], df, bin_config.keys(), bin_edges)
for segment in df[target].unique()}
return bin_edges, results
if __name__ == '__main__':
df = pd.read_csv("data/data.csv")
target = '渠道'
bin_config = {'时长': [0, 30, 90, np.inf], '金额': 'auto', '距离': 6}
bin_edges, segment_labels = get_balanced_bin_and_labels(df, target, bin_config)
print("\n分箱边界:")
for dim, edges in bin_edges.items():
print(f"{dim}: {[round(e, 2) if not np.isinf(e) else e for e in edges]}")
print("\n特征分布:")
for segment, label in segment_labels.items():
print(f"{segment}: {label}")
该代码实现了一个自动化特征分箱及标签生成系统,主要用于分析目标群体在多个特征上的分布差异,适用于客户分群、特征重要性分析等场景。其核心逻辑分为分箱规则计算与标签生成两大部分,具体功能如下:
分箱规则计算(get_balanced_bin_rules函数)
功能:通过递归单层决策树生成平衡分箱规则,将连续特征离散化为具有统计意义的区间。
逻辑流程:
- 初始化检查:若最大分箱数不足或特征唯一值过少,直接返回空列表。
- 决策树训练:
- 使用单层决策树(max_depth=1)寻找最佳分割点。
- 动态计算分割参数min_impurity_decrease和min_weight_fraction_leaf,结合alpha(纯度下降阈值系数)、beta(目标类别数调节项)、gamma(最小样本权重系数)控制分箱粒度和样本均衡性。
- 递归分割:
- 根据决策树分割阈值将数据分为左右子集。
- 检查子节点的样本权重是否满足最小要求(避免过少样本)。
- 递归处理左右子集,合并分箱边界,生成最终有序的分割点列表(如[0,30,90])。
示例输出:特征"时长"可能被分为[-inf,0,30,90,inf]四个区间。
标签生成(generate_labels函数)
功能:基于分箱结果计算TGI指数(目标群体指数),并通过卡方检验生成描述性标签,标识目标群体特征显著差异。
逻辑流程:
- 分箱处理:
- 对目标群体(segment_df)和全体样本(full_df)进行分箱,统计各箱样本占比。
- 统计检验:
- 计算期望频数,调整其总和与观测值一致。
- 应用卡方检验(chisquare)判断分布差异显著性(p_value<0.05视为显著)。
- 标签生成:
- 计算TGI指数:(目标群体占比/全体样本占比)*100,反映特征箱的倾向性。
- 根据TGI值添加图标(如🔥表示TGI≥150),生成易读标签(如"金额_≤00(25%,TGI=200🔥)")。
应用场景:识别某营销渠道用户消费金额在30元以下的比例显著高于整体用户(TGI=200),提示该特征对渠道选择的重要性。
整合流程(get_balanced_bin_and_labels函数)
功能:协调分箱与标签生成,支持手动配置与自动分箱混合模式。
逻辑流程:
- 样本权重计算:根据目标类别频数逆权重平衡样本(避免类别不平衡影响分箱)。
- 分箱配置解析:
- 若配置为列表(如[0,30,90,inf]),直接使用预设分箱。
- 若配置为整数或"auto",调用get_balanced_bin_rules自动分箱。
- 结果聚合:对每个目标类别生成特征分布标签,汇总分箱边界及标签结果。
配置示例:
bin_config={'时长':[0,30,90,np.inf],'金额':'auto','距离':6}表示:"时长"手动分箱,其他特征自动分箱("金额"自适应,"距离"最多6箱)。
输出示例
分箱边界:
时长:[-inf,0,30,90,inf] 金额:[-inf,50,200,500,inf]
特征标签:
渠道A:金额_≤50.00(20%,TGI=150↑↑)|距离_0-5km(15%,TGI=120↑↑) 渠道B:时长_>90.00(10%,TGI=50🥶)
核心价值
- 自动化分箱:结合统计方法与业务参数,避免人工划分的主观性。
- 显著性验证:通过假设检验确保分箱差异具有统计意义。
- 业务可解释性:TGI与图标直观反映特征重要性,辅助决策制定。
适用于金融风控(识别高风险客户特征)、零售营销(定位高潜力用户群)等需精细化特征分析的场景。
代码解释
单层决策树
在代码中使用单层决策树(max_depth=1)的核心原因在于通过有监督学习寻找最优分箱边界,同时平衡分箱的统计意义与计算效率。以下是具体分析:
功能目标导向:模拟“最佳单次分割”
- 核心需求:分箱需要将连续特征划分为多个区间,使每个区间内的样本在目标变量上具有显著差异。
- 单层决策树的作用:
- 仅进行一次分裂(单层),找到使目标变量纯度提升最大的分割点(如基尼不纯度或信息增益)。
- 相当于在全局范围内选择最有利于区分目标类别的单一分割点,确保每次分割的统计显著性。
- 对比无监督分箱(如等频、等宽):
- 无监督分箱可能忽略目标变量的分布,导致分箱后的区间对建模无意义。
- 单层决策树通过目标变量指导分割,使分箱结果与业务目标直接关联。
```
递归分箱的构建基础
- 递归逻辑:每次分割后,对左右子集递归调用分箱函数,逐步细化分箱。
- 单层决策树的适配性:
- 每个递归步骤只需关注当前数据子集的最优单次分割,无需复杂树结构。
- 通过参数(如 max_bins)控制总箱数,避免过拟合。
- 示例:
- 初始数据分割为 [≤阈值, >阈值]。
- 对左侧子集递归分割为 [≤子阈值, >子阈值],最终形成 [≤A, A-B, >B] 等规则。
统计控制与效率优化
- 参数动态计算:
- min_impurity_decrease(最小纯度提升)和 min_weight_fraction_leaf(最小叶子权重)由 alpha, beta, gamma 动态控制。
- 确保分割后的子节点满足统计显著性要求(如卡方检验前置条件)。
- 计算效率优势:
- 单层决策树的训练时间复杂度为O(n),远低于深层树(O(n log n))。
- 适合高维特征和大规模数据场景。
与业务场景的深度契合
- 业务可解释性:单次分割的阈值可直接解释为关键业务分界点(如“金额 > 1000”代表高消费群体)。
- 兼容显著性检验:通过卡方检验验证分箱后各区间的目标分布差异,单层决策树的分割天然支持这一过程。
- 示例场景:在金融风控中,通过单层决策树找到“逾期次数 ≥ 2 次”作为分箱阈值,直接关联违约风险。
与其他方法的对比
| 方法 | 优势 | 劣势 | 适用场景 |
| 单层决策树(本代码) | 有监督、统计可控、高效 | 依赖目标变量分布 | 需目标驱动的分箱(如 TGI 计算) |
| 等频/等宽分箱 | 无需目标变量、简单 | 忽略目标变量关联性 | 探索性分析 |
| 卡方分箱 | 自动合并相似区间、统计驱动 | 计算复杂度高、可能过度合并 | 高基数特征分箱 |
| 聚类分箱 | 捕捉数据分布模式 | 无监督、结果难以解释 | 非结构化特征分析 |
总结
使用 max_depth=1 的单层决策树,本质是以目标变量为导向,通过递归分割实现高效、可控、可解释的特征分箱。它平衡了以下需求:
- 有监督性:确保分箱与业务目标强相关。
- 统计严谨性:通过动态参数避免过拟合和无效分割。
- 计算效率:适合大规模特征工程。
- 可解释性:直接输出业务可理解的阈值规则。
这种方法特别适合需要生成 TGI 指数、特征画像标签等强业务关联的场景,是自动化特征工程中的经典实践。
卡方检验与卡方分箱
在代码中使用卡方检验(Chi-square Test)而非卡方分箱(Chi-square Binning),是由两者的功能定位和应用场景差异决定的。以下是具体分析:
核心区别:目的与阶段不同
| 方法 | 卡方分箱 | 卡方检验(本代码) |
| 目标 | 特征分箱(合并区间) | 验证分箱显著性(评估分布差异) |
| 阶段 | 分箱过程(预处理阶段) | 分箱后评估(后验分析阶段) |
| 输入数据 | 连续特征 + 目标变量 | 已分箱的离散特征 + 目标群体分布 |
| 输出 | 分箱边界 | p 值、TGI 指数、显著性标签 |
为什么选择卡方检验而非卡方分箱?
分箱方法已确定:决策树分箱替代卡方分箱
- 卡方分箱的局限性:
- 通过合并相邻区间实现分箱,可能过度依赖统计量而忽略业务解释性。
- 需预设最小样本量或卡方阈值,参数调整复杂。
- 决策树分箱的优势:
- 直接以目标变量为导向,最大化分箱的预测能力(如基尼不纯度)。
- 支持递归分割,通过 max_bins 等参数灵活控制分箱数量。
卡方检验的定位:后验显著性验证
- 核心需求:
- 分箱完成后,需验证目标群体(如某渠道用户)在各分箱中的分布是否显著偏离全量样本。
- 生成业务可解释的标签(如“TGI=150↑↑”)。
- 卡方检验的作用:
- 判断观测频数(目标群体分箱分布)与期望频数(全量样本分布)的差异是否由随机因素导致。
- 通过 p_value< 0.05 筛选显著差异分箱,避免生成无意义的标签。
业务场景适配性
- TGI 指数与显著性联动:
- TGI 反映目标群体的倾向性(如 TGI=120 表示该分箱用户占比比全量高 20%)。
- 卡方检验验证这种倾向性是否具有统计意义,避免误将随机波动视为业务结论。
- 示例:
- 若某分箱的 TGI=150,但 p_value=0.1(不显著),则该分箱可能是偶然现象,无需生成标签。
- 若 TGI=120 且 p_value=0.01,则可标记为显著特征(如“↑↑”)。
卡方分箱不适用本场景的深层原因
功能冲突
- 卡方分箱的目标:合并相似区间以降低特征维度。
- 本代码的目标:生成可解释的显著差异标签,而非压缩特征维度。
与决策树分箱的互补性
- 决策树分箱:通过目标变量指导分割,确保分箱与业务强相关。
- 卡方检验:验证分箱后的统计显著性,二者形成完整工作流:决策树分箱 → 递归细化 → 卡方检验 → 生成标签
工程实现复杂度
- 卡方分箱需迭代合并区间,可能引入额外参数(如最大分箱数、最小卡方值),增加代码复杂度。
- 决策树分箱 + 卡方检验组合更轻量,且分箱与验证步骤解耦,便于维护。
总结
代码中使用卡方检验而非卡方分箱,本质是“分箱方法”与“分箱验证”的分工:
- 分箱方法:决策树分箱(有监督、递归、业务可解释)。
- 分箱验证:卡方检验(统计显著性筛选)。
这种分工的优势在于:
- 业务导向:决策树分箱直接关联目标变量,生成对业务有预测力的分箱。
- 统计严谨:卡方检验过滤噪声,确保标签的可靠性。
- 灵活性:可替换分箱方法(如改用卡方分箱),而检验逻辑保持不变。
若强行替换为卡方分箱,反而会导致以下问题:
- 分箱过程与后续的TGI计算、标签生成逻辑脱节。
- 无法直接验证分箱后的统计显著性,降低标签的可信度。
卡方检验的目的
在代码中使用卡方检验的核心目的是验证目标群体与全量样本在特征分箱上的分布差异是否具有统计显著性,从而筛选出对业务有实际意义的分箱标签。以下是具体原因和应用逻辑:
卡方检验的适用场景
卡方检验(Chi-square test)是一种非参数检验方法,专门用于比较分类变量的观测频数与期望频数之间的差异。在本代码中,分箱后的特征本质上是将连续变量转换为有序分类变量,卡方检验的适用性体现在以下方面:
- 数据形态匹配:
- 分箱后的特征为离散区间(如“金额≤50元”),属于分类变量。
- 目标群体的分布(观测频数)与全量样本的分布(期望频数)均以频数形式存在。
- 检验目标明确:
- 零假设(H₀):目标群体在各分箱中的分布与全量样本无显著差异。
- 备择假设(H₁):目标群体的分布与全量样本存在显著差异。
- 通过拒绝H₀,筛选出具有业务意义的特征分箱(如某渠道用户显著集中在高消费区间)。
代码中的卡方检验实现细节
在 generate_labels 函数中,卡方检验的应用步骤如下:
频数统计与期望值调整
# 计算观测频数(目标群体分箱分布) observed = segment_binned.value_counts().reindex(bin_labels, fill_value=0) # 计算全量样本分箱分布作为期望基准 full_counts = full_binned.value_counts().reindex(bin_labels, fill_value=0) expected = full_counts / full_counts.sum() * observed.sum() # 调整期望值总和与观测值一致(避免比例误差) expected = adjust_expected(expected, observed.sum()) expected = expected.clip(lower=5) # 确保卡方检验有效性
关键操作:
- 将全量样本的分箱比例作为期望基准,按目标群体的样本量缩放。
- 通过 adjust_expected 保证期望频数总和与观测值一致。
- 对期望频数进行下限截断(clip(lower=5)),满足卡方检验的适用条件。
显著性筛选与标签生成
# 执行卡方检验(仅保留有效分箱)
valid_mask = (expected >= 5) & (observed >= 5)
chi2, p_value = stats.chisquare(observed[valid_mask], expected[valid_mask])
# 根据 p 值生成标签(p< 0.05 视为显著差异)
if p_value< 0.05:
for bin_label in observed.index[valid_mask]:
# 计算 TGI 指数并生成标签(如"金额_≤50.00(25%,TGI=200🔥)")
...
筛选逻辑:
- 仅保留期望频数≥5且观测频数≥5的分箱(避免检验失真)。
- 通过 p_value< 0.05 判断分布差异是否显著,决定是否生成标签。
为什么选择卡方检验而非其他方法?
与 TGI 指标的业务逻辑一致
TGI(Target Group Index):衡量目标群体在某一特征上的倾向性,公式为:
$$\text{TGI}=\frac{\text{目标群体占比}}{\text{全量样本占比}}\times100$$
卡方检验直接验证“占比差异是否显著”,与 TGI 的计算逻辑天然契合。
与其他方法的对比
| 方法 | 适用场景 | 在本代码中的局限性 |
| t检验/ANOVA | 连续变量 vs 分类变量 | 分箱后数据为分类变量,不适用 |
| KS检验 | 连续分布差异检验 | 需连续数据,且仅支持两组比较 |
| Fisher检验 | 小样本 2×2 列联表 | 分箱数可能大于 2,且样本量较大 |
| 卡方检验 | 多分类频数比较,大样本 | 完全匹配分箱后的频数比较需求 |
业务意义与输出示例
业务价值
- 识别关键特征:通过卡方检验筛选出与目标群体强相关的分箱(如“渠道A用户显著集中在‘金额≤50元’”)。
- 支持决策:标记高 TGI 分箱(如 TGI=200🔥),指导资源倾斜(如针对低消费群体设计促销活动)。
输出示例
渠道A: 金额_≤50.00(25%,TGI=200🔥)|距离_0-5km(15%,TGI=120↑↑) 渠道B: 时长_>90.00(10%,TGI=50🥶)
解读:
- 渠道A用户中,25%的人消费金额≤50元,且该群体的 TGI=200(显著高于全量用户2倍)。
- 渠道B用户在“时长>90分钟”的分箱中 TGI=50(显著低于平均水平),提示该群体活跃度低。
总结
使用卡方检验的核心原因是:
- 方法匹配性:分箱后的特征为分类变量,卡方检验是频数差异检验的金标准。
- 业务可解释性:通过显著性筛选避免噪声干扰,确保生成的 TGI 标签具有统计意义。
- 工程兼容性:与递归分箱逻辑无缝衔接,支持自动化流水线处理。
这种方法将统计学严谨性与业务目标结合,为特征分析提供了可靠的技术支撑。
类别权重的计算
在类别不平衡问题中,样本权重的计算旨在平衡各类别在损失函数中的贡献。公式为:权重 = 总样本数 / (类别数 × 该类样本数)
为什么权重计算不使用总样本数 / 该类样本数?
在样本权重计算中,关键目标是让每个类别的总贡献(即所有样本的权重之和)相等,从而避免模型偏向多数类。代码中 len(df) / (len(class_counts) * v) 的设计正是为了实现这一目标,而 len(df) / v 的简化形式会导致权重失衡。
代码公式的核心逻辑
公式含义:class_weight[k] = len(df) / (len(class_counts) * v)
- 总样本数:len(df)
- 类别数量:len(class_counts)
- 当前类别的样本数:v
作用:每个类别的总权重 = 样本数 × 权重
这意味着所有类别的总权重相等(均为总样本数 / 类别数)。
示例:
假设总样本数 100,三分类(类别数 3),各类样本数分别为 10, 20, 70。
- 类别1的权重:100 / (3 × 10) ≈ 3.33 → 总权重 10 × 3.33 ≈ 33.3
- 类别2的权重:100 / (3 × 20) ≈ 1.67 → 总权重 20 × 1.67 ≈ 33.3
- 类别3的权重:100 / (3 × 70) ≈ 0.476 → 总权重 70 × 0.476 ≈ 33.3
所有类别的总权重相等(33.3),模型不会偏向任何类别。
若使用 len(df) / v 会发生什么?
公式含义:class_weight[k] = len(df) / v作用:每个类别的总权重 = 样本数 × 权重
这意味着所有类别的总权重均为总样本数。
问题:
- 总权重未归一化:所有类别的总权重之和为类别数 × 总样本数,这会放大损失函数的值,影响训练稳定性。
- 未考虑类别数量:在多分类任务中,若类别数较多,损失函数的计算会严重失衡。
示例:
总样本数 100,三分类(类别数 3),各类样本数分别为 10, 20, 70。
- 类别1的权重:100 / 10 = 10 → 总权重 10 × 10 = 100
- 类别2的权重:100 / 20 = 5 → 总权重 20 × 5 = 100
- 类别3的权重:100 / 70 ≈ 1.43 → 总权重 70 × 1.43 ≈ 100
所有类别的总权重均为 100,但损失函数的总权重为 300(3 × 100),明显偏离实际样本分布。
与 Scikit-learn 的一致性
Scikit-learn 的 class_weight='balanced' 使用与原公式相同的逻辑:
权重 = 总样本数 / (类别数 × 该类样本数)
决策树参数
使用决策树递归生成平衡分箱规则,其中两个关键参数min_impurity_decrease和min_weight_fraction_leaf控制分箱过程的终止条件。它们的作用是平衡模型的复杂性与分箱的合理性,避免过拟合或无效分箱。
- min_impurity_decrease:控制分裂的质量,确保每次分裂显著提升分类性能。
- min_weight_fraction_leaf:控制分裂的样本分布,避免生成不具业务意义的分箱。
- 联合作用:在递归分箱过程中,两者共同约束,生成平衡、稳定且可解释的分箱规则。
min_impurity_decrease
定义:该参数表示分裂节点时要求的最小不纯度减少量。若分裂后的不纯度减少量低于此阈值,则放弃分裂。
数学公式:
$$\text{不纯度减少量} = \text{父节点不纯度} - \left(\frac{w_{\text{左}}}{w_{\text{父}}} \cdot \text{左子节点不纯度} + \frac{w_{\text{右}}}{w_{\text{父}}} \cdot \text{右子节点不纯度}\right)$$
其中 w 为节点样本权重之和,不纯度通常用基尼指数或信息熵衡量。
作用:
- 过滤无效分裂:避免对模型性能提升微乎其微的分裂(例如噪声导致的微小改进)。
- 简化分箱规则:确保每次分裂都显著提升分类纯度,生成更有意义的分箱阈值。
推荐值:
- 默认尝试:0.01(适用于基尼不纯度或信息熵的常规范围)。
- 多分类调整:若目标有 6 个类别,由于不纯度计算的基数较大,可略微降低至 0.005 ~ 0.02 之间,以平衡分裂的敏感度。
- 验证方法:通过网格搜索(如 [0.005, 0.01, 0.02])结合交叉验证选择最优值。
min_weight_fraction_leaf
定义:该参数表示叶节点所需的最小加权样本占比。若分裂后任意子节点的权重占比小于此阈值,则放弃分裂。
数学公式:
$$\text{叶节点权重占比} = \frac{\text{叶节点样本权重之和}}{\text{总样本权重}}$$
若任一子节点的权重占比 < min_weight_fraction_leaf,分裂被禁止。
作用:
- 防止样本权重失衡:避免生成样本权重过小的分箱(例如单个高权重样本主导分箱)。
- 保证分箱实用性:确保每个分箱有足够的代表性,适应业务场景需求(如风控模型需避免极端稀疏分箱)。
推荐值:
- 均匀权重:设为 0.05(即每个分箱至少占总权重的 5%)。
- 不均衡权重:若样本权重差异大(如高权重样本占主导),可提高至 0.1 ~ 0.2。
- 业务约束:在需严格避免小分箱的场景(如风控模型),可设为 0.1 以上。
min_impurity_decrease 的自动计算
规则:
- 分箱数越多 (max_bins ↑),允许更小的不纯度减少量,促进分裂。
- 目标类别数越多 (target_count ↑),需更严格的不纯度减少阈值,避免过拟合。
公式:
$$\text{min_impurity_decrease} = \frac{\alpha}{max\_bins} + \frac{\beta}{\sqrt{\text{target_count}}}$$
其中 $\alpha$ 和 $\beta$ 为经验系数(如 $\alpha = 0.1, \beta = 0.05$)。
min_weight_fraction_leaf 的自动计算
规则:
- 分箱数越多 (max_bins ↑),叶节点权重占比阈值需越小,允许更细粒度分箱。
- 目标类别数越多 (target_count ↑),需适当提高权重占比阈值,防止分箱覆盖不足。
公式:
$$\text{min_weight_fraction_leaf} = \frac{\gamma}{max\_bins} \times \log(1 + \text{target_count})$$
其中 $\gamma$ 为经验系数(如 $\gamma = 0.2$)。