ALS(alternating least squares)
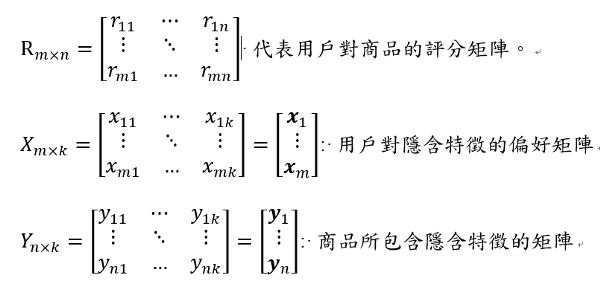
ALS是交替最小二乘的简称。在机器学习中,ALS特指使用交替最小二乘求解的一个协同推荐算法。如:将用户(user)对商品(item)的评分矩阵分解成2个矩阵:
- user对item潜在因素的偏好矩阵(latent factor vector)
- item潜在因素的偏好矩阵
假设有m个user和n个item,所以评分矩阵为R。ALS(alternating least squares)希望找到2个比较低纬度的矩阵(X和Y)来逼近这个评分矩阵R。

$$R_{m\times n}\approx X_{m\times k}\cdot Y_{n\times k}^T$$
ALS的核心就是这样一个假设:打分矩阵是近似低秩的。换句话说,就是一个m*n的打分矩阵可以由分解的两个小矩阵U(m*k)和V(k*n)的乘积来近似。这就是ALS的矩阵分解方法。
为了让X和Y相乘能逼近R,因此我们需要最小化损失函数(loss function),因此需要最小化损失函数,在此定义为平方误差和(Mean square error, MSE)。
$$Loss(X,Y)=\sum_{i,u}^{}(r_{ui}-x_uY_i^T)^2$$
一般损失函数都会需要加入正则化项(Regularization item)来避免过拟合的问题,通常是用L2,所以目标函数会被修改为:
$$Loss(X,Y)=\sum_{i,u}^{}(r_{ui}-x_uY_i^T)^2+\lambda(\sum_{u}^{}||x_u||^2+\sum_{i}^{}||y_i||^2)$$
上面介绍了”最小二乘(最小平方误差)”,但是还没有讲清楚”交替”是怎么回事。因为X和Y都是未知的参数矩阵,因此我们需要用”交替固定参数”来对另一个参数求解。
先固定Y,将loss function对X求偏导,使其导数等于0:
$$\frac{\partial Loss(X,Y)}{\partial x_u}=0\Rightarrow x_u=(\sum_{i}^{}y_i^Ty_i+\lambda I)^{-1}\sum_{i}^{}r_{ui}y_i$$
再固定X,将loss function对Y求偏导,使其导数等于0:
$$\frac{\partial Loss(X,Y)}{\partial y_i}=0\Rightarrow y_i=(\sum_{u}^{}x_u^Tx_u+\lambda I)^{-1}\sum_{u}^{}r_{ui}x_u$$
既然是交替,就会有迭代的模式存在:
- 初始化X,Y
- 利用for u=1,…,n do $\frac{\partial Loss(X,Y)}{\partial x_u}=0$去得到$x_u$
- 利用for i=1,…,m do $\frac{\partial Loss(X,Y)}{\partial y_i}=0$去得到$y_i$
- 重复2和3,不断去更新直到均方根误差RMSE收敛
$$\hat{R}\approx XY^T$$
$$RMSE=\sqrt{\frac{\sum(\hat{R}-R)^2}{N}}$$
ALS-WR(alternating-least-squares with weighted-λ-regularization)
加权正则化交替最小二乘法。上文提到的模型适用于解决有明确评分矩阵的应用场景,然而很多情况下,用户没有明确反馈对商品的偏好,也就是没有直接打分,我们只能通过用户的某些行为来推断他对商品的偏好。比如,在电视节目的推荐的问题中,对电视节目收看次数或时长,这时我们可以推测次数越多看的时间越长,用户的偏好程度越高,但是对于没有收看的节目,可能是用户不知道该节目,或者没有途径获取节目,我们不能确定的推测用户不喜欢该节目,ALS-WR通过置信度权重来解决这些问题:对于更确信用户偏好的项赋予较大的权重,对于没有反馈的项赋予较小的权重。
损失函数为:
$${Loss}_{ALS-WR}(X,Y)=\sum_{i,u}c_{ui}(p_{ui}-x_{u}y_{i}^{T})^{2}+\lambda(\sum_{u}||x_{u}||^{2}+\sum_{i}||y_{i}||^{2})$$
$$P_{m\times n}=\left[\begin{array}{ccc}p_{11}&\cdots&p_{1n}\\\vdots&\ddots&\vdots\\p_{m1}&\cdots&p_{mn}\end{array}\right],p_{ui}=\left\{\begin{array}{cc}1&if r_{ui}>0\\0&if r_{ui}=0\end{array}\right.$$
$$C_{m\times n}=\left[\begin{array}{ccc}c_{11}&\cdots&c_{1n}\\\vdots&\ddots&\vdots\\c_{m1}&\ldots&c_{mn}\end{array}\right]=\left[\begin{array}{ccc}1+\alpha r_{11}&\cdots&1+\alpha r_{1n}\\\vdots&\ddots&\vdots\\1+\alpha r_{m1}&\ldots&1+\alpha r_{mn}\end{array}\right],c_{ui}=1+\alpha r_{ui}$$
其中,$r_{ui}$表示原始量化值,比如观看电影的时间;$\alpha$表示根据用户行为所设置的信任度
小结
在实际应用中,由于待分解的矩阵常常是非常稀疏的,与SVD相比,ALS能有效的解决过拟合问题。基于ALS的矩阵分解的协同过滤算法的可扩展性也优于SVD。与随机梯度下降的求解方式相比,一般情况下随机梯度下降比ALS速度快;但有两种情况ALS更优于随机梯度下降:
- 当系统能够并行化时,ALS的扩展性优于随机梯度下降法。
- ALS-WR能够有效的处理用户对商品的隐式反馈的数据
ALS算法的缺点在于:
- 它是一个离线算法。
- 无法准确评估新加入的用户或商品。这个问题也被称为冷启动问题。
参考链接: