层次聚类改进算法之BIRCH

BIRCH算法简介

BIRCH算法的全称是 Balanced Iterative Reducing and Clustering using Hierarchies，它使用聚类特征来表示一个簇，使用聚类特征树（CF-树）来表示聚类的层次结构，算法思路也是“自底向上”的。

BIRCH算法相比Agglomerative 层级算法 具有如下特点：

• 解决了 Agglomerative 算法不能撤销先前步骤的工作的缺陷
• CF-树只存储原始数据的特征信息，并不需要存储原始数据信息，内存开销上更优
• BIRCH算法只需要遍历一遍原始数据，而 Agglomerative 算法在每次迭代都需要遍历一遍数据，所以 BIRCH 在性能也优于 Agglomerative
• BIRCH 是一种增量聚类方法，针对每一个点的聚类决策都是基于当前已经处理过的数据点，而不是全局的数据点。支持对流数据的聚类，BIRCH 一开始并不需要所有的数据

BIRCH算法原理

BIRCH算法中引入了两个概念：聚类特征和聚类特征树，以下分别介绍。

聚类特征（CF）

CF 是 BIRCH 增量聚类算法的核心，CF 树中得节点都是由 CF 组成，一个 CF 是一个三元组，这个三元组就代表了簇的所有信息。给定 N 个 d 维的数据点 $\{x_1,x_2,…,x_n\}$，CF 定义如下：CF=(N，LS，SS)。其中，N 是子类中节点的数目，LS 是 N 个节点的线性和，SS 是 N 个节点的平方和。

CF 有个特性，即可以求和，具体说明如下：CF1=（n1,LS1,SS1），CF2=（n2,LS2,SS2），则 CF1+CF2=（n1+n2,LS1+LS2,SS1+SS2）。假设簇 C1 中有三个数据点：（2,3），（4,5），（5,6），则 CF1={3，（2+4+5,3+5+6），（2^2+4^2+5^2,3^2+5^2+6^2）}={3，（11,14），（45,70）}，同样的，簇 C2 的 CF2={4，（40,42），（100,101）}，那么，由簇 C1 和簇 C2 合并而来的簇 C3 的聚类特征 CF3 计算如下：CF3={3+4,（11+40,14+42），（45+100,70+101）}={7，（51,56），（145,171）}

另外在介绍两个概念：簇的质心和簇的半径。假如一个簇中包含 n 个数据点：$X_i,i=1,2,3…n$，则质心 $X_0$ 和半径 R 计算公式如下：

$$X_0=\frac{\sum_{i=1}^{n}X_i}{n}$$

$$R=\sqrt{\frac{\sum_{i=1}^{n}(X_i-X_0)^2}{n}}$$

其中，簇半径表示簇中所有点到簇质心的平均距离。CF 中存储的是簇中所有数据点的特性的统计和，所以当我们把一个数据点加入某个簇的时候，那么这个数据点的详细特征，例如属性值，就丢失了，由于这个特征，BIRCH 聚类可以在很大程度上对数据集进行压缩。

聚类特征树（CF tree）

CF tree 的结构类似于一棵 B-树，它有两个参数：内部节点平衡因子 B，叶节点平衡因子 L，簇半径阈值 T。树中每个节点最多包含 B 个孩子节点，记为 $({CF}_i，{CHILD}_i)$，1<=i<=B，${CF}_i$ 是这个节点中的第 i 个聚类特征，${CHILD}_i$ 指向节点的第 i 个孩子节点，对应于这个节点的第 i 个聚类特征。例如，一棵高度为 3，B 为 2，L 为 3 的一棵 CF 树的例子如图所示：

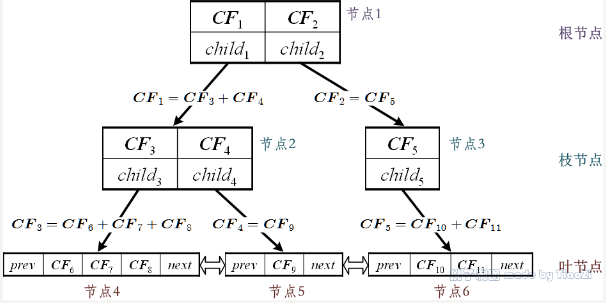
聚类特征树 CFTree 的生成

一棵 CF 树是一个数据集的压缩表示，叶子节点的每一个输入都代表一个簇 C，簇 C 中包含若干个数据点，并且原始数据集中越密集的区域，簇 C 中包含的数据点越多，越稀疏的区域，簇 C 中包含的数据点越少，簇 C 的半径小于等于 T。随着数据点的加入，CF 树被动态的构建，插入过程有点类似于 B-树。加入算法表示如下：

(1) 从根节点开始，自上而下选择最近的孩子节点
(2) 到达叶子节点后，检查最近的元组 CFi 能否吸收此数据点
是，更新 CF 值
否，是否可以添加一个新的元组
是，添加一个新的元组
否则，分裂最远的一对元组，作为种子，按最近距离重新分配其它元组
(3) 更新每个非叶节点的 CF 信息，如果分裂节点，在父节点中插入新的元组，检查分裂，直到 root

下面我们看看怎么生成 CFTree。我们先定义好 CFTree 的参数：即内部节点的最大 CF 数 B，叶子节点的最大 CF 数 L，叶节点每个 CF 的最大样本半径阈值 T。

在最开始的时候，CFTree 是空的，没有任何样本，我们从训练集读入第一个样本点，将它放入一个新的 CF 三元组 A，这个三元组的 N=1，将这个新的 CF 放入根节点，此时的 CFTree 如下图：

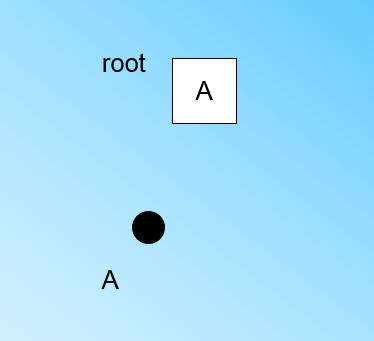
现在我们继续读入第二个样本点，我们发现这个样本点和第一个样本点 A，在半径为 T 的超球体范围内，也就是说，他们属于一个 CF，我们将第二个点也加入 CFA, 此时需要更新 A 的三元组的值。此时 A 的三元组中 N=2。此时的 CFTree 如下图：

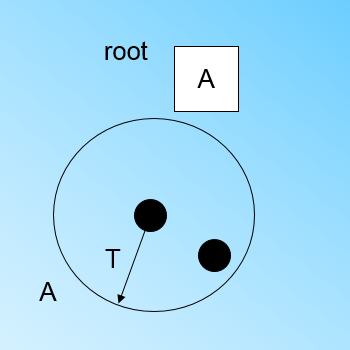
此时来了第三个节点，结果我们发现这个节点不能融入刚才前面的节点形成的超球体内，也就是说，我们需要一个新的 CF 三元组 B，来容纳这个新的值。此时根节点有两个 CF 三元组 A 和 B，此时的 CFTree 如下图：

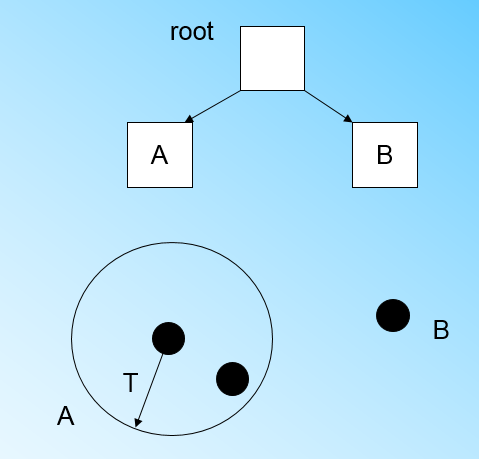
当来到第四个样本点的时候，我们发现和 B 在半径小于 T 的超球体，这样更新后的 CFTree 如下图：

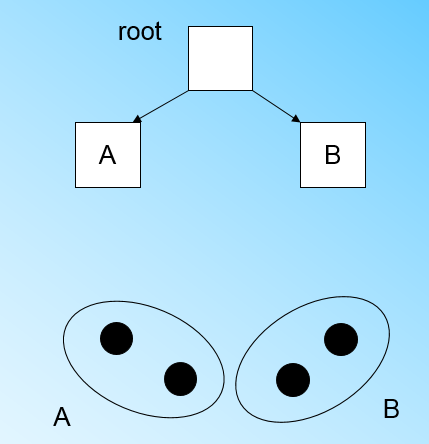
那个什么时候 CFTree 的节点需要分裂呢？假设我们现在的 CFTree 如下图，叶子节点 LN1 有三个 CF，LN2 和 LN3 各有两个 CF。我们的叶子节点的最大 CF 数 L=3。此时一个新的样本点来了，我们发现它离 LN1 节点最近，因此开始判断它是否在 sc1,sc2,sc3 这 3 个 CF 对应的超球体之内，但是很不幸，它不在，因此它需要建立一个新的 CF，即 sc8 来容纳它。问题是我们的 L=3，也就是说 LN1 的 CF 个数已经达到最大值了，不能再创建新的 CF 了，怎么办？此时就要将 LN1 叶子节点一分为二了。

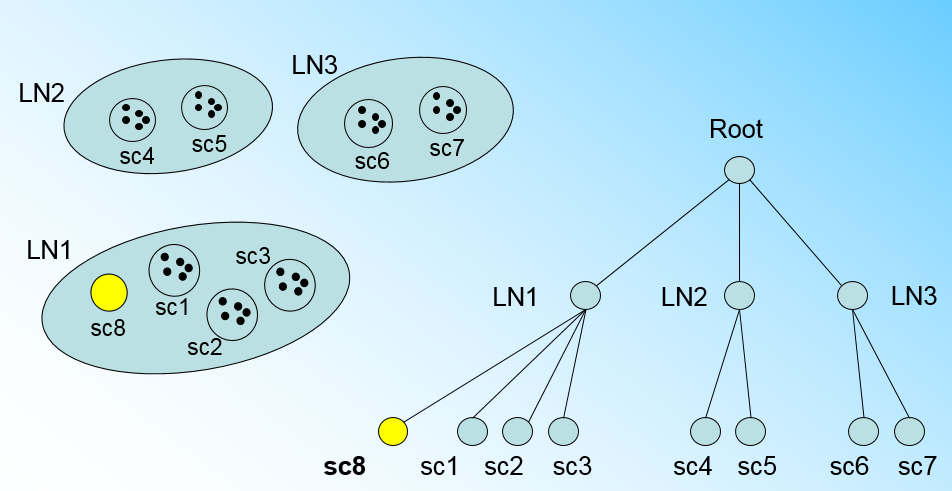
将 LN1 里所有 CF 元组中，找到两个最远的 CF 做这两个新叶子节点的种子 CF，然后将 LN1 节点里所有 CF sc1,sc2,sc3，以及新样本点的新元组 sc8 划分到两个新的叶子节点上。将 LN1 节点划分后的 CFTree 如下图：

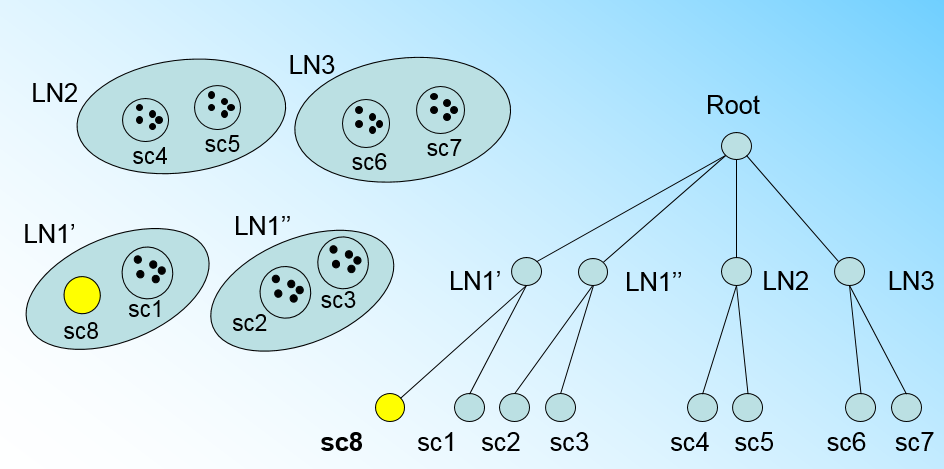如果我们的内部节点的最大CF数 B=3，则此时叶子节点一分为二会导致根节点的最大CF数超了，也就是说，我们的根节点现在也要分裂，分裂的方法和叶子节点分裂一样，分裂后的CFTree如下图：

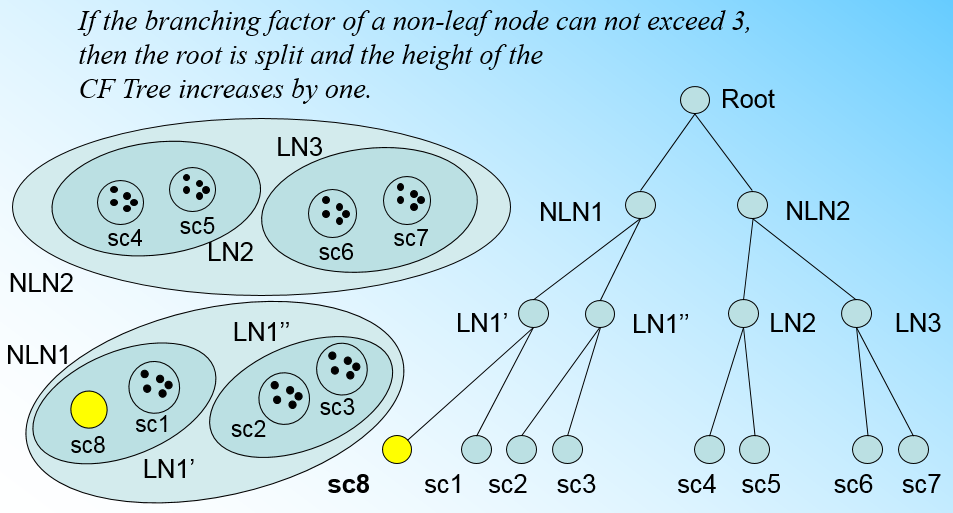
有了上面这一系列的图，相信大家对于CFTree的插入就没有什么问题了，总结下CFTree的插入：

1. 从根节点向下寻找和新样本距离最近的叶子节点和叶子节点里最近的CF节点
2. 如果新样本加入后，这个CF节点对应的超球体半径仍然满足小于阈值 T，则更新路径上所有的CF三元组，插入结束。否则转入3.
3. 如果当前叶子节点的CF节点个数小于阈值 L，则创建一个新的CF节点，放入新样本，将新的CF节点放入这个叶子节点，更新路径上所有的CF三元组，插入结束。否则转入4。

4.将当前叶子节点划分为两个新叶子节点，选择旧叶子节点中所有CF元组里超球体距离最远的两个CF元组，分布作为两个新叶子节点的第一个CF节点。将其他元组和新样本元组按照距离远近原则放入对应的叶子节点。依次向上检查父节点是否也要分裂，如果需要按和叶子节点分裂方式相同。

对于上图所示的CF-树，假设现在添加一个新的簇 $CF_{12}$，这个簇距离 $CF_8$ 最近，但是不满足被吸收的条件（$CF_8$ 和 $CF_{12}$ 之间的距离大于了阈值），加入过程如下：

1. 用 $CF_8$ 跟 $CF_1$ 和 $CF_2$ 比较距离，发现离 $CF_1$ 更近, 找到 $CF_1$ 的子节点 $CF_3$ 和 $CF_4$
2. 同步骤1，找到 $CF_3$ 的子节点，发现为叶子节点4：$\{CF_6, CF_7, CF_8\}$
3. 尝试把 $CF_{12}$ 加入到叶子节点4，此时节点4的数量为4，超过了我们设定的 L 值3，所以现在需要分离节点4，将 $CF_8$ 和 $CF_{12}$ 分到一个新的叶子节点，然后剩下 $CF_6$ 和 $CF_7$
4. 同时在节点2中加入一个新的非叶子节点，此时节点2的数量为3，大于我们设定的 B 值2，进一步拆分节点2为两个新的非叶子节点
5. 同步骤4，知道所有的节点都满足CF-树种 B=2，L=3 的约束
6. 更新所有CF节点对应的特征值，得到如下的新CF-树：

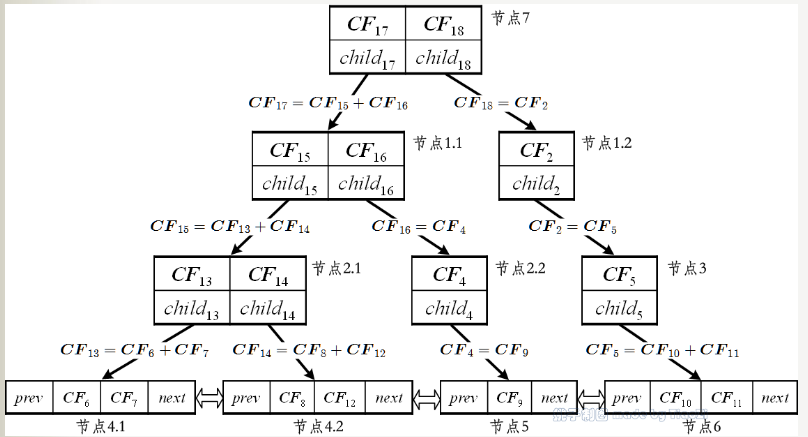
BIRCH算法流程

上面讲了半天的CFTree，终于我们可以步入正题BIRCH算法，其实将所有的训练集样本建立了CFTree，一个基本的BIRCH算法就完成了，对应的输出就是若干个CF节点，每个节点里的样本点就是一个聚类的簇。也就是说BIRCH算法的主要过程，就是建立CFTree的过程。当然，真实的BIRCH算法除了建立CFTree来聚类，其实还有一些可选的算法步骤的，现在我们就来看看BIRCH算法的流程：

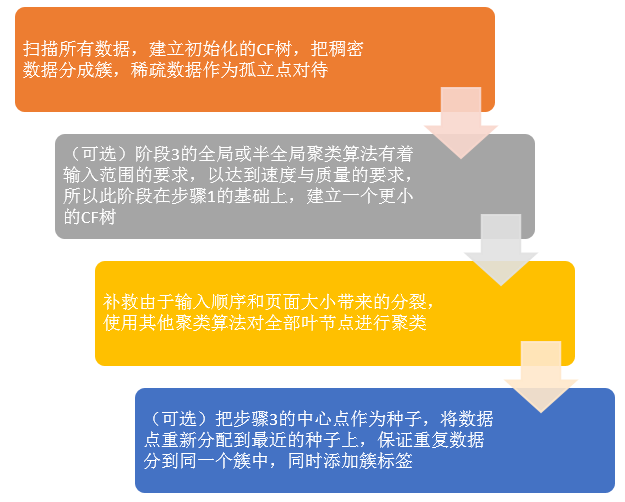
1. 将所有的样本依次读入，在内存中建立一颗CFTree, 建立的方法参考上一节。
2. （可选）将第一步建立的CFTree进行筛选，去除一些异常CF节点，这些节点一般里面的样本点很少。对于一些超球体距离非常近的元组进行合并
3. （可选）利用其它的一些聚类算法比如K-Means对所有的CF元组进行聚类，得到一颗比较好的CFTree. 这一步的主要目的是消除由于样本读入顺序导致的不合理的树结构，以及一些由于节点CF个数限制导致的树结构分裂。
4. （可选）利用第三步生成的CFTree的所有CF节点的质心，作为初始质心点，对所有的样本点按距离远近进行聚类。这样进一步减少了由于CFTree的一些限制导致的聚类不合理的情况。

从上面可以看出，BIRCH算法的关键就是步骤1，也就是CFTree的生成，其他步骤都是为了优化最后的聚类结果。

BIRCH算法的主流程如下：

BIRCH算法小结

BIRCH算法可以不用输入类别数 K 值，这点和 K-Means，MiniBatch K-Means不同。如果不输入 K 值，则最后的CF元组的组数即为最终的 K，否则会按照输入的 K 值对CF元组按距离大小进行合并。一般来说，BIRCH算法适用于样本量较大的情况，这点和 MiniBatch K-Means类似，但是BIRCH适用于类别数比较大的情况，而 MiniBatch K-Means一般用于类别数适中或者较少的时候。BIRCH除了聚类还可以额外做一些异常点检测和数据初步按类别规约的预处理。但是如果数据特征的维度非常大，比如大于20，则BIRCH不太适合，此时 MiniBatch K-Means的表现较好。对于调参，BIRCH要比 K-Means，MiniBatch K-Means复杂，因为它需要对CFTree的几个关键的参数进行调参，这几个参数对CFTree的最终形式影响很大。

BIRCH算法的主要优点有：

• 节省内存。叶子节点放在磁盘分区上，非叶子节点仅仅是存储了一个CF值，外加指向父节点和孩子节点的指针。
• 速度快。合并两个两簇只需要两个类簇的CF元组直接相加即可，计算两个簇的距离只需要用到(N, LS, SS)这三个值。
• 一遍扫描数据库即可建立CFTree。
• 可识别噪声点。建立好CFTree后把那些包含数据点少的MinCluster当作outlier。
• 由于CFTree是高度平衡的，所以在树上进行插入或查找操作很快。

BIRCH算法的主要缺点有：

• 结果依赖于数据点的插入顺序。本属于同一个簇的点可能由于插入顺序相差很远而分到不同的簇中，即使同一个点在不同的时刻被插入，也会被分到不同的簇中。
• 对非球状的簇聚类效果不好。这取决于簇直径和簇间距离的计算方法。
• 对高维数据聚类效果不好。
• 由于每个节点只能包含一定数目的子节点，最后得出来的簇可能和自然簇相差很大。BIRCH适合于需要产生大量的子簇的场景，但在整个过程中算法一旦中断，一切必须从头再来。
• 局部性导致了BIRCH的聚类效果欠佳。当一个新数据点要插入时，它只跟很少一部分簇进行了相似性（通过计算簇间距离）比较，高效率不一定带来好效果。

在scikit-learn中使用BIRCH

在scikit-learn中，BIRCH类实现了基于特征树CFTree的聚类。因此要使用BIRCH来聚类，关键是对CFTree结构参数的处理。在CFTree中，几个关键的参数为内部节点的最大CF数 B，叶子节点的最大CF数 L，叶节点每个CF的最大样本半径阈值 T。这三个参数定了，CFTree的结构也基本确定了，最后的聚类效果也基本确定。可以说BIRCH的调参就是调试 B, L 和 T。至于类别数 K，此时反而是可选的，不输入 K，则BIRCH会对CFTree里各叶子节点CF中样本的情况自己决定类别数 K 值，如果输入 K 值，则BIRCH会CFTree里各叶子节点CF进行合并，直到类别数为 K。

class sklearn.cluster.Birch(*, threshold=0.5, branching_factor=50, n_clusters=3, compute_labels=True, copy=True)

参入参数：

• threshold：即叶节点每个CF的最大样本半径阈值 T，它决定了每个CF里所有样本形成的超球体的半径阈值。一般来说 threshold 越小，则CFTree的建立阶段的规模会越大，即BIRCH算法第一阶段所花的时间和内存会越多。但是选择多大以达到聚类效果则需要通过调参决定。默认值是5.如果样本的方差较大，则一般需要增大这个默认值。

branching_factor：即 CFTree 内部节点的最大 CF 数 B，以及叶子节点的最大 CF 数 L。这里 scikit-learn 对这两个参数进行了统一取值。也就是说，branching_factor 决定了 CFTree 里所有节点的最大 CF 数。默认是 50。如果样本量非常大，比如大于 10 万，则一般需要增大这个默认值。选择多大的 branching_factor 以达到聚类效果则需要通过和 threshold 一起调参决定

• n_clusters：即类别数 K，在 BIRCH 算法是可选的，如果类别数非常多，我们也没有先验知识，则一般输入 None，此时 BIRCH 算法第 4 阶段不会运行。但是如果我们有类别的先验知识，则推荐输入这个可选的类别值。默认是 3，即最终聚为 3 类。
• compute_labels：布尔值，表示是否标示类别输出，默认是 True。一般使用默认值挺好，这样可以看到聚类效果。

实例代码：

from sklearn.datasets import make_blobs
from sklearn.cluster import Birch
import matplotlib.pyplot as plt

# 生成样本点
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels = make_blobs(n_samples=750, centers=centers,
cluster_std=0.4, random_state=0)

clustering = Birch(n_clusters=3).fit(X)
plt.figure(figsize=(10, 8))
plt.scatter(X[:, 0], X[:, 1], c=clustering.labels_, cmap='prism')
plt.show()

参考链接：

• BIRCH 聚类算法原理
• 用 scikit-learn 学习 BIRCH 聚类
• https://scikit-learn.org/stable/modules/generated/sklearn.cluster.Birch.html