超参数调优是机器学习模型开发的核心步骤,直接影响模型性能。scikit-learn 提供多种工具帮助高效优化参数。
GridSearchCV
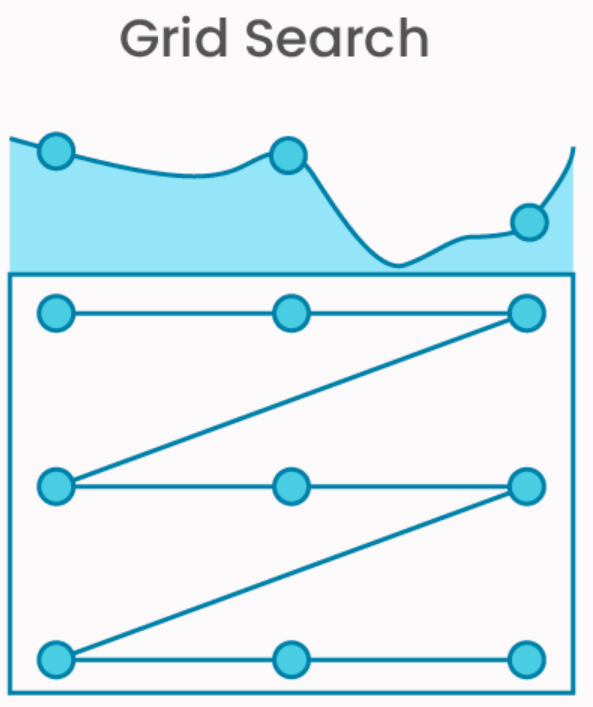
Scikit-Learn 的 GridSearchCV 是一种通过穷举参数组合并交叉验证评估性能的超参数调优工具,适用于参数空间较小且需要全面搜索的场景。
核心原理
- 穷举搜索:遍历用户定义的参数网格(param_grid)中所有可能的参数组合。
- 交叉验证评估:对每个参数组合,使用交叉验证计算模型性能得分(如准确率、F1-score),最终选择得分最高的参数。
关键参数解析
| 参数 | 说明 |
| estimator | 待调优的模型对象(如 SVC(), RandomForestClassifier())。 |
| param_grid | 参数网格(字典或列表),指定待搜索的参数及取值范围(如 {‘C’: [0.1, 1, 10], ‘kernel’: [‘linear’, ‘rbf’]})。 |
| cv | 交叉验证策略(默认为5折),支持整数(指定折数)或交叉验证生成器(如 KFold)。 |
| scoring | 评估指标(如 ‘accuracy’, ‘f1’),默认为模型的默认评分函数。 |
| n_jobs | 并行运行的作业数(-1 表示使用所有CPU核心)。 |
| verbose | 输出详细日志(值越大信息越多,如 verbose=2 显示每个参数组合的得分)。 |
| refit | 是否用最佳参数在完整数据集上重新训练模型(默认为 True,便于后续直接预测)。 |
工作流程
- 生成参数组合:根据param_grid 生成所有可能的参数组合。
- 交叉验证评估:
- 将数据划分为训练集和验证集(cv次)。
- 对每个参数组合训练模型,计算平均验证得分。
- 选择最佳参数:选择平均得分最高的参数组合。
- 重新训练模型(可选):若refit=True,使用最佳参数在整个数据集上训练最终模型。
使用示例
# 步骤1:导入库与数据
from sklearn import datasets
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
# 加载数据集(以鸢尾花数据集为例)
X, y = datasets.load_iris(return_X_y=True)
# 步骤2:定义模型与参数网格
model = SVC()
# 参数网格(需覆盖目标模型的超参数)
param_grid = {
'C': [0.1, 1, 10], # 正则化参数
'kernel': ['linear', 'rbf'], # 核函数类型
'gamma': ['scale', 'auto'] # 核函数系数(仅对rbf生效)
}
# 步骤3:执行网格搜索
grid_search = GridSearchCV(
estimator=model,
param_grid=param_grid,
cv=5, # 5折交叉验证
scoring='accuracy', # 评估指标
n_jobs=-1, # 使用所有CPU核心
verbose=2 # 显示详细日志
)
grid_search.fit(X, y) # 开始搜索
#步骤4:获取最佳参数与模型
print("最佳参数:", grid_search.best_params_) # 输出: {'C': 1, 'gamma': 'scale', 'kernel': 'linear'}
print("最佳模型得分:", grid_search.best_score_) # 输出: 0.98
# 使用最佳模型预测(需refit=True)
best_model = grid_search.best_estimator_
predictions = best_model.predict(X)
# 步骤5:分析所有参数组合结果
import pandas as pd
# 将结果转为DataFrame
results = pd.DataFrame(grid_search.cv_results_)
print(results[['params', 'mean_test_score', 'std_test_score']])
# 输出示例:
# params mean_test_score std_test_score
# 0 {'C': 0.1, 'gamma': 'scale', 'kernel': 'linear'} 0.966667 0.024944
# 1 {'C': 0.1, 'gamma': 'auto', 'kernel': 'linear'} 0.966667 0.024944
# ... ... ...
核心优缺点
| 优点 | 缺点 |
| 确保找到参数网格内的全局最优解。 | 计算成本高(参数组合数随维度指数增长)。 |
| 结果可解释性强,适合小参数空间。 | 不适用于高维参数空间(如超过3个参数)。 |
实用技巧
参数网格设计
- 精简参数范围:优先测试关键参数的对数空间(如C: [0.1, 1, 10])。
- 条件参数:使用列表字典处理依赖参数(如仅当kernel=’rbf’ 时生效的 gamma):
param_grid = [
{'kernel': ['linear'], 'C': [0.1, 1, 10]},
{'kernel': ['rbf'], 'C': [0.1, 1, 10], 'gamma': ['scale', 'auto']}
]
加速计算
- 并行化:设置n_jobs=-1 利用多核CPU。
- 数据采样:大数据集时,可对训练数据进行随机子采样。
验证曲线辅助分析
结合 validation_curve 观察单一参数对模型性能的影响,缩小网格搜索范围:
from sklearn.model_selection import validation_curve
import numpy as np
param_range = np.logspace(-3, 3, 7)
train_scores, test_scores = validation_curve(
SVC(), X, y, param_name='C', param_range=param_range, cv=5
)
总结
- 适用场景:超参数数量少(2-3个)且需要精确调优时。
- 最佳实践:
- 优先用validation_curve 或先验知识缩小参数范围。
- 结合并行计算和交叉验证确保稳定性。
- 避免过大的参数网格(如超过1000种组合)。
通过合理设计参数网格和利用Scikit-Learn的高效实现,GridSearchCV 可显著提升模型性能,尤其适合对模型效果要求严苛的场景。
RandomizedSearchCV
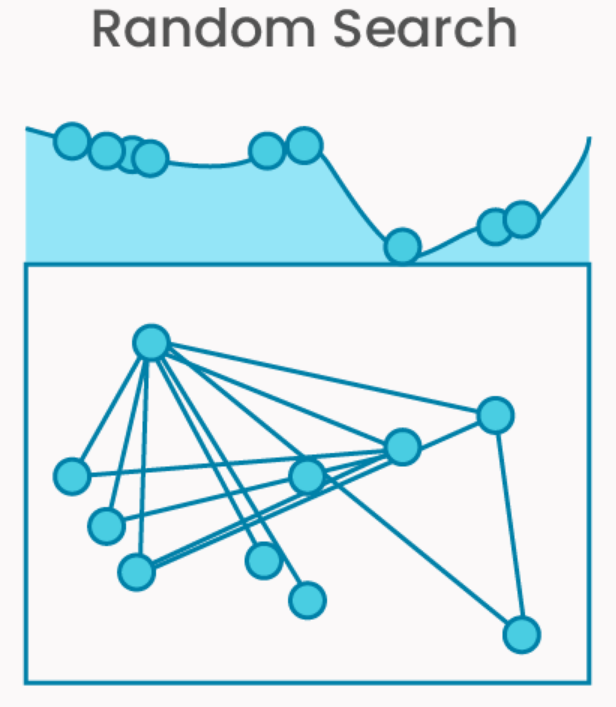
Scikit-Learn 的 RandomizedSearchCV 是一种基于随机采样的超参数调优工具,适用于参数空间较大或计算资源有限的场景。与 GridSearchCV 的穷举搜索不同,它通过随机抽取参数组合并评估性能,以更低的计算成本找到近似最优解。
核心原理
- 随机采样:从用户定义的参数分布中随机抽取n_iter 次参数组合(而非穷举所有可能)。
- 交叉验证评估:对每个采样的参数组合进行交叉验证,计算模型性能得分,最终选择得分最高的参数。
- 核心优势:在牺牲全局最优性的前提下,显著减少计算量,适用于高维参数空间或计算资源受限的场景。
关键参数解析
| 参数 | 说明 |
| estimator | 待调优的模型对象(如 RandomForestClassifier())。 |
| param_distributions | 参数分布字典(值可为分布对象或列表),如 {‘C’: loguniform(0.1, 10), ‘max_depth’: [3, 5, None]}。 |
| n_iter | 随机采样次数(默认10),值越大搜索越全面,但耗时增加。 |
| cv | 交叉验证策略(默认为5折)。 |
| scoring | 评估指标(如 ‘roc_auc’, ‘neg_mean_squared_error’)。 |
| n_jobs | 并行任务数(-1 表示使用所有CPU核心)。 |
| random_state | 随机种子,确保结果可复现。 |
| refit | 是否用最佳参数重新训练模型(默认为 True)。 |
工作流程
- 定义参数分布:为每个超参数指定统计分布(如均匀分布、对数均匀分布)或离散值列表。
- 随机采样:从参数分布中抽取n_iter 个参数组合。
- 交叉验证评估:对每个参数组合训练模型并计算平均验证得分。
- 选择最佳参数:选择得分最高的参数组合,并(可选)重新训练最终模型。
使用示例
# 步骤1:导入库与数据
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import loguniform, randint
# 加载数据集
X, y = load_breast_cancer(return_X_y=True)
# 步骤2:定义模型与参数分布
model = RandomForestClassifier()
# 参数分布(支持连续分布和离散值)
param_dist = {
'n_estimators': randint(50, 200), # 整数均匀分布
'max_depth': [3, 5, None], # 离散值列表
'max_features': ['sqrt', 'log2', None], # 分类分布
'bootstrap': [True, False], # 布尔值
'criterion': ['gini', 'entropy'], # 分类分布
'min_samples_split': randint(2, 10), # 整数均匀分布
'min_samples_leaf': randint(1, 5), # 整数均匀分布
'class_weight': [None, 'balanced'] # 混合类型
}
# 步骤3:执行随机搜索
random_search = RandomizedSearchCV(
estimator=model,
param_distributions=param_dist,
n_iter=50, # 采样50次(远小于所有可能组合数)
cv=5,
scoring='roc_auc',
n_jobs=-1,
random_state=42,
verbose=1
)
random_search.fit(X, y)
# 步骤4:获取最佳结果
print("最佳参数:", random_search.best_params_)
print("最佳AUC得分:", random_search.best_score_)
# 使用最佳模型预测
best_model = random_search.best_estimator_
probabilities = best_model.predict_proba(X)[:, 1]
# 步骤5:分析所有采样结果
import pandas as pd
results = pd.DataFrame(random_search.cv_results_)
results.sort_values('rank_test_score', inplace=True)
print(results[['params', 'mean_test_score', 'std_test_score']].head(10))
参数分布设计技巧
连续参数分布
使用 scipy.stats 中的分布对象(需导入):
from scipy.stats import uniform, loguniform, expon
param_dist = {
'C': loguniform(1e-3, 1e3), # 对数均匀分布(适合尺度敏感参数)
'gamma': expon(scale=0.1), # 指数分布(倾向于小值)
'learning_rate': uniform(0.01, 0.3) # 均匀分布
}
离散参数
直接使用列表定义离散值:
param_dist = {
'kernel': ['linear', 'rbf', 'poly'],
'degree': [2, 3, 4]
}
条件参数
使用字典列表处理参数依赖关系(如某些参数仅在特定条件下生效):
param_dist = [
{'kernel': ['linear'], 'C': loguniform(1e-3, 1e3)},
{'kernel': ['rbf'], 'C': loguniform(1e-3, 1e3), 'gamma': loguniform(1e-4, 1e1)}
]
核心优缺点
| 优点 | 缺点 |
| 计算效率高,适合高维参数空间。 | 可能错过全局最优解(依赖采样次数)。 |
| 支持连续分布,更灵活的参数空间探索。 | 结果方差较大(需多次运行或增大 n_iter)。 |
| 可通过调整 n_iter 平衡效率与效果。 | 需要手动设计参数分布。 |
实用技巧
加速搜索
- 并行计算:设置n_jobs=-1 充分利用多核CPU。
- 减少交叉验证折数:如使用cv=3(需权衡评估稳定性)。
- 数据子采样:对训练数据进行随机采样(适用于大数据集)。
参数分布设计
- 对数尺度参数:对尺度敏感的参数(如学习率、正则化强度)使用loguniform,而非线性均匀分布。
- 先验知识引导:根据文献或初步实验,缩小参数范围。
结果稳定性
- 多次运行:设置不同random_state 多次运行,观察最佳参数的一致性。
- 增大n_iter:在计算资源允许时增加采样次数(如从50增至200)。
与网格搜索结合
- 粗调:先用RandomizedSearchCV 在大范围参数空间中快速筛选出优质区域。
- 精调:在缩小后的参数范围内使用GridSearchCV 进行精细搜索。
对比 GridSearchCV
| 特性 | GridSearchCV | RandomizedSearchCV |
| 搜索策略 | 穷举所有参数组合 | 随机采样参数组合 |
| 计算成本 | 高(指数级增长) | 低(线性增长,由 n_iter 控制) |
| 参数类型 | 仅支持离散值 | 支持连续分布和离散值 |
| 适用场景 | 小参数空间(2-3个参数) | 大参数空间或高维参数 |
| 结果最优性 | 保证找到网格内最优解 | 可能找到近似最优解 |
| 资源利用率 | 低(可能评估大量无效参数) | 高(更可能探索有潜力的区域) |
总结
- 适用场景:
- 超参数数量多(≥4个)或参数范围广。
- 需要快速探索参数空间(如原型开发或初步实验)。
- 参数包含连续值或需非均匀采样(如对数尺度)。
- 最佳实践:
- 优先用连续分布替代离散列表(如loguniform 替代 [0.001, 0.01, 0.1, 1])。
- 设置n_iter 至少为50~100,确保采样覆盖率。
- 结合交叉验证和多次运行验证结果稳定性。
通过合理设计参数分布和利用随机搜索的高效性,RandomizedSearchCV 能够在有限计算资源下显著提升模型性能,是大规模调优任务的实用工具。
HalvingGridSearchCV 和 HalvingRandomSearchCV
Scikit-Learn 的 HalvingGridSearchCV 和 HalvingRandomSearchCV 是基于 Successive Halving(连续减半) 策略的超参数调优工具,旨在通过逐步淘汰低性能参数组合,大幅降低计算成本。这两种方法尤其适合 参数空间较大 或 训练资源有限 的场景。
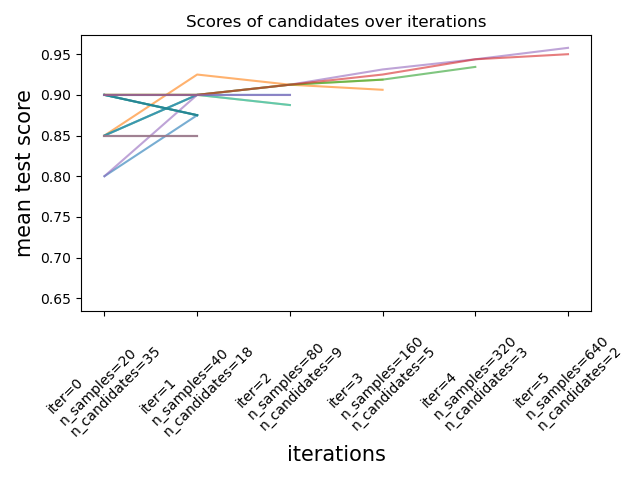
Successive Halving 核心原理
- 核心思想:通过多轮迭代逐步淘汰弱参数组合,集中资源评估优质候选。
- 资源分配:每轮迭代中,为每个候选参数分配更多资源(如更大的训练数据子集或更长的训练时间)。
- 淘汰机制:每轮结束后,仅保留得分最高的部分参数进入下一轮,其余被淘汰。
- 关键参数:
- factor:每轮淘汰比例(如factor=3 表示每轮保留1/3的候选)。
- min_resources:第一轮分配的最小资源量(如训练样本数)。
- max_resources:最大可用资源总量(如总训练样本数)。
示例流程(factor=2, min_resources=100, max_resources=1000):
- 第1轮:100个样本训练所有候选参数 → 淘汰一半。
- 第2轮:200个样本训练剩余参数 → 再淘汰一半。
- 第3轮:400个样本训练剩余参数 → 最终选出最佳参数。
HalvingGridSearchCV
特点
- 基于网格搜索(穷举参数组合),但使用 Successive Halving 策略加速。
- 适用场景:参数组合较少但训练成本高(如深度模型或大数据集)。
关键参数
| 参数 | 说明 |
| param_grid | 与 GridSearchCV 相同的参数网格。 |
| factor | 每轮淘汰比例(默认3)。 |
| aggressive_elimination | 是否强制淘汰至 min_resources 允许的最大轮数(默认False)。 |
| min_resources | 第一轮分配的样本数(默认自动计算)。 |
示例代码
from sklearn.experimental import enable_halving_search_cv # 必须导入
from sklearn.model_selection import HalvingGridSearchCV
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier()
param_grid = {
'max_depth': [5, 10, None],
'min_samples_split': [2, 5, 10],
'criterion': ['gini', 'entropy']
}
halving_grid = HalvingGridSearchCV(
model,
param_grid,
factor=3, # 每轮保留1/3的候选
min_resources=100, # 第一轮用100个样本
cv=5,
scoring='accuracy',
aggressive_elimination=True,
n_jobs=-1
)
halving_grid.fit(X, y)
print("最佳参数:", halving_grid.best_params_)
HalvingRandomSearchCV
特点
- 基于随机搜索(参数采样),结合 Successive Halving 策略提升效率。
- 适用场景:高维参数空间(如超过4个参数)或参数范围广。
关键参数
| 参数 | 说明 |
| param_distributions | 与 RandomizedSearchCV 相同的参数分布。 |
| n_candidates | 初始候选参数数量(默认自动计算,基于 factor 和资源分配)。 |
示例代码
from sklearn.experimental import enable_halving_search_cv
from sklearn.model_selection import HalvingRandomSearchCV
from scipy.stats import loguniform
param_dist = {
'C': loguniform(1e-3, 1e3),
'gamma': loguniform(1e-4, 1e1),
'kernel': ['linear', 'rbf']
}
halving_random = HalvingRandomSearchCV(
SVC(),
param_dist,
factor=2, # 每轮保留1/2的候选
min_resources=200,
cv=3,
random_state=42,
n_jobs=-1
)
halving_random.fit(X, y)
print("最佳参数:", halving_random.best_params_)
核心优势与局限性
优势
| 特性 | 说明 |
| 计算效率 | 早期淘汰弱参数,节省资源用于有潜力的候选。 |
| 资源利用率 | 动态调整资源分配,避免在低质量参数上浪费计算。 |
| 结果质量 | 相比纯随机搜索,更可能找到高性能参数。 |
局限性
| 局限性 | 说明 |
| 参数敏感性 | 依赖 factor 和 min_resources 的合理设置,不当配置可能导致过早淘汰优质参数。 |
| 实现复杂度 | 需理解 Successive Halving 机制,调试成本略高。 |
| Scikit-Learn版本 | 需要 Scikit-Learn ≥ 0.24,且必须显式启用(enable_halving_search_cv)。 |
配置参数技巧
资源分配策略
- min_resources:设置为足够小的值(如总样本的1%),确保早期快速筛选。
- max_resources:通常无需修改(默认使用全部数据)。
- factor:常用2或3,值越小淘汰越激进(适合候选参数多的情况)。
淘汰机制控制
- aggressive_elimination:
- True:强制淘汰至min_resources 允许的最大轮数,可能保留更多候选。
- False:优先用尽max_resources,可能减少总轮数。
交叉验证与稳定性
- cv:减少折数(如cv=3)以加速,但可能降低评估稳定性。
- 多次运行:设置不同随机种子,验证最佳参数的一致性。
与传统搜索方法对比
| 特性 | GridSearchCV | RandomizedSearchCV | Halving系列 |
| 搜索策略 | 穷举网格 | 随机采样 | 分阶段淘汰 + 网格/随机 |
| 资源分配 | 固定资源(全量数据) | 固定资源 | 动态增加资源 |
| 计算成本 | 极高(指数级) | 中等(线性) | 低(淘汰低效参数) |
| 适用场景 | 小参数空间(2-3个参数) | 中高维参数空间 | 中高维参数空间 + 高训练成本 |
| 参数类型 | 离散值 | 离散值 + 连续分布 | 同 Grid/Randomized |
最佳实践总结
- 优先选择 Halving 方法:当参数空间较大或模型训练成本高时,优先使用HalvingGridSearchCV 或 HalvingRandomSearchCV。
- 参数空间设计:
- HalvingGridSearchCV:适合参数数量少但取值多的场景(如C: [0.1, 1, 10, 100])。
- HalvingRandomSearchCV:适合高维参数(如≥4个)或含连续分布的场景。
- 资源分配调优:
- 通过factor 控制淘汰比例,避免过早丢弃优质参数。
- 设置min_resources 为总数据的1%~10%(根据数据规模调整)。
- 结果验证:结合交叉验证和多次运行确保稳定性,必要时用GridSearchCV 微调。
总结
HalvingGridSearchCV 和 HalvingRandomSearchCV 通过动态资源分配和逐步淘汰机制,显著提升了超参数调优的效率,尤其适合以下场景:
- 计算资源有限:需在有限时间内找到较优参数。
- 高训练成本:模型训练耗时(如深度学习)或数据集庞大。
- 参数空间复杂:含多个连续参数或高维离散参数。
实践中建议优先尝试 Halving 方法,再根据结果决定是否需要进一步使用传统网格搜索微调。
验证曲线(validation_curve)
验证曲线是一种用于评估模型在不同超参数取值下的性能变化的工具,通过可视化训练集和验证集的评分,帮助识别过拟合或欠拟合,并确定参数的最优范围。
核心作用
- 诊断模型表现:分析模型对特定超参数的敏感度。
- 指导调参:确定参数的最佳取值范围,避免盲目搜索。
- 平衡偏差与方差:识别过拟合(高方差)或欠拟合(高偏差)。
与学习曲线(Learning Curve)的区别
- 学习曲线:展示模型在不同训练数据量 下的表现(横轴为样本量)。
- 验证曲线:展示模型在不同超参数值 下的表现(横轴为参数值)。
Scikit-Learn 的 validation_curve 函数
函数签名
from sklearn.model_selection import validation_curve
train_scores, test_scores = validation_curve(
estimator, # 模型对象(如SVC())
X, y, # 训练数据
param_name, # 要研究的参数名(如'C')
param_range, # 参数取值范围(如[0.1, 1, 10])
cv=None, # 交叉验证策略
scoring=None, # 评估指标(如'accuracy')
n_jobs=None, # 并行任务数
verbose=0 # 日志详细程度
)
输出结果
- train_scores:每个参数值在训练集上的得分(形状为(n_params, n_cv_folds))。
- test_scores:每个参数值在验证集上的得分(形状同上)。
使用步骤与示例
# 步骤1:导入库与数据
from sklearn.datasets import load_iris
from sklearn.svm import SVC
from sklearn.model_selection import validation_curve
import numpy as np
import matplotlib.pyplot as plt
# 加载数据集
X, y = load_iris(return_X_y=True)
# 步骤2:定义模型与参数范围
model = SVC(kernel='linear', random_state=42)
param_range = np.logspace(-3, 3, 7) # 参数范围:0.001, 0.01, 0.1, 1, 10, 100, 1000
param_name = 'C' # 研究正则化参数C的影响
# 步骤3:计算验证曲线
train_scores, test_scores = validation_curve(
estimator=model,
X=X,
y=y,
param_name=param_name,
param_range=param_range,
cv=5, # 5折交叉验证
scoring='accuracy',
n_jobs=-1
)
# 步骤4:计算均值和标准差
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)
# 步骤5:绘制验证曲线
plt.figure(figsize=(10, 6))
plt.title("Validation Curve with SVM (C parameter)")
plt.xlabel(r"$C$ (Regularization Strength)")
plt.ylabel("Accuracy")
plt.ylim(0.8, 1.02)
plt.semilogx(param_range, train_mean, 'o-', color='r', label='Training Score')
plt.fill_between(param_range, train_mean - train_std, train_mean + train_std, alpha=0.1, color='r')
plt.semilogx(param_range, test_mean, 'o-', color='g', label='Cross-Validation Score')
plt.fill_between(param_range, test_mean - test_std, test_mean + test_std, alpha=0.1, color='g')
plt.axvline(x=1, color='blue', linestyle='--', label='Optimal C (C=1)')
plt.legend(loc='best')
plt.grid(True)
plt.show()
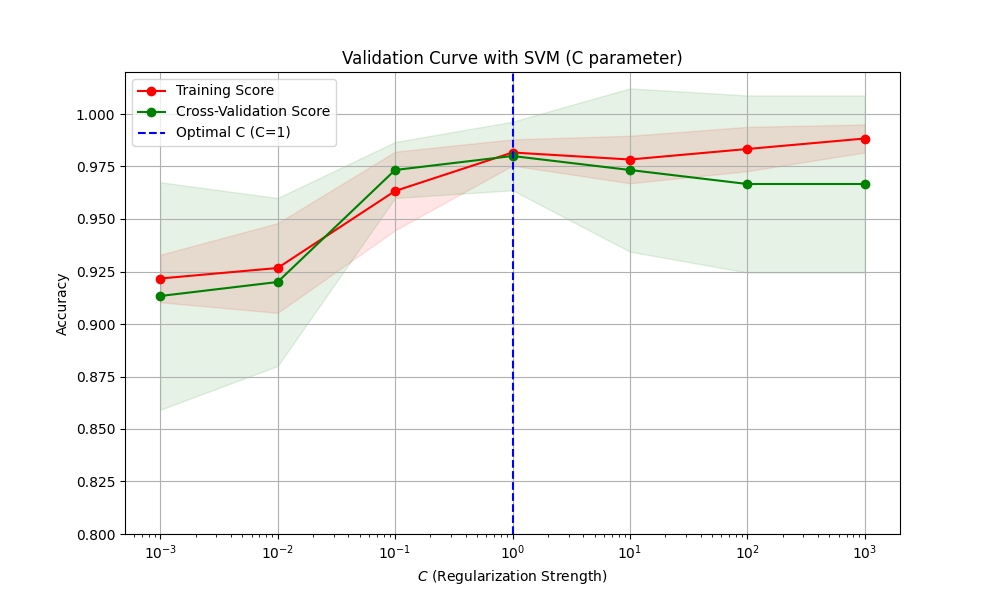
输出图形解析
- 横轴:参数值(对数尺度)。
- 纵轴:模型准确率。
- 红色曲线:训练集得分(反映模型拟合能力)。
- 绿色曲线:验证集得分(反映模型泛化能力)。
- 阴影区域:交叉验证的标准差(稳定性指标)。
验证曲线分析指南
过拟合与欠拟合诊断
| 现象 | 结论 | 解决策略 |
| 训练得分高,验证得分低 | 过拟合(高方差) | 减小模型复杂度(如降低多项式次数、增大正则化强度) |
| 训练得分和验证得分均低 | 欠拟合(高偏差) | 增加模型复杂度(如增加特征、减小正则化强度) |
| 训练得分和验证得分接近且高 | 模型拟合良好 | 无需调整 |
示例分析
- C值过小(如001):强正则化导致欠拟合(训练和验证得分均低)。
- C值过大(如1000):弱正则化导致过拟合(训练得分高,验证得分下降)。
- 最佳C值(如1):训练与验证得分接近且最高(泛化性能最优)。
关键注意事项
- 参数范围选择
- 对数尺度:适用于跨度大的参数(如C、learning_rate),使用logspace生成等比数列。
- 离散值:对分类参数(如max_depth),直接指定候选值列表。
- 交叉验证稳定性
- 增加折数:使用更大的cv值(如10折)减少方差,但计算成本增加。
- 重复交叉验证:使用RepeatedKFold提高结果可靠性。
- 多参数分析
- 单一参数:validation_curve一次仅分析一个参数,多参数需分别绘制。
- 网格搜索辅助:结合GridSearchCV筛选关键参数后再细化分析。
高级技巧
自定义评分函数
支持使用自定义评分函数(需符合Scikit-Learn评分接口):
from sklearn.metrics import make_scorer
def custom_scorer(y_true, y_pred):
return np.sum(y_true == y_pred) / len(y_true)
scorer = make_scorer(custom_scorer)
train_scores, test_scores = validation_curve(
estimator=model,
scoring=scorer,
# 其他参数...
)
多子图对比
同时分析多个参数的影响:
fig, axes = plt.subplots(1, 2, figsize=(15, 5)) # 参数1:C plot_validation_curve(axes[0], param_range_C, train_scores_C, test_scores_C, 'C') # 参数2:gamma plot_validation_curve(axes[1], param_range_gamma, train_scores_gamma, test_scores_gamma, 'gamma') plt.tight_layout() plt.show()
与学习曲线结合
综合分析模型对数据量和参数的敏感度:
from sklearn.model_selection import learning_curve
# 生成学习曲线
train_sizes, train_scores_lc, test_scores_lc = learning_curve(
estimator=model,
X=X,
y=y,
cv=5,
train_sizes=np.linspace(0.1, 1.0, 5)
)
# 绘制学习曲线与验证曲线对比
总结
- 核心价值:快速定位超参数的合理范围,减少调参盲目性。
- 适用阶段:模型开发中期,用于参数敏感性分析和初步调优。
- 最佳实践:
- 优先分析对模型性能影响最大的参数。
- 结合网格搜索或随机搜索进行最终优化。
- 多次运行确保结果稳定性。
ParameterGrid / ParameterSampler
Scikit-Learn 的 ParameterGrid 和 ParameterSampler 是用于生成超参数组合的工具类,分别服务于 网格搜索 和 随机搜索。它们不直接训练模型,而是提供参数组合的生成器,适用于需要自定义超参数遍历逻辑的场景(如手动交叉验证、集成到自定义训练流程等)。
| 工具 | 核心功能 | 适用场景 |
| ParameterGrid | 生成参数网格中所有可能的组合(穷举)。 | 参数空间小,需精确遍历。 |
| ParameterSampler | 从参数分布中随机采样指定数量的组合(支持连续分布)。 | 参数空间大,需高效探索。 |
ParameterGrid 详解
功能:生成所有超参数组合的笛卡尔积,即穷举所有可能的参数组合。每个组合为一个字典,键为参数名,值为对应参数值。
参数配置
- param_grid:参数网格定义,可以是以下两种形式:
- 字典列表(处理条件参数,如某些参数仅在特定条件下有效):
param_grid = [
{'kernel': ['linear'], 'C': [1, 10]},
{'kernel': ['rbf'], 'C': [1, 10], 'gamma': [0.1, 1]}
]
- 字典(简单参数组合):
param_grid = {'C': [0.1, 1, 10], 'kernel': ['linear', 'rbf']}
使用示例
from sklearn.model_selection import ParameterGrid
# 定义参数网格
param_grid = {
'C': [0.1, 1, 10],
'kernel': ['linear', 'rbf'],
'gamma': ['scale', 'auto']
}
# 生成参数组合
grid = ParameterGrid(param_grid)
# 遍历所有参数组合
for params in grid:
print(params)
输出
{'C': 0.1, 'kernel': 'linear', 'gamma': 'scale'}
{'C': 0.1, 'kernel': 'linear', 'gamma': 'auto'}
{'C': 0.1, 'kernel': 'rbf', 'gamma': 'scale'}
...
{'C': 10, 'kernel': 'rbf', 'gamma': 'auto'}
关键特性
- 确定性遍历:生成的参数顺序固定,适合可复现实验。
- 组合数计算:总组合数为各参数取值数量的乘积(如示例中3*2*2=12 种组合)。
- 内存消耗:参数空间大时可能占用较多内存(需生成所有组合)。
ParameterSampler 详解
功能:从参数分布中随机抽取指定数量的参数组合,支持 离散列表 和 连续概率分布(如 scipy.stats 中的分布对象)。
参数配置
- param_distributions:参数分布定义,支持:
- 离散值列表:从列表中无放回抽样。
- 分布对象:如uniform(0, 1),每次采样生成一个随机值。
- n_iter:抽取的样本数(参数组合数)。
- random_state:随机种子,确保结果可复现。
- allow_deprecated:是否允许旧版行为(默认为False)。
使用示例
from sklearn.model_selection import ParameterSampler
from scipy.stats import uniform, randint
# 定义参数分布
param_dist = {
'C': uniform(0.1, 10), # 均匀分布
'kernel': ['linear', 'rbf'], # 离散列表
'gamma': [0.1, 1, 'scale'], # 离散列表
'max_iter': randint(50, 200) # 整数均匀分布
}
# 生成参数组合
sampler = ParameterSampler(
param_distributions=param_dist,
n_iter=5,
random_state=42
)
# 遍历抽样结果
for params in sampler:
print(params)
输出
{'C': 3.745..., 'kernel': 'rbf', 'gamma': 0.1, 'max_iter': 71}
{'C': 9.507..., 'kernel': 'linear', 'gamma': 'scale', 'max_iter': 118}
{'C': 7.319..., 'kernel': 'rbf', 'gamma': 1, 'max_iter': 142}
{'C': 1.438..., 'kernel': 'rbf', 'gamma': 0.1, 'max_iter': 98}
{'C': 9.772..., 'kernel': 'linear', 'gamma': 1, 'max_iter': 168}
关键特性
- 灵活抽样:支持连续分布和离散值混合采样。
- 内存高效:按需生成参数组合,不预先生成所有组合。
- 重复控制:若离散列表元素不足n_iter 且 replace=False,会抛出错误(需设置 replace=True 允许重复)。
高级用法与技巧
条件参数处理
通过字典列表定义互斥的参数组:
param_grid = [
{'kernel': ['linear'], 'C': [1, 10]},
{'kernel': ['rbf'], 'C': [1, 10], 'gamma': [0.1, 1]}
]
自定义分布扩展
使用 scipy.stats 中的任意分布(如正态分布、指数分布):
from scipy.stats import expon
param_dist = {
'learning_rate': expon(scale=0.1), # 指数分布
'batch_size': [32, 64, 128]
}
与自定义训练流程集成
手动遍历参数组合并评估模型:
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
for params in ParameterSampler(param_dist, n_iter=10):
model = SVC(**params).fit(X_train, y_train)
score = accuracy_score(y_test, model.predict(X_test))
print(f"Params: {params}, Score: {score:.4f}")
对比总结
| 特性 | ParameterGrid | ParameterSampler |
| 搜索策略 | 穷举所有组合 | 随机采样指定数量组合 |
| 参数类型 | 仅限离散值列表 | 支持离散列表和连续分布 |
| 组合数 | 指数增长(易爆炸) | 线性增长(由 n_iter 控制) |
| 内存占用 | 高(预生成所有组合) | 低(按需生成) |
| 适用场景 | 参数空间小(如 ≤1000 组合) | 参数空间大或含连续参数 |
实战建议
- 小空间精确搜索:参数组合数 ≤ 1000 时优先用ParameterGrid。
- 大空间高效探索:参数组合数 > 1000 或含连续参数时用ParameterSampler。
- 混合策略:先用ParameterSampler 粗调,再用 ParameterGrid 在优质区域精调。
- 可复现性:为ParameterSampler 设置 random_state 确保结果一致。
- 分布选择:对尺度敏感的参数(如学习率)使用对数均匀分布(loguniform)。
性能优化
- 并行化:使用Parallel 并行评估不同参数组合。
- 提前停止:在自定义训练循环中集成早停机制(如验证损失不再下降时终止训练)。
- 资源控制:限制每个参数组合的训练资源(如迭代次数、数据子集)。
通过合理选择 ParameterGrid 或 ParameterSampler,开发者可以灵活控制超参数搜索的广度和深度,平衡计算成本与模型性能。