图形检验是统计分析中使用图形表示来评估数据的性质或模型拟合优度的一种方法。其中,Q-Q图(Quantile-Quantile Plot)是一种特别常见的图形检验工具,用于比较两个概率分布的形状,尤其是用于检验数据集是否服从某一理论分布,如正态分布、指数分布等。
什么是Q-Q图?
Q-Q图,全称为Quantile-Quantile Plot,是一种用于比较两个概率分布的图形工具,通过这种图可以直观地评估数据集是否服从某一理论分布,或者比较两个数据集的分布特征是否相似。
在Q-Q图中,一个数据集的分位数(quantiles)会与另一个数据集的分位数进行比较。通常,其中一个数据集是样本数据,而另一个是理论分布,如正态分布、指数分布等。如果两个分布相似,则Q-Q图上的点将近似分布在一条直线上。
具体步骤如下:
- 计算两个数据集的分位数。
- 将其中一个分布的分位数(通常是样本数据)绘制在水平轴上。
- 将另一个分布的分位数(通常是理论分布)绘制在垂直轴上。
- 将每一对分位数用点表示在图上。
- 分析点的分布情况:
- 如果点近似一条直线,表明两个数据集分布相似。
- 如果点偏离直线,表明分布之间有差异。
Q-Q图是统计分析中重要的工具之一,其在假设检验和模型诊断中经常用到,例如检验数据是否符合正态分布。
Q-Q图的解读
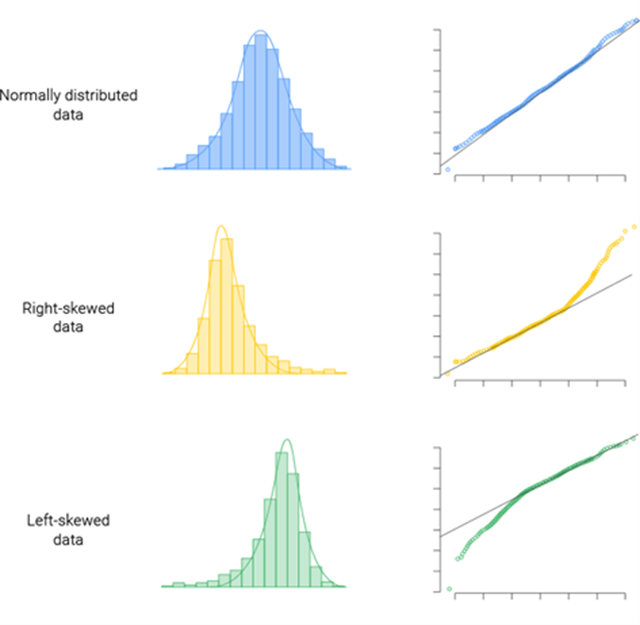
- 线性关系:如果样本数据点在Q-Q图上近似落在一条直线上,这意味着样本数据与理论分布有相同的形状。
- 分布偏态:如果样本数据点在Q-Q图上呈现非线性模式,比如曲线向上或向下弯曲,则表明样本数据与理论分布在偏度上存在差异。
- 分布尾部重度:Q-Q图上的点如在尾部区域偏离直线,可能表示样本分布的尾部比理论分布更重(长尾)或更轻(短尾)。
Q-Q图的应用
Q-Q图的应用场景:
- 正态性检验:最常见的应用是检验数据是否服从正态分布。这在许多统计测试中是一个重要的前提条件。
- 比较两个样本:使用Q-Q图可以比较两个样本集是否来自同一分布。
- 评估模型拟合:在回归分析等统计建模中,Q-Q图可以用来评估残差是否服从某一理论分布,从而判断模型的适用性。
Q-Q图是一种强有力的图形工具,可以直观地展示样本数据与特定理论分布之间的相似性和差异性。然而,需要注意的是,Q-Q图提供的是视觉上的证据,它可以作为正态性或分布性检验的补充工具,但通常不应单独用作正式的统计检验。
使用Q-Q图判断数据是否满足正态分布
使用Q-Q图来检验数据是否符合正态分布的步骤如下:
- 排序:首先将样本数据从小到大排序。
- 计算理论分位数:接着计算标准正态分布(均值为0,标准差为1)的分位数。这通常是通过选择与样本数据相匹配的分位数完成的。例如,如果样本数据中有n个观测值,那么标准正态分布的第k个分位数对应的概率为(k-0.5)/n。
- 计算样本分位数:对于样本数据中的每个排序后的观测值,找到其在样本分布中的相对位置,这通常是通过使用相同的(k-0.5)/n公式来找到的。
- 绘制Q-Q图:在Q-Q图中,横轴(x轴)代表理论分位数,即正态分布的分位数;纵轴(y轴)代表样本分位数。这样,每个样本观测值都会在图中对应一个点。
- 分析Q-Q图:
- 如果样本数据确实符合正态分布,那么Q-Q图上的点将大致落在一条直线上,该直线通过原点,斜率等于样本数据的标准差。
- 如果样本数据的中间部分符合正态分布,但两端偏离(称为“重尾”或“轻尾”现象),则中间的点将近似在直线上,但两端的点会偏离这条直线。
- 如果样本数据不是对称分布,那么点将会形成曲线,而不是直线。
结论:通过以上分析,我们可以大致判断样本数据是否接近正态分布。需要注意的是,这种方法是主观的,因为它依赖于对图形的视觉检查。如果需要更精确的结论,可以使用正态性检验的统计方法,如Kolmogorov-Smirnov检验、Shapiro-Wilk检验等。
要使用Python和Q-Q图检验Pandas DataFrame中某一列的数据是否符合正态分布,你可以使用scipy.stats中的probplot函数,以及matplotlib库来绘制图形。下面是一个基本的步骤和示例代码:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# 假设你已经有了一个Pandas DataFrame,我们将其命名为df,
# 现在我们要检验其中名为"target_column"的列是否符合正态分布
# 创建一个示例DataFrame
data = {'target_column': np.random.normal(loc=0, scale=1, size=100)} # 正态分布样本
df = pd.DataFrame(data)
# 使用scipy的probplot函数计算Q-Q图的值
(stats.probplot(df['target_column'], dist="norm", plot=plt))
# 设置图表标题和轴的标签
plt.title('Q-Q Plot')
plt.xlabel('Theoretical Quantiles')
plt.ylabel('Sample Quantiles')
# 显示Q-Q图
plt.show()
上述代码中,np.random.normal函数生成了一个正态分布的样本数据集,我们以这个数据集为例来创建一个DataFrame。在实际应用中,你应替换为你自己的DataFrame及相应的列名。
stats.probplot函数将计算样本数据的分位数,并与正态分布的理论分位数进行比较。如果target_column列的数据近似正态分布,Q-Q图上的点应该接近参考线。如果点显著偏离这条直线,则可能意味着数据不是正态分布的。
使用Q-Q图判断数据是否满足指数分布
要使用Q-Q图判断数据是否符合指数分布,你需要将样本分位数与指数分布的理论分位数进行比较。下面是使用Python创建指数分布Q-Q图的详细步骤,包括使用scipy.stats中的probplot函数和matplotlib进行绘图:
- 收集数据:获取你要检验的样本数据。
- 排序样本数据:将样本数据按从小到大的顺序排序。
- 计算理论分位数:使用指数分布的累积分布函数(CDF)的逆函数(也称为分位函数)计算理论分位数。
- 绘制Q-Q图:在图中,横轴(x轴)表示理论分布的分位数,纵轴(y轴)表示样本数据的分位数。
- 分析Q-Q图:如果样本数据符合指数分布,则Q-Q图上的点应该近似地落在一条直线上。如果点显著偏离这条直线,则数据可能不符合指数分布。
下面是实现上述步骤的Python代码示例:
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# 假设data是含有样本数据的numpy数组
# 例如:data = np.random.exponential(scale=1.0, size=100) # 这里是随机生成的样本数据
data = np.random.exponential(scale=1.0, size=100) # 示例数据
# 使用scipy的probplot函数,指定dist="expon"来检验指数分布
fig, ax = plt.subplots(figsize=(6, 6))
stats.probplot(data, dist="expon", plot=ax)
# 添加图表标题和轴标签
ax.set_title('Exponential Q-Q plot')
ax.set_xlabel('Theoretical Quantiles')
ax.set_ylabel('Sample Quantiles')
# 显示Q-Q图
plt.show()
在这个示例中,np.random.exponential函数用于随机生成符合指数分布的样本数据。在实际应用中,你应该用你自己的样本数据替换这个数组。stats.probplot函数在这里指定了dist=”expon”参数,以适应指数分布的检验。
分析Q-Q图时,如果样本数据的点大体上落在一条直线上,这表明样本数据可能遵循指数分布。如果点显著偏离直线,则数据可能不是指数分布的。在实际操作中,应结合其他统计检验和图形分析来综合评估数据的分布情况。
使用Q-Q图判断数据分布是否相等
使用Q-Q图(Quantile-Quantile图)来判断两份数据的分布是否相同的过程,涉及将一个数据集的分位数与另一个数据集的分位数进行比较。如果两个数据集来自相同的分布,那么这些点将基本上落在一条45度角的直线上,这条直线称为等分位数线(line of equality)。
下面是判断两份数据分布是否相同的步骤:
- 排序:将两组数据分别按照从小到大的顺序排序。
- 计算分位数:如果两个数据集大小相同,直接比较相同序号位置的值;如果大小不同,比较的是两个数据集的相对分位数。例如,对于第一个数据集的第25个百分位,你需要找到第二个数据集的相同百分位数值。
- 绘制Q-Q图:在Q-Q图中,通常将第一个数据集的分位数作为x轴,将第二个数据集的分位数作为y轴。将每一对分位数用点表示在图上。
- 分析Q-Q图:查看点是否落在等分位数线附近。如果是,两份数据的分布很可能相同;如果点显著偏离这条直线,那么两份数据的分布有显著的不同。
以下是使用Python进行这一过程的示例代码:
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# 假设data1和data2为需要比较的两组数据
data1 = np.random.normal(0, 1, 100) # 第一组数据,正态分布
data2 = np.random.normal(0, 1, 100) # 第二组数据,正态分布,可以修改为其他分布进行测试
# 计算两组数据的分位数
quantiles1 = np.percentile(data1, np.linspace(0, 100, len(data1)))
quantiles2 = np.percentile(data2, np.linspace(0, 100, len(data2)))
# 绘制Q-Q图
plt.scatter(quantiles1, quantiles2)
plt.plot([min(quantiles1), max(quantiles1)], [min(quantiles2), max(quantiles2)], 'r') # 绘制等分位数线
# 增加标题和轴标签
plt.title('Q-Q Plot for Two Datasets')
plt.xlabel('Quantiles of First Data Set')
plt.ylabel('Quantiles of Second Data Set')
# 显示图表
plt.show()
在这个示例中,我们假设data1和data2是来自正态分布的两组数据。我们使用np.percentile函数来计算数据集的百分位数。这些分位数随后被用于绘制Q-Q图。
分析Q-Q图时,如果点基本上落在红色等分位数线上,说明两个数据集的分布相似。如果它们偏离这条直线,说明分布可能存在差异。这种方法特别适用于比较两个数据集的形状、尾部行为和对称性是否相似。



