很多内容网站都会根据用户的交互信息等对内容进行排序。这里整理了一些比较知名的内容网站的排序规则,每个网站都有不同,在此过程中,我们不仅仅要了解其排序规则(公式),更多的期望了解公式背后的逻辑。
HackerNews
HackerNews是一家关于计算机黑客和创业公司的社会化新闻网站,由Paul Graham的创业孵化器Y Combinator创建。与其它社会化新闻网站不同的是HackerNews没有踩或反对一条提交新闻的选项(不过评论还是可以被有足够Karma的用户投反对票,或是投支持票);只可以赞或是完全不投票。简而言之,HackerNews允许提交任何可以被理解为”任何满足人们求知欲”的新闻。
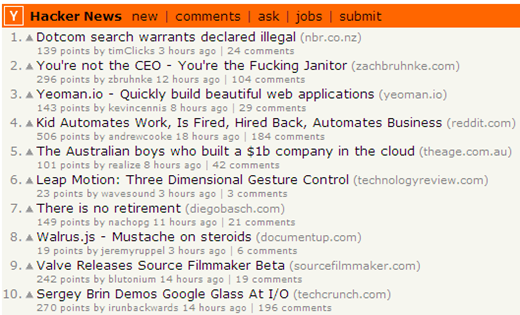
以上为HackerNews的界面截图,如果你是该产品的负责人,你会如何进行排序?哪些维度可以进行排序?
从上面截图中我们考虑的因素主要有:
- 点赞数(每个新闻标题前面有一个向上的三角形,如果你觉得这个内容很好,就点击一下,投上一票)
- 距离发布的时间
- 评论量
最简单的方式是只考虑点赞数,这样点赞数越多的文章的会排在最前面。但是会导致整个站点信息的新颖度不高。即历史的文章由于展示的时间较长点赞数相对会更高。所以需要将时间因素也考虑在内。由于点赞量与评论量存在一定的相关性,且评论量大也有可能是由于内容有较大争议而非热门导致的,所以我们先将影响因素限制在:
- 点赞数:相同发帖时间,投票数越高,分值越高
- 距离发布时间:相同投票数,距离发帖时间越近,分值越高
我们将点赞数设为,发帖时间设为t,则排序分值可以是:
$$score=\frac{P}{t}$$
即分值与点赞数存在正相关,与距离发布时间存在负相关。画出的分值图形如下:
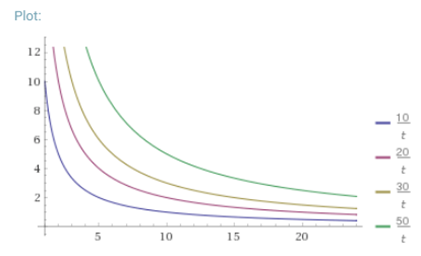
而HackerNews真实采用的公式如下:
$$score=\frac{P-1}{(t+2)^{1.5}}$$
画出的图形如下:
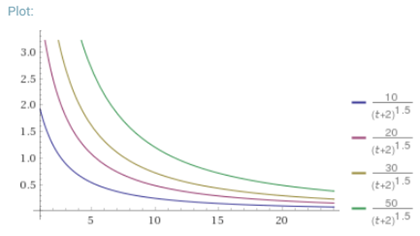
备注:HackerNews采用公式$score=\frac{P-1}{(t+2)^{1.5}}$做为排行依据(HackerNews使用Paul Graham开发的Arc语言编写,源码可以从arclanguage.org下载),其中P是投票数量,t是发表以来的时间,小时计。后来AMIX.DK给出公式$score=\frac{P-1}{(t+2)^{G}}$推广了上面的公式,HackerNews的公式变成了一个特例,其在G=1.5时的应用。历史上HackerNews有用G=1.8。
接下来我们对公式进行分析:
得票数P
在其他条件不变的情况下,得票越多,排名越高。从下图可以看到,有三个同时发表的帖子,得票分别为200票、60票和30票(减1后为199、59和29),分别以黄色、紫色和蓝色表示。在任一个时间点上,都是黄色曲线在最上方,蓝色曲线在最下方。
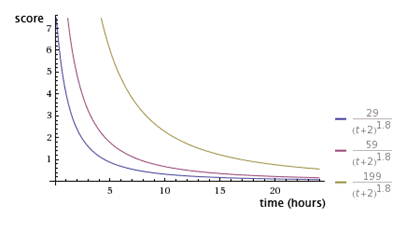
为什么是P-1?网络上的一种解释是,很多文章作者在提交的时候会给自己投上一票。其实更重要的原因是文章发布初期的投票数对排名影响非常的,仅仅是自己给自己投的一票,也占非常大的作用。
假设P不去减去1,一个作者发布完就给自己投票,那么文章的得分为1/(0+2)^1.5=0.3535。假设另外一篇文章发布了8小时,那么需要多少的投票呢?x/(8+2)^1.5>0.3535,即X>11.17即一天前的帖子要有12票才能超过新提交的文章,这显然不合理。
投票数具体应该减去多少,可能需要考虑刷数据的问题,根据网络环境去设置很可能更合理,比如去除同一IP用户的操作等。
另外想要调整得票数的影响权重,可以采用的方式是在得票数上买一个指数。例如你不期望”高投票文章”与”低投票文章差距过大,可以在得票数上加一个小于1的指数,比如(P-1)^0.8。
距离发帖时间t
在其他条件不变的情况下,越是新发表的帖子,排名越高。或者说,一个帖子的排名,会随着时间不断下降。从上图可知,经过24小时之后,所有帖子的得分基本上都小于1,这意味着它们都将跌到排行榜的末尾,保证了排名前列的都将是较新的内容。
公式中为什么要使用t+2?我们先来看下图:
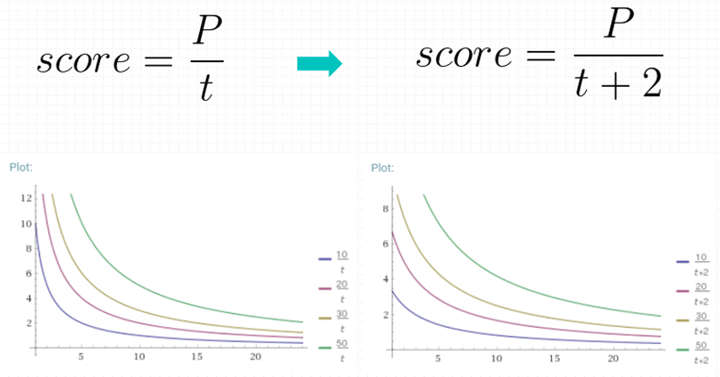
在时间上+2,核心是为了分值曲线向左移,让最开始几个小时过大的下降趋势被舍弃。
重力因子G
它的数值大小决定了排名随时间下降的速度。从下图可以看到,三根曲线的其他参数都一样,G的值分别为1.5、1.8和2.0。G值越大,曲线越陡峭,排名下降得越快。
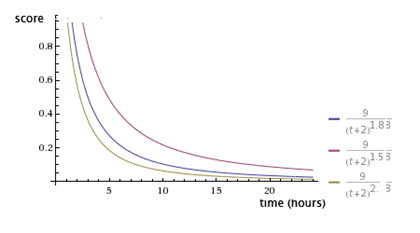
毫无疑问,G这个数字既非时间,也非评价,其实它的主要目的是控制更新频率。G的值越大,score的衰减速度越快,排行的更新越频繁。所以,确定G值需要观察系统内部投票数在时间上的分布,然后根据需要的更新频次确定G的合理取值。越火爆、用户互动越频繁的社区,为了保证排行的稳定性(不要频繁大量的刷新),G值趋向于比较低。这就是为什么HackerNews从一开始的1.8修改成1.5,过段时间可能就变成1.2了。
应用思考
电商网站的热门排序能否使用HackNews的排序规则?答案是不太适合,主要原因的HackerNews是类似新闻类的网站,用户对于信息的更新频率要求比较高。而电商率的网站更多的看中近期或一段时间的热度。两者还是有些差别。
在电商网站上我先前尝试过的公式为:
$$score=\sum(orderCount*\alpha^t)$$
这里主要实现逻辑是取一定范围内的订单,比如30天。计算商品每天的销售量。再在销售量根据距离的天数t进行衰减。其中$\alpha$为0-1之间的衰减系数。
当α=1时,即为最为简单的仅统计浏览量或者订单量的数据,整个公式中最不好确定的是α的取值。我通常使用假设的方式,最后通过不同假设计算出来的结果进行人工的选择。
- 1周后的权重降为5,则$\alpha$^7=0.5,$\alpha$≈0.905724
- 2周后的权重降为5,则$\alpha$^14=0.5,$\alpha$≈0.951695
- 3周后的权重降为5,则$\alpha$^21=0.5,$\alpha$≈0.967532
- 4周后的权重降为5,则$\alpha$^28=0.5,$\alpha$≈0.975549
相关代码:
import datetime
import pandas as pd
ALPHA = 0.97
def get_score(order_count, days):
return order_count * pow(ALPHA, days)
df = pd.read_csv("test.xlsx")
df.columns = ['id', 'item_id', 'create_date']
df['days'] = (datetime.datetime.now() - df.create_date).astype('timedelta64[D]')
df_s = df.groupby(['item_id', 'days']).size().reset_index(name='order_count')
df_s["score"] = get_score(df_s.order_count, df_s.days)
df_m = df_s.groupby("item_id").score.sum().reset_index(name='score')
df_m.to_cvs("result.csv")
一些说明:
- 通常在计算时可以取30天的数据,原因是某个<1数字的30次方已经非常小了,计算的意义不大
- 以上的计算针对的是有热度的内容或产品,如果部分内容不随时间衰减,使用上诉公式不影响
另外以上逻辑也可在SQL中直接完成:
SELECT itemid
, SUM(order_count * pow(0.9, recency)) AS score
FROM (
SELECT mo.itemid, datediff(current_date(), mo.createdate) AS recency
, COUNT(DISTINCT mo.memberid) AS order_count
FROM db.memberorder mo
GROUP BY mo.itemid, datediff(current_date(), mo.createdate)
) t
GROUP BY itemid
ORDER BY score DESC
LIMIT 100
Reddit文章
Reddit与HackerNews类似,也是一个社会化新闻网站,Reddit对文章和评论使用了不同的排名算法,这里介绍的排序规则主要针对的是文章排序。
Reddit与HackerNews有很大的不同点就是,HackerNews文章标题前面只有一个向上的小箭头,即只能投赞成票,而Reddit的每个文章标题前会有两个箭头,即一个向上,一个像下。分别代表”赞成”与”反对”。Reddit已经把他们的所有源代码进行了公开,具体涉及到排序部分的代码如下:https://github.com/reddit/reddit/blob/master/r2/r2/lib/db/_sorts.pyx。由于此部分代码是使用Python的C语言扩展来写,下面是用Python重写的代码:
from datetime import datetime
from math import log
epoch = datetime(1970, 1, 1)
def epoch_seconds(date):
"""Returns the number of seconds from the epoch to date."""
td = date - epoch
return td.days * 86400 + td.seconds + (float(td.microseconds) / 1000000
def up_down(ups, downs):
return ups - downs
def hot(ups, downs, date):
"""The hot formula. Should match the equivalent function in postgres."""
z = up_down(ups, downs)
order = log(max(abs(z), 1), 10)
sign = 1 if z > 0 else -1 if z < 0 else 0
seconds = epoch_seconds(date) - 1134028003
return round(order + sign * seconds / 45000, 7)
从上面的代码中可以看到整个逻辑并不复杂。
分值计算公式:
$$score=\log_{10}z+\frac{yt_s}{45000}$$
其中:
- z:获得的投票数的绝对值(赞成-反对),当=0时,z=1
- y:投票方向,投票数>0时,y=1;y=0时,y=0;<0时,y=-1
- $t_s$:发布时间距离2005年12月8日07:46:43的秒数
从上面的代码级公式中我们可以了解到Reddit的排名算法主要与以下内容有关:
文章的发表时间t
t=发表时间–2005年12月8日7:46:43
在HackerNews的算法中,用来标注文章新旧程度的单位为小时,而Reddit的单位为秒,其使用Unix时间戳(从1970年1月1日到当前时间的秒数)进行的计算,代码中的1134028003代表的日期为2005年12月8日7:46:43。这个应该是Reddit这个网站的上线时间。通过上面的公式可以看到一旦帖子发表,t就是固定值,不会随时间改变,而且帖子越新,t值越大。
发表时间和话题排名的影响可以被概括如下:
- 发表时间对排名有很大影响,该算法使得新的话题比旧的话题排名靠前
- 话题的得分不会因为时间的流失而减少,但是新的话题会比旧的话题得分高。这与HackerNew的算法不同(随着时间的发展降低话题的得分)
下图展示了话题得分在好评和差评的数量不变时,随着时间而变化的情况:

赞成票与反对票的差x
x=赞成票-反对票
真是由于Reddit提供了投反对票的功能,所以可以使一些具有争议的话题会排的较后,下图展示了在好评和差评不变时,随着时间而变化的情况:
公式分解分析
上述公式可以分成两个部分来讨论:
$$\log_{10}z$$
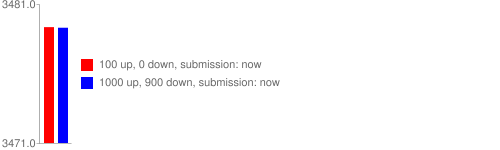
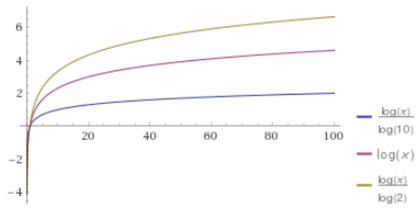
这个部分表示,赞成票超过反对票的数量越多,得分越高。需要注意的是,这里用的是以10为底的对数,意味着z=10可以得到1分,z=100可以得到2分。也就是说,前10个投票人与后90个投票人(乃至再后面900个投票人)的权重是一样的,即如果一个帖子特别受到欢迎,那么越到后面投赞成票,对得分越不会产生影响。而当反对票超过或等于赞成票,z=1,因此这个部分等于0,也就是不产生得分。
Reddit的热排序算法使用了对数函数来衡量前面的投票与其他投票的差距使其前十个好评和之后的100个,1000个投票有相同的权重。参见下面的图:
 如果不采用对数,而使用线性函数的效果如下:
如果不采用对数,而使用线性函数的效果如下:

Reddit敢于如此消弱投票的作用,其实与其庞大的流量和用户参与度相关。如果没有以上因素算法很难实现很好的推荐。
另外对数取不同的额底对于消弱的效果也是不同的。
$$\frac{yt_s}{45000}$$
这个部分表示,t越大,得分越高,即新帖子的得分会高于老帖子。它起到自动将老帖子的排名往下拉的作用。分母的45000秒,等于12.5个小时,也就是说,后一天的帖子会比前一天的帖子多得2分。结合前一部分,可以得到结论,如果前一天的帖子在第二天还想保持原先的排名,在这一天里面,它得到的净赞成票必须增加100倍。
y的作用是用来产生正分和负分。当赞成票超过反对票时,得分为正;当赞成票少于反对票时,得分为负;当两者相等,得分为0。这就保证了得到大量净赞成票的文章,会排在前列;得到大量净反对票的文章,会排在最后。投票对于总分的贡献不大,但是当投票的意见倾向发生变化时(由正面评价转向负面评价),投票对于总分的作用却是决定性(Y的取值)。
总结
关于Reddit的排名,基本上是由发表时间决定的,只有相同时段的文章才有可比性。晚半天,投票就要翻10倍,只能同时段的文章相比。只有超级受欢迎的文章才会排在最前面,有争议或者一般性的文章很难靠前。基于上述也就决定了Reddit是一个符合大众胃口的网站,并不是一个很激进可以展示少数派想法的地方。
再来看下Reddit与HackerNews的区别,到底哪一个的算法更好一些呢?其实算法并没有优劣之分,两种方法更有千秋,重要的是你打算用在什么地方。Reddit流量大,所以可以减少投票的权重,而也因为流量大,使得每篇文章在没有收到新的投票的时候无需重新计算得分,也可大大的减少服务器的运算成本。
Reddit评论
目前很多网站采用的评论排名主要有两种,即绝对好评数(好评减去差评)和好评率(好评/总评)。这两种评价方式都存在很明显的缺陷,以下为事例:
- A:好评550; 差评450
- B:好评60;差评40
- C:好评1;差评0
- D:好评9,差评1
首先是A与B比较,A的绝对好评数是550-450=100,B的绝对好评数是60-40=20,从绝对好评数比较,A的排名应该在B的前面;A的好评率为550/(450+550)=55%,B的好评率为60/(40+60)=60%,从好评率来说B的排名要比A的排名好。
再来比较下C与D,从好评率出发,C的好评率为100%,而D的好评率为9/(1+9)=90%,单纯从数据上看D的排名要比C的排名落后。对于评论排名上述的方法是否是我们所需要的呢?这样的计算才能更好的体现评论价值?正确的排名算法应该是怎样的?
我们先做如下设定:
- 每个用户的投票都是独立事件。
- 用户只有两个选择,要么投好评,要么投差评。
- 如果投票总人数为n,其中好评为k,那么好评率p就等于k/n。
如果你熟悉统计学,可能已经看出来了,p服从一种统计分布,叫做“两项分布”(binomial distribution)。
p越大,就代表这个项目的好评比例越高,越应该排在前面。但是,p的可信性,取决于有多少人投票,如果样本太小,p就不可信。由于p服从”两项分布”,因此我们可以计算出p的置信区间。所谓“置信区间”,就是说,以某个概率而言,p会落在的那个区间。比如,某个产品的好评率是80%,但是这个值不一定可信。根据统计学,我们只能说,有95%的把握可以断定,好评率在75%到85%之间,即置信区间是[75%,85%]。
通过上面的分析,我们就可以推断出,如果要给一个评论进行排名,就需要考虑一下内容:
- 计算每个评论的“好评率”
- 计算每个“好评率”的置信区间(以95%的概率)。
- 根据置信区间的下限值,进行排名。这个值越大,排名就越高。
这样做的原理是,置信区间的宽窄与样本的数量有关。比如,
- A有8张赞成票,2张反对票
- B有80张赞成票,20张反对
这两个项目的赞成票比例都是80%
- A的置信区间(假定[70%,90%])
- B的置信区间(假定[75%,85%])
B的置信区间的下限值(75%)会比A(70%)大,所以B应该排在A前面。置信区间的实质,就是进行可信度的修正,弥补样本量过小的影响。如果样本多,就说明比较可信,不需要很大的修正,所以置信区间会比较窄,下限值会比较大;如果样本少,就说明不一定可信,必须进行较大的修正,所以置信区间会比较宽,下限值会比较小。
正态区间
二项分布的置信区间有多种计算公式,最常见的是“正态区间”(Normal approximation interval),教科书里几乎都是这种方法。但是,它只适用于样本较多的情况(np>5且n(1-p)>5),对于小样本,它的准确性很差。
要了解正态区间前需要先掌握一些正态分布的知识。
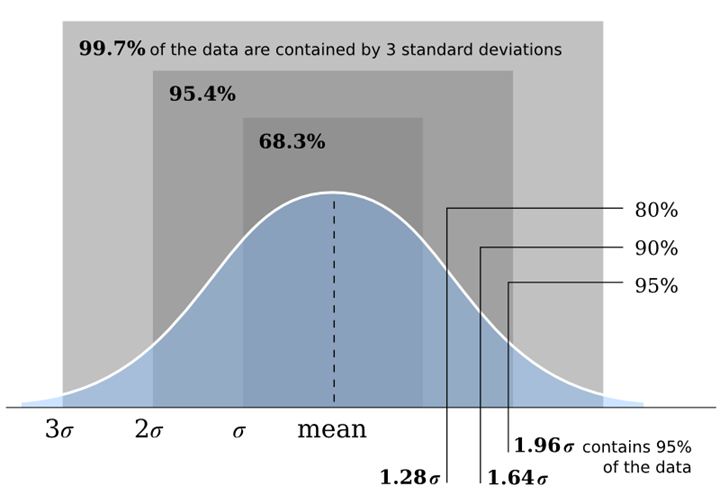
上图最右侧的0%、90%、95%为置信水平。即数据录入[a,b]区间内的概率。与此对应的1.28$\sigma$、1.64$\sigma$、1.96$\sigma$,其中\sigma为标准差,1.28、1.64、1.96为z-score(标准分位)。在正态分布中,不同的置信水平对应的z值是固定的,如下为常见的90%、95%和99%对应的z值。
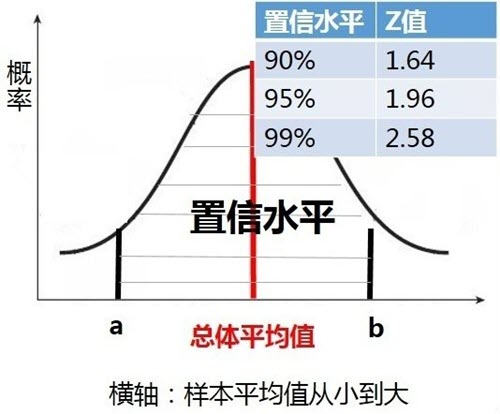
你可以通过搜索z-score table搜索到详细的Z值对应置信水平的表格,如下图:
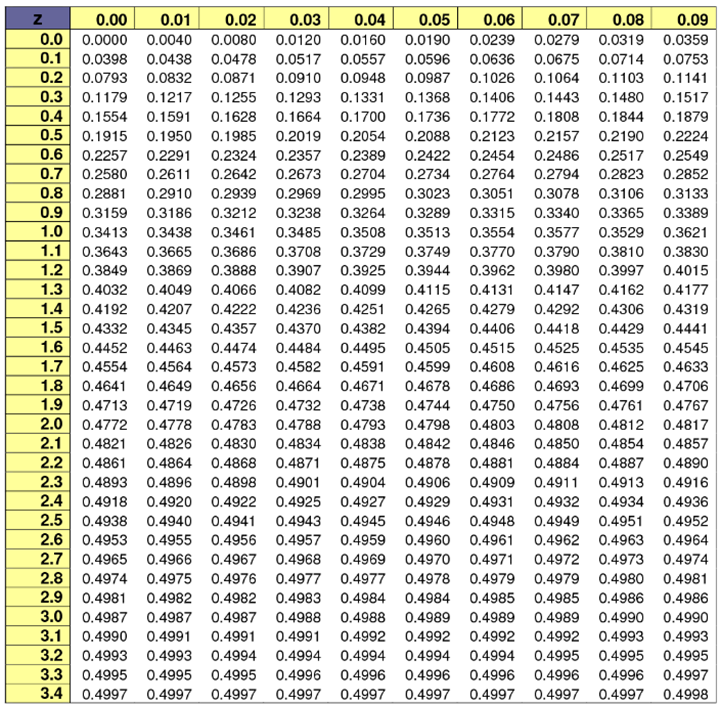
正态区间[a,b]的计算方法:
- a=总体平均值$\mu$-标准分位z*标准误差SE
- b=总体平均值$\mu$+标准分位z*标准误差SE
其中:
$$SE=\frac{S}{\sqrt{n}}$$
- SE:标准误差
- s:样本标准差
- n:样本大小
威尔逊区间
1927年,美国数学家Edwin Bidwell Wilson提出了一个修正公式,被称为威尔逊区间,很好地解决了小样本的准确性问题。Reddit目前使用的是评论算法就是基于威尔逊得分区间(Wilson score interval)。具体代码片段可从开放的源代码找到,将其转化成Python代码后:
from math import sqrt
def _confidence(ups, downs):
n = ups + downs
if n == 0:
return 0
z = 1.0 # 1.0 = 85%, 1.6 = 95%
phat = float(ups) / n
return (phat + z*z/(2*n) - z * sqrt((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n)
def confidence(ups, downs):
if ups + downs == 0:
return 0
else:
return _confidence(ups, downs)
威尔逊得分区间具体公式如下:
$$\frac{\hat{p}+\frac{1}{2n}z^2\pm z\sqrt{\frac{\hat{p}(1-\hat{p})}{n}+\frac{z^2}{4n^2}}}{1+\frac{1}{n}z^2}$$
其中:
- p是好评率
- n是总投票数
- $z$表示对应某个置信水平的z统计量,这是一个常数,可以通过查表得到。一般情况下,在95%的置信水平下,z统计量的值为96。
可以公式看到,当n的值足够大时,这个下限值会趋向$\hat{p}$。如果n非常小(投票人很少),这个下限值会大大小于$\hat{p}$。实际上,起到了降低”好评率”的作用,使得该评论的得分变小、排名下降。
威尔逊得分区并不关心一个评论的投票数,而关心好评数和投票总数或采样大小的相对关系!

上图是根据威尔逊得分区计算出来的值:一个评论有1个好评,没有差评,它的支持率是100%,但是由于数据量过小,系统还是会把它放到底部。但如果,它有10个好评,1个差评,系统可能会有足够的信息把他放到一个有着40个好评,20个差评的评论之前。因为我们基本确认当它有了40个好评的时候,它收到的差评会少于20个。最好的一点是,一旦这个算法出错了(算法有15%的失效概率),它会很快拿到更多的数据,因为它被排到了前面。
威尔逊得分区间不仅仅用于评论排名,它还适用于以下情景:
- 垃圾邮件检测:看到这个内容并将它标记成垃圾邮件的百分比有多少?
- 创建精华列表:看到这个内容并将它加星标件的百分比有多少?
- 创建最受欢应列表:看到这个内容并将它转发给朋友的百分比有多少?
说了那么多,再来看看威尔逊得分区间的缺点,从上面的分析中也很容易发现问题,即排行榜前列总是那些票数最多的项目,新项目或者冷门的项目,很难有出头机会。
另外被成为当代故事会的知乎回答的答复貌似也是采用的威尔逊得分。
IMDB
IMDB.COM是目前互联网上最为权威、系统、全面的电影资料网站,里面包括了几乎所有的电影,以及1982年以后的电视剧集。它所特有的电影评分系统深受影迷的欢迎,注册的用户可以给任何一部影片打分并加以评述,而网站又会根据影片所得平均分、选票的数目等计算得出影片的加权平均分并以此进行TOP250(最佳250部影片)和Bottom100(最差100部影片)的排行。
如果是你,你会如何进行排序?哪些维度会被你考虑在内?
- 点评数
- 点评分
以上两个因素都是正相关,如何确定哪个权重更高?比如:
- 电影A,十个人看过,全部评分均为10分
- 电影B,十万个人看过,评分平均值为8分
如何计算才能确定哪部电影更好看?有的人可能认为是A,有的人可能认为B,作为平台如何确定哪个更好?
IMDB排名算法采用的是贝叶斯定理确定的其分值。在了解贝叶斯定理前,我们想要来理清一些概念。
什么是概率?
抛一枚硬币正面向上的概率是多少?
频率学派:事件A在独立重复试验中发生的频率趋于极限p,那么这个极限就是该事件的概率。理论基础:事件本身具有某种客观的随机性。
不能重复试验的场景下的概率又是什么?
比如:苏州明天下午的概率是?
贝叶斯学派:把概率解释为对不确定的主管置信度,描述观察者知识状态在新的观测发生后如何更新。理论基础:同一件事情对于知情者而言就是「确定事件」,对于不知情者而言就是「随机事件」,随机性并不源于事件本身是否发生,而只是描述观察者对该事件的知识状态。
平均数定律
在赌场里或看到有趣的人类行为。当投骰子的人连续赢了几把的时候,有些赌徒就会认为他”手很顺”,打赌他还会继续赢。其他人说,根据”平均数定律”他接下来要输了,这样输赢才能平衡。从你的角度你认为他会赢还是会输。
在解答上述问题前,我们先来看一个数学题,抛硬币,连续三次向上,下一次抛硬币还是正面概率是多少?
概率学派:只要我们认可硬币是均匀的(正负概率各半),且为独立同分布,则结论仍然是50%。
贝叶斯学派:问题转换,你拿一个硬币,扔一百次,每当连扔出三个正面时你就把下一次投掷的结果记下来,最后你的结果里正反面各占多少?下一次投掷是正面的概率对不同的投掷次数n、连续出现正面的次数k和单次投掷出现正面的概率p作图。”扔一百次,观察连扔出三个正面后下一次的结果”对应着n=100,k=3,p=0.5,所以下一次是正面的概率约为0.46。
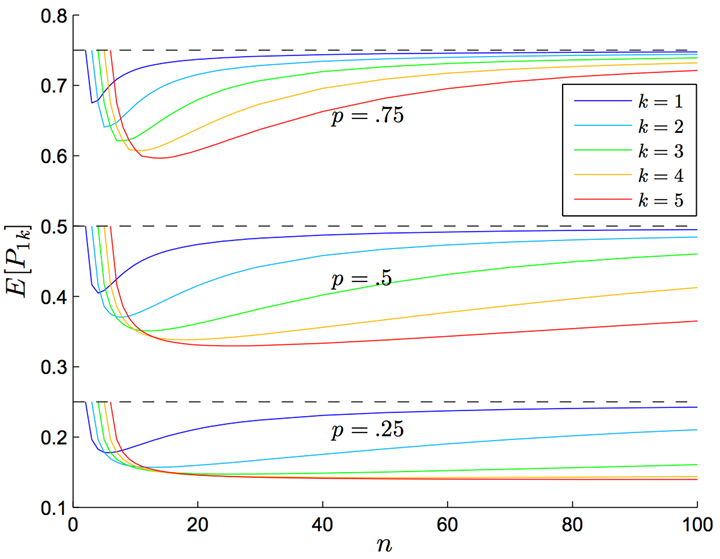
贝叶斯定理
贝叶斯定理是关于随机事件A和B的条件概率的一则定理。
$$P(A|B)=\frac{P(A)P(B|A)}{P(B)}$$
其中A以及B为随机事件,且P(B)不为零。P(A|B)是指在事件B发生的情况下事件A发生的概率。基于上式可推倒出:
$$P(B)=P(A,B)+P(A^C,B)=P(B|A)P(A)+P(B|A^C)P(A^C)$$
IMDB排名公式
$$WR=\frac{v}{v+m}R+\frac{m}{v+m}C$$
其中:
- WR,加权得分
- v,该电影的投票人数
- m,排名前250名的电影的最低投票数(人为设定的,目前好像是25000)
- R,该电影的用户投票的平均得分
- C,所有电影的平均得分(现在为9)
针对该公式的解读:
- IMDB为每部电影增加了25000张选票,并且这些选票的评分都为9。
- 假设所有电影都至少有25000张选票,那么就都具备了进入前250名的评选条件
- 假设这25000张选票的评分是所有电影的平均得分(即假设这部电影具有平均水准)
- 用现有的观众投票进行修正
- 长期来看,v/(v+m)这部分的权重将越来越大,得分将慢慢接近真实情况。
这样做拉近了不同电影之间投票人数的差异,使得投票人数较少的电影也有可能排名前列。值得注意的是,虽然很多影片在资料系统中得分很高,但由于未能达到TOP所要求的最低投票数而无法参加排行。
IMDB电影排名算法的缺陷:
- 新上映的电影短时间内评分上不去(点评量达不到要求)
- 能进入TOP250的肯定是好电影,不是所有的好电影都能进入TOP250
贝叶斯平均
把这个公式写成更一般的形式:
$$\bar{x}=\frac{C\times m+\sum_{i=1}^{n}x_i}{n+C}$$
其中:
- C,投票人数扩展的规模,是一个自行设定的常数,与整个网站的总体用户人数有关,可以等于每个项目的平均投票数。
- n,该项目的现有投票人数。
- x,该项目的每张选票的值。
- m,总体平均分,即整个网站所有选票的算术平均值。
这种算法被称为”贝叶斯平均”(Bayesian average)。因为某种程度上,它借鉴了”贝叶斯推断”(Bayesian inference)的思想:既然不知道投票结果,那就先估计一个值,然后不断用新的信息修正,使得它越来越接近正确的值。
在这个公式中,m(总体平均分)是”先验概率”,每一次新的投票都是一个调整因子,使总体平均分不断向该项目的真实投票结果靠近。投票人数越多,该项目的”贝叶斯平均”就越接近算术平均,对排名的影响就越小。因此,这种方法可以给一些投票人数较少的项目,以相对公平的排名。
“贝叶斯平均”也有缺点,主要问题是它假设用户的投票是正态分布。比如,电影A有10个观众评分,5个为五星,5个为一星;电影B也有10个观众评分,都给了三星。这两部电影的平均得分(无论是算术平均,还是贝叶斯平均)都是三星,但是电影A可能比电影B更值得看。
解决这个问题的思路是,假定每个用户的投票都是独立事件,每次投票只有n个选项可以选择,那么这就服从”多项分布”(Multinomial distribution),就可以结合贝叶斯定理,计算该分布的期望值。由于这涉及复杂的统计学知识,这里就不深入了。
问题:豆瓣的TOP250排序?
StackOverflow
StackOverflow是一个专门针对程序员的问答网站,它能解决代码开发中遇到的很多问题。StackOverflow的排序共分为两类,1个是问题排序,1个是答案排序。这里主要介绍的是关于热门问题的排序。
在分析问题前可以先考虑下,如果是你来做这个排名算法需要考虑哪些因素?
StackOverflow在开始设计热门排序规则时考虑的因素:
- 问题的投票数,StackOverflow允许用户投反对票,所以这里可以使用绝对投票数,即正面票-负面票数量。绝对数越高问题越热门。
- 答案的投票数,即是否存在一个被大量认可的答案。这里存在两种情况,被提问者认可或被其他访问者投票。多少的投票量可以认为是问题答案被认可也是需要考虑的问题。
- 问题的浏览量,或是有效浏览量,有效浏览量可以建立一个停留时间的阀值去衡量。浏览的越多则越热门。
- 问题的答案数,理论上说答案越多则问题的越热门,但这也并不绝对,有些好的问答可能只有一个好的答案。
- 问题的提问时间和问题的最近回答时间,问题的受欢迎程度应该是随时间变长而变得不热门。
- 提问者的声望和回答者的声望,声望越高的问题肯定质量越到,越值得去推荐。
在2008年8月23日的时候,StackOverflow的创始人Jeff Atwood曾经公布了一个热门问题的排名算法(链接):具体为:
$$\frac{(\log_{10} Qviews) \times 4 + \frac{Qanswers \times Qscore}{5} + sum(Ascores)}{((Qage + 1) – (\frac{Qage – Qupdated}{2}))^{1.5}} = \frac{(\log_{10} Qviews) \times 4 + \frac{Qanswers \times Qscore}{5} + sum(Ascores)}{(1 + \frac{Qage}{2} + \frac{Qupdated}{2})^{1.5}}$$
Qviews(问题的浏览次数) log(Qviews)*4
某个问题的浏览次数越多,就代表越受关注,得分也就越高。这里使用了以10为底的对数,用意是当访问量越来越大,它对得分的影响将不断变小。
Qscore(问题得分)和 Qanswers(回答的数量) (Qanswers * Qscore)/5
Qscore(问题得分)=赞成票-反对票。如果某个问题越受到好评,排名自然应该越靠前。Qanswers表示回答的数量,代表有多少人参与这个问题。这个值越大,得分将成倍放大。这里需要注意的是,如果无人回答,Qanswers就等于0,这时Qscore再高也没用,意味着再好的问题,也必须有人回答,否则进不了热点问题排行榜。
Ascores(回答得分) sum(Ascores)
一般来说,”回答”比”问题”更有意义。这一项的得分越高,就代表回答的质量越高。但是简单加总的设计还不够全面。这里有两个问题。首先,一个正确的回答胜过一百个无用的回答,但是,简单加总会导致,1个得分为100的回答与100个得分为1的回答,总得分相同。其次,由于得分会出现负值,因此那些特别差的回答,会拉低正确回答的得分。
Qage(距离问题发表的时间)和 Qupdated(距离最后一个回答的时间) ((Qage + 1) – ((Qage – Qupdated)/2))^1.5
Qage和Qupdated的单位都是小时。如果一个问题的存在时间越久,或者距离上一次回答的时间越久,Qage和Qupdated的值就相应增大。也就是说,随着时间流逝,这两个值都会越变越大,导致分母增大,因此总得分会越来越小。
此算法目前是否还继续使用或者是否改变不得而知。将其转化成Python代码为:
import time, math
def hot(Qviews, Qanswers, Qscore, Ascore, date_ask, date_active):
Qage = round((time.time() - date_ask)/3600)
Qupdated = round((time.time() - date_active)/3600)
return (math.log10(Qviews)*4 + Qanswers*Qscore/5 + Ascore)/(pow((Qage + 1) - (Qage - Qupdated)/2, 1.5))
StackOverflow热点问题的排名,与参与度(Qviews和Qanswers)和质量(Qscore和Ascores)成正比,与时间(Qage和Qupdated)成反比。以下为个人思考点:
为什么不使用”声望值”?
- 问题的质量与提问者的声望无正相关系
- 问题的答案与回答者的声望无正相关系
- 无名小辈也可以有精彩的问题与答案
提问的目的是获得正确的答案,而不是谁参与了此问题。声望值纳入容易造成,在没有声望认识加入的情况下,问题无法进入热门榜。
浏览量与分值的关系 log(Qviews)*4
这类对浏览量做了一次对数处理,主要目标应该是防止浏览量较大的问答占着榜单不动,抑制马太效应。这里再对结果*4,应该是由于10为第的对数抑制效果太大了,乘4稍微加大权重的影响。
针对此部分内容,我认为可以简化为:
$$\log_{10}{x} = \log_{b}{x} \Rightarrow b = \sqrt[4]{10} = 1.78$$
即将底数从10改为1.78,或者以2为底。
答案数和投票数与分值关系 $\frac{Qanswers \times Qscore}{5}$
这里的将答案的分值与答案数相乘,我个人认为是不适合。问题是否热门与回答数量正相关?与答案的分值正相关?这里将分数除以5,我的猜测是答案数、投票分的权重,考虑到问题答案数量普遍较少,猜想是想投票分的影响。
是否合理?
- 技术类问答,非开放性问题,往往答案只有一个,提问者的需求也仅仅需要一个答案
- Qscore=赞成票-反对票,如果这个问题存在较大的争议,赞成票与反对票接近,是否是一个热门的问题?
我建议的修改方案是:Qstatus * Qupvote:
- Qstatus:是否有答案,没有为0,有为1
- Qupvote:赞成票数量(考虑到 Stackoverflow 可能没有存赞成票数,用 Qscore 也可以)
答案投票数与分值关系 sum(Ascore)
是否合理?
- 问题 A:有 1 个答案,投票数为 10
- 问题 B:有 4 个答案,投票数为 4, 3, 2, 1
- 问题 C:有 2 个答案,投票数为 10, -5
以上问题哪个更好?从现有的公式中最好的可能是 A 和 B,实际上更高的或许应该是 AC?
建议优化方案:Ascore 只取投票数为正(Ascore>0)的答案,取每个分值平方和的开方(Square root of sum of squares):$\sqrt{x_1^2+x_2^2+…+x_n^2}$
提问时间与最后解答时间与分值关系 $(1+\frac{Qage}{2}+\frac{Qupdated}{2})^{1.5}$
- 为什么要 +1?防止问题刚提交时,公式中分母为 0
- 为什么要 ÷2?把 2 小时作为最小的时间粒度单位
- 为什么要去 5 次方?添加“重力加速度”,提升曲线的陡度
如何理解影响关系?
- 发布时间越久,分值越低
- 回答时间越久,分值越低
总体评价:StackOverflow 的排序算法非常的简陋,还有很多优化空间。
SegmentFault
SegmentFault 参考了 StackOverflow 的热门算法设置了自己的排序算法,具体排序算法如下:
热门文章
对于热门文章,使用了如下公式:
$$\frac{\lg(views)*4+recommendScore+collectScore+\ln(articleComments)}{(1+\frac{age}{2}+\frac{update}{2})^i}$$
其中
- views:浏览量,对浏览量做了一次去对数处理,主要是为了防止某些浏览量较大的文章异军突起,待在榜单迟迟不动。
- recommendScore:文章的推荐数,直接加和到分子中,作为文章热门程度的考虑因素。
- collectScore:文章的收藏数,直接加和到分子中,作为文章热门程度的考虑因素。
- articleComments:文章评论数,这个也作为一个影响文章热度的因素,不过为了降低其影响,对其作了一次取对数操作,主要是考虑到评论数量的影响力并没有上面两个的高。
- (1+age/2+update/2)^i:分母是对时间因子的考虑,宏观上来看,就是文章热度和创建时间成反比。细节上,做成了个指数函数,可以通过对 i 变量的调控来改变时间因子在对热度的影响。
- age:内容发布时间
- update:内容最后更新时间(所有时间值单位均为 h/3600)
- i:重力因子,取值的大小会直接决定热门排序(后面将介绍这点)
热门问答
对于热门问答,使用了如下公式:
$$\frac{\lg(views)*4+\frac{sum(Qanswers*answerScores+Qscore)}{5}+ln(commentScore)}{(1+\frac{age}{2}+\frac{update}{2})^i}$$
热门问答的计算参考了 StackOverflow 对于回答数量和问题得票数的处理。同时,结合我们的实际,将评论的得票数也做为一个因素加入计算。
- Qanswers/Qscore:分别是问题的答案数量和问题的得票数
- anwserScores/commentSocres:分别是该问题下所有答案的总得票数和所有评论的总得票数
- update:该问题下答案的最新更新时间
其余的变量含义和文章算法相同。
日/周/月热门
首先要明确各类不同热门内容的目的。
- 日热门的主要目的就是突出最近一天内的热门内容,更方便于内容被大家看到,文章快速地形成讨论、受关注的问题尽快得到解决;
- 周热门的主要目的很明确,就是突出过去一周内的热门内容,同时,给新产生的优秀内容机会,让其有机会进入热门列表;
- 月热门同周热门目的一样,但更需要给新内容进入列表的机会,以让内容经常更新。
所以,该怎么做呢?对于同一内容,上面的计算公式均可简化为:$\frac{s}{t^i}$
- S 是总得分指标
- t 为时间量
- i 是变量重力因子
可以看出,其热度和创建时间成反比,那么这个反比的值最终就由重力因子 i 来影响。
日热门为了突出新热内容、过滤时间过久的热门内容,需要增大重力因子,尽可能排除 24 小时之外的热门内容;周热门和月热门则需要按时间要求依次逐渐降小 i 值。
关于指数 i 值的选定,采取了估算:绘制出一定范围内时间和文章热度的指数函数的图,然后根据需求挑选满足自己条件的指数值。如下图:
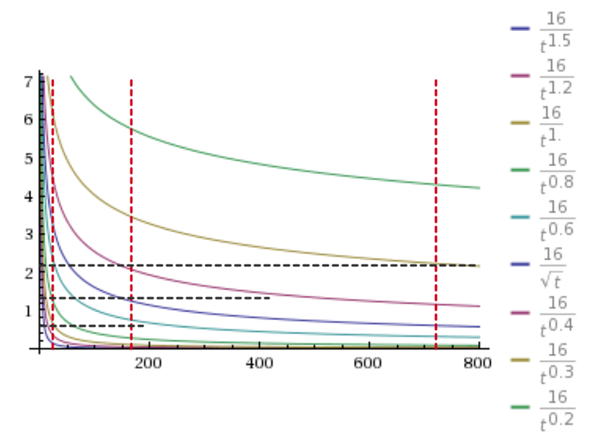
多次估值测试,最终分别将日、周、月的 i 值选取为 1.0、0.5、0.3。
参考链接:




Hacker News: 的方式, P 值为0 时, 如何处理呢?