标签传播算法（label propagation）简介
半监督学习
机器学习可以大体分为三大类：监督学习、非监督学习和半监督学习。
- 监督学习可以认为是我们有非常多的labeled标注数据来train一个模型，期待这个模型能学习到数据的分布，以期对未来没有见到的样本做预测。
- 非监督学习就是没有任何的labeled数据，就是平时所说的聚类，利用他们本身的数据分布，给他们划分类别。
- 半监督学习，顾名思义就是处于两者之间的，只有少量的labeled数据，我们试图从这少量的labeled数据和大量的unlabeled数据中学习到有用的信息。
半监督学习算法会充分的利用unlabeled数据来捕捉我们整个数据的潜在分布。它基于三大假设：
- Smoothness平滑假设：相似的数据具有相同的label。
- Cluster聚类假设：处于同一个聚类下的数据具有相同label。
- Manifold流形假设：处于同一流形结构下的数据具有相同label。
例如下图，只有两个labeled数据，如果直接用他们来训练一个分类器，例如LR或者SVM，那么学出来的分类面就是左图那样的。如果现实中，这个数据是右图那边分布的话，因为我们的labeled训练数据太少了，都没办法覆盖我们未来可能遇到的情况，左图训练的这个分类器烂的一塌糊涂、惨不忍睹。但是，如果右图那样，把大量的unlabeled数据（黑色的）都考虑进来，有个全局观念，牛逼的算法会发现，原来是两个圈圈（分别处于两个圆形的流形之上）。
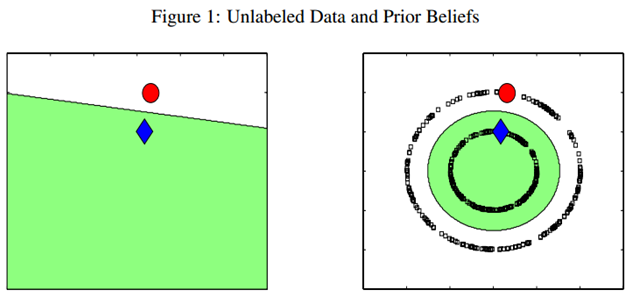
实践中，labeled数据是昂贵，很难获得的，但unlabeled数据就不是了，写个脚本在网上爬就可以了，因此如果能充分利用大量的unlabeled数据来辅助提升我们的模型学习，这个价值就非常大。半监督学习算法有很多，下面我们介绍最简单的标签传播算法（label propagation）
标签传播算法（label propagation）
标签传播算法Label Propagation Algorithm简称LPA，是机器学习中的一种常用的半监督学习(semi-supervised)方法，用于向未标记（unlabeled）样本分配标签。标签传播算法的核心思想非常简单：相似的数据应该具有相同的label。标签传播算法通过将所有样本通过相似性构建一个边有权重的图，然后各个样本在其相邻的样本间进行标签传播。因此标签传播算法在本质上就很适合用来做网络结构中的社区发现。
算法并不难理解，算法的输入是一个无向图，如下图所示：
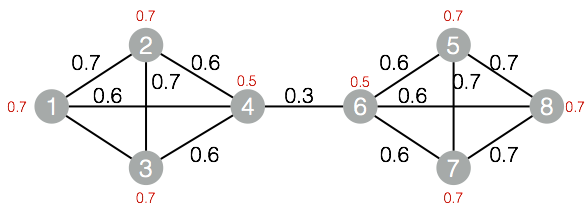
其中的红色的数字代表对应节点的权重，边上的黑色数字代表边的权重。
算法的输出如下：
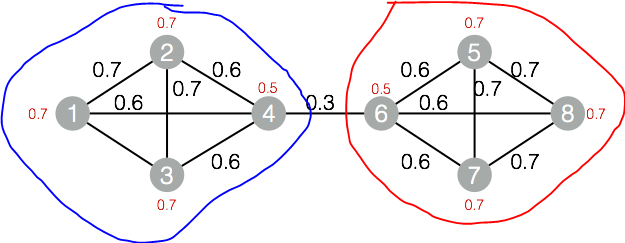
最终蓝线和红线圈起来的节点就是潜在的社区，就是聚类结果。
LPA算法优点
Label Propagation算法最大的优点是其算法逻辑比较简单，相比于优化模块度的过程，算法速度非常快。Label Propagation算法利用网络自身的结构指导标签的传播过程，在这个过程中无需优化任何函数。在算法开始前我们不必知道社区的个数，随着算法的迭代，在最终的过程中，算法将自己决定社区的个数。
LPA算法缺点
划分结果不稳定，随机性强是这个算法致命的缺点。具体体现在：
- 更新顺序：节点标签更新顺序随机，但是很明显，越重要的节点越早更新会加速收敛过程
- 随机选择：如果一个节点的出现次数最大的邻居标签不止一个时，随机选择一个标签作为自己标签。这种随机性可能会带来一个雪崩效应，即刚开始一个小小的聚类错误会不断被放大。不过话也说话来，如果相似邻居节点出现多个，可能是weight计算的逻辑有问题，需要回过头去优化weight抽象和计算逻辑
标签传播算法（label propagation）算法原理
Label Propagation算法是一种基于标签传播的局部社区划分算法。对于网络中的每一个节点，在初始阶段，Label Propagation算法对每个节点初始化一个唯一的标签，在每次的迭代过程中，每个节点根据与其相连的节点所属的标签改变自己的标签，更改的原则是选择与其相连的节点中所属标签最多的社区标签为自己的社区标签，这便是标签传播的含义。随着社区标签不断传播，最终，连接紧密的节点将有共同的标签。
Label Propagation算法包括两大步骤：1）构造相似矩阵；2）标签传播。
构建相似矩阵
LP算法是基于Graph的，因此我们需要先构建一个图。我们为所有的数据构建一个图，图的节点就是一个数据点，包含labeled和unlabeled的数据。节点i和节点j的边表示他们的相似度。这个图的构建方法有很多，这里我们假设这个图是全连接的，节点i和节点j的边权重为：
$$w_{ij}=\exp(-\frac{\left\|x_i-x_j\right\|^2}{\alpha^2})$$
这里，$\alpha$是超参。
还有个非常常用的图构建方法是knn图，也就是只保留每个节点的k近邻权重，其他的为0，也就是不存在边，因此是稀疏的相似矩阵。
标签传播
对于Label Propagation算法，假设对于节点x，其邻居节点为，对于每一个节点，都有其对应的标签，标签代表的是该节点所属的社区。在算法迭代的过程中，节点x根据其邻居节点更新其所属的社区。
在初始阶段，令每一个节点都属于唯一的社区，当社区的标签在节点间传播时，紧密相连的节点迅速取得一致的标签。具体过程如图：
在图中所示的标签传播的过程中，对于c节点，在选择了与a节点一致的标签后，与d节点相邻的节点中，属于a社区的节点最多，因此c节点的标签也被设置成a，这样的过程不断持续下去，直到所有可能聚集到一起的节点都具有了相同的社区标签，此时，图中的所有节点的标签都变成了a。在传播过程的最终，具有相同社区标签的节点被划到相同的社区中成为一个个独立的社区。
在标签传播的过程中，节点的标签是根据其邻接节点的标签进行更新的，如在图中，与节点c相邻的节点分别为a、b和d。节点的标签的更新过程可以分为两种，即同步更新和异步更新。
同步更新是指对于节点x，在第t代时，根据其所有邻居节点在第t-1代时的社区标签，对其标签进行更新。即：
$$C_x(t)=f(C_{x_1}(t-1),C_{x_2}(t-1),….C_{x_k}(t-1))$$
其中，$C_x(t)$表示的是节点x在第t代时的社区标签。函数f表示的是取的参数节点中所有社区个数最大的社区。同步更新的方法存在一个问题，即对于一个二分或者近似二分的网络来说，这样的结构会导致标签的震荡，如下图：
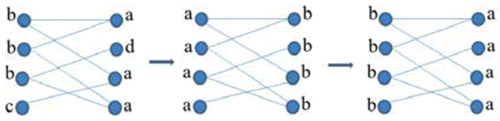图中，在第一步的更新中，若左侧节点的标签更改为a，右侧节点的标签更改为b，在第二步中，左侧的节点又会更改为b，右侧的节点又会更改为a，如此往复，两边的标签会在社区标签a和b间不停地震荡。
对于异步更新方式，其更新公式为：
$$C_x(t)=f(C_{x_{i1}}(t),…,C_{x_{im}}(t),C_{x_{i(m+1)}}(t-1),…,C_{x_{ik}}(t-1))$$
其中，邻居节点$x_{i1},…,x_{im}$的社区标签在第t代已经更新过，则使用其最新的社区标签。而邻居节点$x_{i(m+1)},…,x_{ik}$在第t代时还没有更新，则对于这些邻居节点还是用其在第（t-1）代时的社区标签。
算法迭代终止条件
当网络中的每一个节点所属的社区不再改变的时候迭代就可以停止了，对于每一个节点，在其所有的邻居节点所属当前社区中，其所属的社区标签是最大的，即：如果用$C_1,…,C_p$来表示社区标签，$d_i^{C_j}$表示节点i所有邻居节点中社区标签为$C_j$的个数，则算法终止条件为：对于每一个节点i，如果节点i的社区标签为$C_m$，则：$d_i^{C_m}>=d_j^{C_j}$这样就可以获得最终的社区。但是社区不是唯一的。
标签传播算法（label propagation）的Python实现
def label_propagation(vector_dict, edge_dict):
'''标签传播
input: vector_dict(dict)节点：社区
edge_dict(dict)存储节点之间的边和权重
output: vector_dict(dict)节点：社区
'''
# 初始化，设置每个节点属于不同的社区
t = 0
# 以随机的次序处理每个节点
while True:
if (check(vector_dict, edge_dict) == 0):
t = t + 1
print("iteration:", t)
# 对每一个node进行更新
for node in vector_dict.keys():
adjacency_node_list = edge_dict[node] # 获取节点node的邻接节点
vector_dict[node] = get_max_community_label(vector_dict, adjacency_node_list)
print(vector_dict)
else:
break
return vector_dict
def get_max_community_label(vector_dict, adjacency_node_list):
'''得到相邻接的节点中标签数最多的标签
input: vector_dict(dict)节点：社区
adjacency_node_list(list)节点的邻接节点
output: 节点所属的社区
'''
label_dict = {}
for node in adjacency_node_list:
node_id_weight = node.strip().split(":")
node_id = node_id_weight[0] # 邻接节点
node_weight = int(node_id_weight[1]) # 与邻接节点之间的权重
if vector_dict[node_id] not in label_dict:
label_dict[vector_dict[node_id]] = node_weight
else:
label_dict[vector_dict[node_id]] += node_weight
# 找到最大的标签
sort_list = sorted(label_dict.items(), key=lambda d: d[1], reverse=True)
return sort_list[0][0]
def check(vector_dict, edge_dict):
'''检查是否满足终止条件
input: vector_dict(dict)节点：社区
edge_dict(dict)存储节点之间的边和权重
output: 是否需要更新
'''
for node in vector_dict.keys():
adjacency_node_list = edge_dict[node] # 与节点node相连接的节点
node_label = vector_dict[node] # 节点node所属社区
label = get_max_community_label(vector_dict, adjacency_node_list)
if node_label == label: # 对每个节点，其所属的社区标签是最大的
continue
else:
return 0
return 1
def loadData(filePath):
f = open(filePath)
vector_dict = {}
edge_dict = {}
for line in f.readlines():
lines = line.strip().split(" ")
for i in range(2):
if lines[i] not in vector_dict:
vector_dict[lines[i]] = int(lines[i])
edge_list = []
if len(lines) == 3:
edge_list.append(lines[1-i] + ":" + lines[2])
else:
edge_list.append(lines[1-i] + ":" + "1")
edge_dict[lines[i]] = edge_list
else:
edge_list = edge_dict[lines[i]]
if len(lines) == 3:
edge_list.append(lines[1-i] + ":" + lines[2])
else:
edge_list.append(lines[1-i] + ":" + "1")
edge_dict[lines[i]] = edge_list
return vector_dict, edge_dict
if __name__ == '__main__':
filePath = './data/label_data.txt'
vector, edge = loadData(filePath)
print(vector)
print(edge)
vector_dict = label_propagation(vector, edge)
print(vector_dict)
cluster_group = dict()
for node in vector_dict.keys():
cluster_id = vector_dict[node]
print("cluster_id, node", cluster_id, node)
if cluster_id not in cluster_group.keys():
cluster_group[cluster_id] = [node]
else:
cluster_group[cluster_id].append(node)
print(cluster_group)
测试数据:https://pan.baidu.com/s/1LAAKaJBuf6k1LA8jCbpulA 提取码:zki5
参考链接：
