格兰杰因果关系检验简介
格兰杰因果关系检验(英语:Granger causality test)是一种假设检定的统计方法,检验一组时间序列x是否为另一组时间序列y的原因。它的基础是回归分析当中的自回归模型。回归分析通常只能得出不同变量间的同期相关性;自回归模型只能得出同一变量前后期的相关性;但诺贝尔经济学奖得主克莱夫·格兰杰(Clive Granger)于1969年论证,在自回归模型中透过一系列的检定进而揭示不同变量之间的时间落差相关性是可行的。
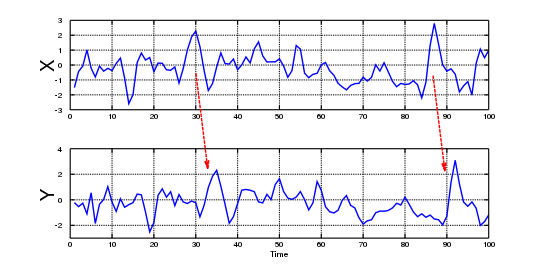
格兰杰本人在其2003年获奖演说中强调了其引用的局限性,以及”很多荒谬论文的出现”。格兰杰因果关系检验的结论只是一种统计估计,不是真正意义上的因果关系,不能作为肯定或否定因果关系的根据。同时,格兰杰因果关系检验也有一些不足之处,如并未考虑干扰因素的影响,也未考虑时间序列间非线性的相互关系。
格兰杰因果关系检验的是”统计学意义上”的因果性(时间上的先后)。和我们日常语言里说的因果性不是一回事。从统计的角度,因果关系是通过概率或者分布函数的角度体现出来的:在宇宙中所有其它事件的发生情况固定不变的条件下,如果一个事件A的发生与不发生对于另一个事件B的发生的概率(如果通过事件定义了随机变量那么也可以说分布函数)有影响,并且这两个事件在时间上又先后顺序(A前B后),那么我们便可以说A是B的原因。
这里的原因不等于生活中常说的原因,比如夏天下雷阵雨前会有很多蜻蜓飞来飞去,从统计学上存在相关因果关系,但是并不能说蜻蜓飞来飞去是导致下雨的原因。反而可以说下雨时蜻蜓飞来飞去的原因。Granger causality所做的,是观测到某些候选变量和目标变量,看某个候选变量是否有对目标变量的不可(被其他观测到的候选变量)替代的预测能力。
格兰杰因果关系检验原理
格兰杰因果关系检验的基本观念在于:未来的事件不会对目前与过去产生因果影响,而过去的事件才可能对现在及未来产生影响。也就是说,如果我们试图探讨变量x是否对变量y有因果影响,那么只需要估计x的滞后期是否会影响y的现在值,因为x的未来值不可能影响y的现在值。假如在控制了y变量的过去值以后,x变量的过去值仍能对Y变量有显著的解释能力,我们就可以称x能”Granger影响”(Granger-cause)y。
早期因果性是简单通过概率来定义的,即如果 P(B|A)>P(B)那么A就是B的原因(Suppes,1970);然而这种定义有两大缺陷:
- 没有考虑时间先后顺序
- 从P(B|A)>P(B)由条件概率公式马上可以推出 P(A|B)>P(A),显然上面的定义就自相矛盾了。
事实上,以上定义还有更大的缺陷,就是信息集的问题。严格讲来,要真正确定因果关系,必须考虑到完整的信息集,也就是说,要得出”A是B的原因”这样的结论,必须全面考虑宇宙中所有的事件,否则往往就会发生误解。最明显的例子就是若另有一个事件C,它是A和B的共同原因,考虑一个极端情况:若 P(A|C)=1,P(B|C)=1,那么显然有 P(B|AC)=P(B|C),此时可以看出A事件是否发生与B事件已经没有关系了。
因此,Granger(1980)提出了因果关系的定义,他的定义是建立在完整信息集以及发生时间先后顺序基础上的。至于判断准则,也在逐步发展变化:
最初是根据分布函数(条件分布)判断,注意$\Omega_{n}$是到n期为止宇宙中的所有信息,$Y_n$为到n期为止所有的$Y_{t}\,(t=1\cdots n)$,$X_{n+1}$为第n+1期X的取值,$\Omega_{n}-Y_{n}$为除Y之外的所有信息。
$$F(X_{n+1}|\Omega_{n})\neq F(X_{n+1}|(\Omega_{n}-Y_{n}))$$
后来认为宇宙信息集是不可能找到的,于是退而求其次,找一个可获取的信息集J来替代$\Omega$:
$$F(X_{n+1}|J_{n})\neq F(X_{n+1}|(J_{n}-Y_{n}))$$
再后来,大家又认为验证分布函数是否相等实在是太复杂,于是再次退而求其次,只是验证期望是否相等(这种叫做均值因果性,上面用分布函数验证的因果关系叫全面因果性):
$$E(X_{n+1}|J_{n})\neq E(X_{n+1}|(J_{n}-Y_{n}))$$
也有一种方法是验证Y的出现是否能减小对$X_{n+1}$的预测误差,即:
$$\sigma^{2}(X_{n+1}|J_{n})<\sigma^{2}(X_{n+1}|(J_{n}-Y_{n}))$$
最后一种方法已经接近我们最常用的格兰杰因果检验方法,统计上通常用残差平方和来表示预测误差,于是常常用X和Y建立回归方程,通过假设检验的方法(F检验)检验Y的系数是否为零。
可以看出,我们所使用的Granger因果检验与其最初的定义已经偏离甚远,削减了很多条件(并且由回归分析方法和F检验的使用我们可以知道还增强了若干条件),这很可能会导致虚假的因果关系。因此,在使用这种方法时,务必检查前提条件,使其尽量能够满足。此外,统计方法并非万能的,评判一个对象,往往需要多种角度的观察。正所谓”兼听则明,偏听则暗”。诚然真相永远只有一个,但是也要靠科学的探索方法。
格兰杰因果关系检验的步骤描述
- 准备工作:一开始要用几个滞后期来建立模型,需要研究者的评估,通常使用赤池信息量准则(英语:Akaike information criterion、简称AIC)或贝叶斯信息量准则(英语:Bayesian information criterion、简称BIC)来判断。
- 格兰杰因果关系检验的第一步是建立用y的滞后期来预测y的自回归模型。此际,如果时间序列y是广义平稳的,则可以直接使用滞后期。如果不平稳,就必须对不平稳的时间序列先做(一阶或更多阶)差分,直到得出平稳时间数列。
- 如果发现y的某期滞后期在回归分析中具有显著性(根据t检定的p值来判断),且这期滞后期加入模型后可提高回归模型的解释力(根据回归分析的F检定),这个滞后期便被留在模型中。
- 然后进一步加入x(或$\Delta x$)的滞后期来扩充回归模型。关于平稳时间序列的要求、某期滞后期留在模型中的条件,同上述y的处理。
- 当且仅当(充分必要)没有任何解释变项x(或$\Delta x$)的滞后期被留在模型中,便无法拒绝无格兰杰因果关系的零假设。
- 研究人员希望发现明显的证据,比如x是y的格兰杰原因但反之不成立,便能做出因果关系的推论。然而在实际操作中也可能会发现没有变量是对方的格兰杰原因,或者x和y两个变量互为格兰杰原因。
格兰杰因果关系检验的数学定义:
1.令x和y为广义平稳序列。如要检测x非y的格兰杰原因之零假设,首先引入y的滞后期建立y的自回归模型(AR model on y):
$$y_{t}=a_{0}+a_{1}y_{t-1}+a_{2}y_{t-2}+…+a_{m}y_{t-m}+residual_{t}$$
所有的y滞后期中:在回归分析中具有显著性(根据t-统计值的p值来判断)的,且这期滞后期加入模型后可提高回归模型的解释力(根据回归分析的F检定)的--将被留在模型中。m表示的是y变量滞后期中检定为显著的时间上最早一个。
2.接着,引入x的滞后期建立增广回归模型:
$$y_{t}=a_{0}+a_{1}y_{t-1}+a_{2}y_{t-2}+…a_{m}y_{t-m}+b_{p}x_{t-p}+…+b_{q}x_{t-q}+residual_{t}$$
所有的x滞后期中:在回归分析中具有显著性(根据学生t检验的p值来判断)的,且这期滞后期加入模型后可提高回归模型的解释力(根据回归分析的F检定)的--将被留在模型中。在以上增广回归模型中,p代表x变量滞后期中检定为显著的时间上最早一个,q则是x变量滞后期中检定为显著的时间上最近一个。
3.如果没有任何x的滞后期被留在模型中,无格兰杰因果关系的零假设就成立。
格兰杰因果关系检验的执行步骤:
第一步:检验原假设”H0:X不是引起Y变化的Granger原因”。首先,估计下列两个回归模型:
- 无约束回归模型(u):$Y_t=\alpha_0+\sum_{i=1}^{p}\alpha_iY_{t-i}+\sum_{i=1}^{q}\beta_iX_{t-i}+\varepsilon_t$
- 无约束回归模型(r):$Y_t=\alpha_0+\sum_{i=1}^{p}\alpha_iY_{t-i}+\varepsilon_t$
式中,$\alpha_0$表示常数项;p和q分别为变量Y和X的最大最后期数,通常可以取稍大一些,$\varepsilon_t$为白噪声。然后用这两个回归模型的残差平方和$RSS_u$和$RSS_r$构造F统计量:
$$F=\frac{(RSS_r-RSS_u)/q}{RSS_u/(n-p-q-1)}\sim F(q,n-p-q-1)$$
其中,n为样本容量。
检验元假设“$H_0$:X不是引起Y变化的Granger原因”(等价于检验$H_0:\beta_1=\beta_2=…=\beta_q=0$)是否成立。
如果$F\geq F_{\alpha}\quad(q,n-p-q-1)$,则$\beta_1,\beta_2,…,\beta_q$显著不为0,因拒绝假设“H0:X不是引起Y变化的Granger原因”,反之,则不能拒绝假设“H0:X不是引起Y变化的Granger原因”。
第二步:将Y与X的位置交换,按同样的方法检验原假设“H0:Y不是引起X变化的Granger原因”。
第三步:要得到“X是Y的Granger原因”的结论,必须同时拒绝原假设“H0:X不是引起Y变化的Granger原因”和接受原假设“H0:Y不是引起X变化的Granger原因”。
格兰杰因果关系检验的Python实现
Python的statsmodels中就带有Granger causality test。该方法接收一个包含2列的2维的数组作为主要参数:
- 第一列是当前要预测未来值的序列A,第二列是另一个序列B,该方法就是看B对A的预测是否有帮助。该方法的零假设是:B对A没有帮助。如果所有检验下的P-Values都小于显著水平0.05,则可以拒绝零假设,并推断出B确实对A的预测有用。
- 第二个参数maxlag是设定测试用的lags的最大值。
测试数据:
| Epoch time | Open | High | Low | Close | Vol |
| 1486094520 | 808.11 | 808.11 | 808.11 | 808.11 | 100 |
| 1486094580 | 809.45 | 809.45 | 809.45 | 809.45 | 100 |
| 1486094820 | 809.99 | 809.99 | 809.99 | 809.99 | 100 |
| 1486095540 | 811.45 | 811.45 | 811.45 | 811.45 | 100 |
| 1486095840 | 811.3 | 811.3 | 811.01 | 811.01 | 300 |
| 1486095900 | 810.76 | 810.76 | 810.76 | 810.76 | 100 |
| 1486096200 | 812 | 812 | 812 | 812 | 100 |
代码示例:
import pandas as pd
from statsmodels.tsa.stattools import grangercausalitytests
df = pd.read_excel("stock.xlsx")
grangercausalitytests(df[['Open', 'Close']], maxlag=1, addconst=True, verbose=True)
返回结果:
Granger Causality number of lags (no zero) 1 ssr based F test: F=1.6692 , p=0.2869 , df_denom=3, df_num=1 ssr based chi2 test: chi2=3.3385 , p=0.0677 , df=1 likelihood ratio test: chi2=2.6543 , p=0.1033 , df=1 parr F test amete: F=1.6692 , p=0.2869 , df_denom=3, df_num=1
结果解读:
- number of lags (no zero) 1:当lags为1时的检测结果
- ssr based F test:残差平方和F检验
- ssr based chi2 test:残差平方和卡方检验
- likelihood ratio test:似然比检验结果
- parr F test amete:参数F检验结果
格兰杰因果关系检验结果可视化呈现:
import pandas as pd
from statsmodels.tsa.stattools import grangercausalitytests
import matplotlib.pyplot as plt
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong']
mpl.rcParams['axes.unicode_minus'] = False
plt.style.use("ggplot")
result = grangercausalitytests(df[["col1", "col2"]], maxlag=10, addconst=True, verbose=True)
result_list = []
for lag in result:
for test in result[lag][0]:
lag_info = {}
lag_info["lag"] = lag
lag_info["p_value"] = result[lag][0][test][1]
lag_info["test_type"] = test
result_list.append(lag_info)
test_result = pd.DataFrame(result_list)
fig = plt.figure(figsize=(12, 6))
for t in test_result['test_type'].unique():
t_data = test_result[test_result['test_type'] == t]
plt.plot(t_data['lag'], #x轴数据
t_data['p_value'], #y轴数据
linestyle='-', #折线类型
linewidth=2, #折线宽度
color='b', #折线颜色
marker='o', #点的形状
markersize=6, #点的大小
markeredgecolor='r', #点的边框色
markerfacecolor='r') #点的填充色
plt.axhline(y=0.05, color='c', linestyle='--')
plt.title('格兰杰因果关系检验结果')
plt.xlabel('lag')
plt.ylabel('p_value')
plt.show()
效果如下:
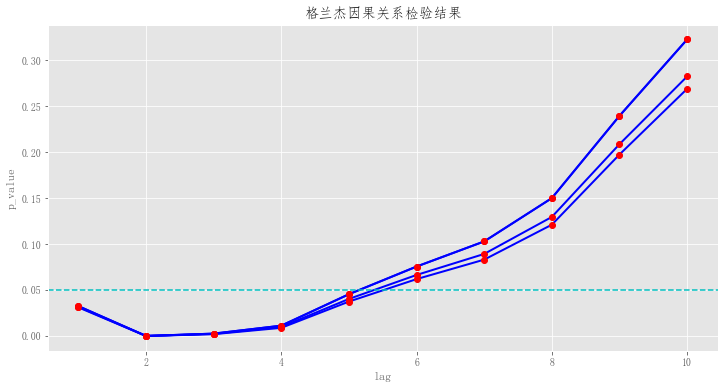 文档地址:statsmodels.tsa.stattools.grangercausalitytests
文档地址:statsmodels.tsa.stattools.grangercausalitytests
参考链接:



请问,上图代码代码中是否只做了close不是open的格兰杰因果检验,需要将CLOSE 与open的顺序对调做open不是close的格兰杰因果检验