什么是信息熵?
信息是我们一直在谈论的东西,但信息这个概念本身依然比较抽象。在百度百科中的定义:信息,泛指人类社会传播的一切内容,指音讯、消息、通信系统传输和处理的对象。但信息可不可以被量化,怎样量化?答案当然是有的,那就是“信息熵”。早在1948年,香农(Shannon)在他著名的《通信的数学原理》论文中指出:“信息是用来消除随机不确定性的东西”,并提出了“信息熵”的概念(借用了热力学中熵的概念),来解决信息的度量问题。在信息世界,熵越高,则能传输越多的信息,熵越低,则意味着传输的信息越少。
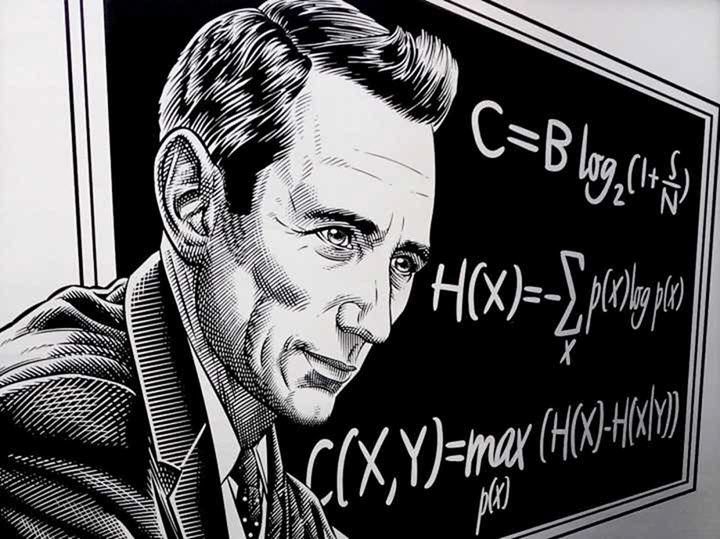
熵的概念首先在热力学中引入,用于表述热力学第二定律。在1948年,克劳德·艾尔伍德·香农将热力学的熵,引入到信息论,因此它又被称为香农熵。信息熵的定义公式:
$$H(X)=-\sum_{x\in\chi}p(x)\log{p(x)}$$
并且规定$0\log(0)=0$。熵的单位取决于定义用到对数的底。如果是以2为底数,单位是bit;如果以e为底数,单位是nat;如果以10为底数,单位是det;
香农给出的信息熵的三个性质:
- 单调性,发生概率越高的事件,其携带的信息量越低;
- 非负性,信息熵可以看作为一种广度量,非负性是一种合理的必然;
- 累加性,即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和,这也是广度量的一种体现。
为什么信息熵是这样?
- 假设存在一个随机变量$x$,当我们观测到该随机变量的一个样本时,我们可以接受到多少信息量呢?毫无疑问,当我们被告知一个极不可能发生的事情发生了,那我们就接收到了更多的信息;而当我们观测到一个非常常见的事情发生了,那么我们就接收到了相对较少的信息量。因此信息的量度应该依赖于概率分布$p(x)$,所以说熵h(x)的定义应该是概率的单调函数。
- 假设两个随机变量$x$和$y$是相互独立的,那么分别观测两个变量得到的信息量应该和同时观测两个变量的信息量是相同的,即:$h(x+y)=h(x)+h(y)$。而从概率上来讲,两个独立随机变量就意味着$p(x,y)=p(x)p(y)$,而唯一能够满足由乘法公式变为加法公式的函数即为log函数,所以此处可以得出结论熵的定义$h$应该是概率$p(x)$的log函数。因此一个随机变量的熵可以使用如下定义:$h(x)=-\log{p(x)}$。此处的负号仅仅是用来保证熵(即信息量)是正数或者为零。而log函数基的选择是任意的(信息论中基常常选择为2,因此信息的单位为比特bits;而机器学习中基常常选择为自然常数,因此单位常常被称为nats)。
- 最后,我们用熵来评价整个随机变量$x$平均的信息量,而平均最好的量度就是随机变量的期望,即熵的定义如下:$$H(X)=-\sum_{x\in\chi}p(x)\log{p(x)}$$
信息量在是作为信息“多少”的度量,这里的信息就是你理解的信息,比如一条新闻,考试答案等等。假设我们听到了两件事,分别如下:
- 事件A:巴西队进入了2018世界杯决赛圈。
- 事件B:中国队进入了2018世界杯决赛圈。
仅凭直觉来说,事件B的信息量比事件A的信息量要大。究其原因,是因为事件A发生的概率很大,事件B发生的概率很小。所以当越不可能的事件发生了,我们获取到的信息量就越大。越可能发生的事件发生了,我们获取到的信息量就越小。那么:
- 信息量和事件发生的概率相关,事件发生的概率越低,传递的信息量越大
- 信息量应当是非负的,必然发生的事件的信息量为零(必然事件是必然发生的,所以没有信息量。几乎不可能事件一旦发生,具有近乎无穷大的信息量。)
- 两个事件的信息量可以相加,并且两个独立事件的联合信息量应该是他们各自信息量的和
用信息量来理解何为“干货分享”与理解“水货分享”:
- 干货:观点独特,有实用价值的信息
- 水货:人人都明白,放着四海皆准的大道理
使用信息熵求解问题
1000桶水,其中一桶有毒,猪喝毒水后会在15分钟内死去,想用一个小时找到这桶毒水,至少需要几头猪?
限制条件:
- 一滴毒水足以导致一头猪的死亡。死亡时间为15分钟内不确定的某个时间点。
- 其死亡只是毒水导致的,不会有其他因素导致死亡。
- 猪的承水量无穷大,且假设饮一桶花费时间为零。
使用信息熵求解:
- 在1000桶水中找一桶水,需要的信息量是$-\log(\frac{1}{1000})$
- 而一头猪所能提供的信息是它在什么时间死(未死、0-15分钟、15-30分钟、30-45分钟、45-60分钟),因此能提供的信息量是$-\log(\frac{1}{5})$
- 求$-\log(\frac{1}{1000})\leq-n\log(\frac{1}{5})$可得,n>4.29203即,5头猪即可。
如何设置实验:
- 将1000桶水按5进制编号,将五头猪对应到每一位。
- 首先喂每头猪5进制编号下该位数为0的水。15分钟内,如果某头猪死了,那么有毒的水该位就是0;
- 然后过15分钟后,再喂还存活的猪5进制编号下该位数为1的水。15-30分钟内,如果某头猪死了,那么有毒的水该位就是1。
- 以此类推,于是在一个小时内我们就可以判断有毒的水的编号在5进制下每一位是多少,从而找到这桶水。
数据压缩与信息熵
香农第一定律,即信源编码定律,简单来说就是教会人类如何用数学方式将信息编码。压缩的理论基础是信息论。从信息论的角度来看,压缩就是去掉信息中的冗余,即保留不确定的信息,去掉确定的信息(可推知的),也就是用一种更接近信息本质的描述来代替原有冗余的描述。这个本质的东西就是信息量(即不确定因素)。压缩可分为两大类:
- 第一类压缩过程是可逆的,也就是说,从压缩后能够完全恢复,信息没有任何丢失,称为无损压缩
- 第二类压缩过程是不可逆的,无法完全恢复,信息有一定的丢失,称为有损压缩。
选择哪一类压缩,要折衷考虑,尽管我们希望能够无损压缩,但是通常有损压缩的压缩比无损压缩的高。
压缩原理其实很简单,就是找出那些重复出现的字符串,然后用更短的符号代替,从而达到缩短字符串的目的。比如,有一篇文章大量使用”中华人民共和国”这个词语,我们用”中国”代替,就缩短了5个字符,如果用”华”代替,就缩短了6个字符。事实上,只要保证对应关系,可以用任意字符代替那些重复出现的字符串。本质上,所谓”压缩”就是找出文件内容的概率分布,将那些出现概率高的部分代替成更短的形式。所以,内容越是重复的文件,就可以压缩地越小。比如,”ABABABABABABAB”可以压缩成”7AB”。相应地,如果内容毫无重复,就很难压缩。极端情况就是,遇到那些均匀分布的随机字符串,往往连一个字符都压缩不了。比如,任意排列的10个阿拉伯数字(5271839406),就是无法压缩的;再比如,无理数(比如π)也很难压缩。压缩就是一个消除冗余的过程,相当于用一种更精简的形式,表达相同的内容。可以想象,压缩过一次以后,文件中的重复字符串将大幅减少。好的压缩算法,可以将冗余降到最低,以至于再也没有办法进一步压缩。所以,压缩已经压缩过的文件(递归压缩),通常是没有意义的。
压缩可以分解成两个步骤:
- 第一步是得到文件内容的概率分布,哪些部分出现的次数多,哪些部分出现的次数少
- 第二步是对文件进行编码,用较短的符号替代那些重复出现的部分
第一步的概率分布一般是确定的,现在就来考虑第二步,怎样找到最短的符号作为替代符。如果文件内容只有两种情况(比如扔硬币的结果),那么只要一个二进制位就够了,1 表示正面,0 表示表示负面。如果文件内容包含三种情况,那么最少需要两个二进制位。如果文件内容包含六种情况,那么最少需要三个二进制位。一般来说,在均匀分布的情况下,假定一个字符(或字符串)在文件中出现的概率是 p,那么在这个位置上最多可能出现 $\frac{1}{p}$ 种情况。需要 $\log_2(\frac{1}{p})$ 个二进制位表示替代符号。
这个结论可以推广到一般情况。假定文件有 n 个部分组成,每个部分的内容在文件中的出现概率分别为 $p_1,p_2,…,p_n$。那么,替代符号占据的二进制最少为下面这个式子。
$$\log_2(\frac{1}{p_1})+\log_2(\frac{1}{p_2})+…+\log_2(\frac{1}{p_n})=\sum\log_2(\frac{1}{p_n})$$
这可以被看作一个文件的压缩极限。
霍夫曼编码
霍夫曼编码(英语:Huffman Coding),又译为哈夫曼编码、赫夫曼编码,是一种用于无损数据压缩的熵编码(权编码)算法。由美国计算机科学家大卫·霍夫曼(David Albert Huffman)在 1952 年发明。
在计算机数据处理中,霍夫曼编码使用变长编码表对源符号进行编码,出现频率较高的源符号采用较短的编码,出现频率较低的符号采用较长的编码,使编码之后的字符串字符串的平均长度、期望值降低,以达到无损压缩数据的目的。
举个例子,现在我们有一字符串:this is an example of a huffman tree
这串字符串有 36 个字符,如果按普通方式存储这串字符串,每个字符占据 1 个字节,则共需要 36*1*8=288 bit。
经过分析我们发现,这串字符串中各字母出现的频率不同,如果我们能够按如下编码:
| 字母 | 频率 | 编码 |
| space | 7 | 111 |
| a | 4 | 010 |
| e | 4 | 000 |
| f | 3 | 1101 |
| h | 2 | 1010 |
| i | 2 | 1000 |
| m | 2 | 0111 |
| n | 2 | 0010 |
| s | 2 | 1011 |
| t | 2 | 0110 |
| l | 1 | 11001 |
| o | 1 | 00110 |
| p | 1 | 10011 |
| r | 1 | 11000 |
| u | 1 | 00111 |
| x | 1 | 10010 |
编码这串字符串,只需要:(7+4+4)*3+(3+2+2+2+2+2+2)*4+(1+1+1+1+1+1)*5=45+60+30=135 bit
单单这串字符串,就压缩了 288-135=153 bit。那么,我们如何获取每个字符串的编码呢?这就需要哈夫曼树了。源字符编码的长短取决于其出现的频率,我们把源字符出现的频率定义为该字符的权值。
假设有 n 个权值 $\{w_1,w_2,w_3,w_4…,w_n\}$,构造一棵有 n 个节点的二叉树,若树的带权路径最小,则这颗树称作哈夫曼树。这里面涉及到几个概念,我们由一棵哈夫曼树来解释:
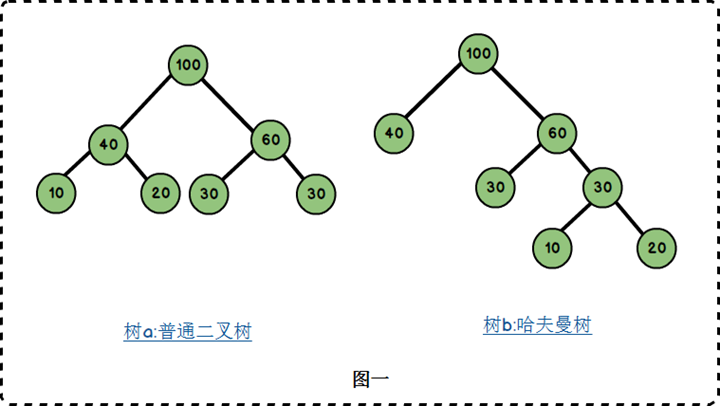
- 路径与路径长度:从树中一个节点到另一个节点之间的分支构成了两个节点之间的路径,路径上的分支数目称作路径长度。若规定根节点位于第一层,则根节点到第 H 层的节点的路径长度为 H-1.如树 b:100 到 60 的路径长度为 1;100 到 30 的路径长度为 2;100 到 20 的路径长度为 3。
- 树的路径长度:从根节点到每一节点的路径长度之和。树 a 的路径长度为 1+1+2+2+2+2=10;树 b 的路径长度为 1+1+2+2+3+3=12.
- 节点的权:将树中的节点赋予一个某种含义的数值作为该节点的权值,该值称为节点的权;
- 带权路径长度:从根节点到某个节点之间的路径长度与该节点的权的乘积。例如树 b 中,节点 10 的路径长度为 3,它的带权路径长度为 10*3=30;
- 树的带权路径长度:树的带权路径长度为所有叶子节点的带权路径长度之和,称为 WPL。树 a 的 WPL=2*(10+20+30+40)=200;树 b 的 WPL=1×40+2×30+3×10+3×20=190.而哈夫曼树就是树的带权路径最小的二叉树。
通信与信息熵
香农第二定律,即香农公式,描述了一个信道中的极限信息传输率和该信道能力,这是现代通信行业的“金科玉律”。香农提出的信息熵,解决了电报、电话、无线电等如何计量信号信息量的问题。但怎么在远距离通信中进一步提高信道容量?也就是信息传送速率上限,即“香农极限”。香农给出了信道容量公式,这使得至今几乎所有的现代通信理论都是基于这个公式展开。其数学表达式为:
$$C=B\log_2(1+\frac{S}{N})$$
其中:C 为信息速率的极限值;B 为信道带宽(Hz);S 为信号功率(W);N 为噪声功率(W);S/N 表示信噪比。
我们可以简单地把信息通道看作是城市道路,那么在这条道路上的单位时间内的车流量就受到道路宽度和车辆速度等因素的制约,在这些特定制约条件下,单位时间内最大车流量就被称为极限值。而根据香农定理,由于受到一些固有规律的制约,任何信道都不能无限增加信息传送的速率。从香农公式中我们可以看出,想要提高信息的传送速率关键在于提高信噪比和带宽。同时,C 一定时,B 与 S/N 可以互换,即带宽和信噪比可以互相交换,也就是说,在传输速度不变的情况下,提高带宽可以容忍更低的信噪比,反之亦然。
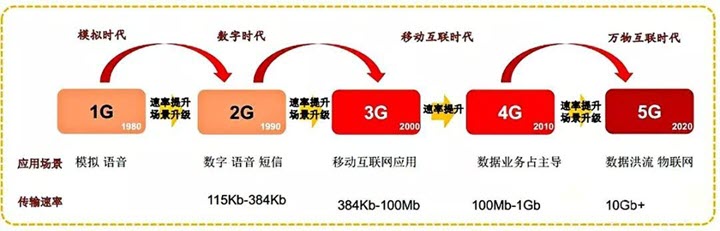
从 1G 至 2G 至 3G 至 4G,甚至到 5G 的通信变更,全世界一流的通信运营商和生厂商也一直废寝忘食地追逐着香农极限。在这期间,以香农公式为通信理论之基,通过不断革新技术,提高信噪比,增加带宽,我们也经历了大约每十年就发生一场时代剧变的移动通信技术演进史,生活也因此而瞬息万变。
华为 5G 与极化码
极化码(英语:Polar code)是一种前向错误更正编码方式,用于讯号传输。构造的核心是通过信道极化(channel polarization)处理,在编码侧采用方法使各个子信道呈现出不同的可靠性,当码长持续增加时,部分信道将趋向于容量近于1的完美信道(无误码),另一部分信道趋向于容量接近于0的纯噪声信道,选择在容量接近于1的信道上直接传输信息以逼近信道容量,是首个被证明能够达到香农极限的方法。
在解码侧,极化后的信道可用简单的逐次干扰抵消解码的方法,以较低的复杂度获得与最大似然解码相近的性能。
2008年在国际信息论ISIT会议上,土耳其毕尔肯大学埃达尔·阿利坎(Erdal Arıkan)教授首次提出了这个信道极化的概念,基于该理论,他给出了人类已知的第一种能够被严格证明达到信道容量的信道编码方法,并命名为极化码。
华为2016宣布4月份率先完成中国IMT-2020(5G)推进组第一阶段的空口关键技术验证测试,在5G信道编码领域全部使用极化码,2016年11月17日国际无线标准化机构3GPP第87次会议在美国拉斯维加斯召开,中国华为主推PolarCode(极化码)方案,美国高通主推低密度奇偶检查码(LDPC)方案,法国主推Turbo2.0方案,最终控制信道采用极化码,数据信道采用LDPC。
信息熵在机器学习的应用
信息增益
在决策树算法的学习过程中,信息增益是特征选择的一个重要指标,它定义为一个特征能够为分类系统带来多少信息,带来的信息越多,说明该特征越重要,相应的信息增益也就越大。
计算公式:infoGain = baseEntropy – EntropyAfter
- 当infoGain>0,表明集合信息熵减小,包含的信息更纯更有序,价值得到提高。
- 当infoGain<0,信息变得混沌。
- 当infoGain=0,信息量没有变化,但不表明信息没有变化。
我们要依据样本特征来分割数据集以使数据变得更加有序的过程就是要求一个使得infoGain>0的分类特征,而且是在所有的特征中使得infoGain值最大的特征。在决策树分类中,数据集包含的分类特征不止一个,那么,在第一次划分数据集时如何从整个特征集中抽出一个特征?信息增益便是对这种划分数据集前后信息是更有序了,还是更混乱的度量。选出取得信息增益最大的特征,以该特征对数据集分类,如果该特征共有n个特征值,那么划分数据集后会生成n个节点。这些n个节点再计算信息增益,并选出最大的特征,以此往复,直到最终节点仅包含同一类数据为止。
条件熵
在决策树的切分里,事件$x_i$可以认为是在样本中出现某个标签/决策。于是$P(x_i)$可以用所有样本中某个标签出现的频率来代替。但我们求熵是为了决定采用哪一个维度进行切分,因此有一个新的概念条件熵:
$$H(X|Y)=\sum_{y\in Y}{p(y)H(X|Y=y)}$$
这里我们认为Y就是用某个维度进行切分,那么y就是切成的某个子集合于是H(X|Y=y)就是这个子集的熵。因此可以认为就条件熵是每个子集合的熵的一个加权平均/期望。
信息增益
信息熵表示的是不确定度。均匀分布时,不确定度最大,此时熵就最大。当选择某个特征对数据集进行分类时,分类后的数据集信息熵会比分类前的小,其差值表示为信息增益。信息增益(Kullback-Leibler divergence)用于度量属性A对降低样本集合X熵的贡献大小。信息增益可以衡量某个特征对分类结果的影响大小。信息增益越大,越适用对X进行分析。
有了信息熵的定义后,信息增益的概念便很好理解了,表示分类后,数据整体信息熵的差值。我们假设特征集中有一个离散特征a,它有V个可能的取值${a^1,a^2,…,a^V}$,如果使用特征$a$来对样本$D$进行划分,那么会产$V$个分支节点,其中第$v$个分支节点中包含的样本集。我们记为$D^v$。于是,可计算出特征$a$对样本集$D$进行划分所获得的信息增益为:
$$Gain(D,a)=H(D)-H(D|a)=H(D)-\sum_{v=1}^{V}\frac{\left|D^v \right|}{\left|D \right|}H(D^v)$$
其实特征a对样本集D进行划分所获得的信息增益即为样本集D的信息熵减去经过划分后各个分支的信息熵之和。由于每个分支节点,所包含的样本数不同,所有在计算每个分支的信息熵时,需要乘上对应权重$\frac{\left|D^v \right|}{\left|D \right|}$,即样本数越多的分支节点对应的影响越大。
信息增益率
以信息增益值的大小为标准存在一定的问题,主要表现为类别之多的输入变量比类别值少的输入变量有更多的机会称为当前最佳分组变量。为了解决这个问题,不仅考虑信息增益的大小程度,还兼顾考虑为获得信息增益所付出的“代价”。
同样假设有数据集D,以及特征a,它有个可能的取值${a^1,a^2,…,a^V}$,如果数据集D在以特征a作为划分特征时,增益率定义为:
$$Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}$$
其中:
$$IV(a)=-\sum_{V}^{v=1}\frac{\left|D^v\right|}{\left|D \right|}\log2\frac{\left|D^v\right|}{\left|D \right|}$$
我们来看下上述增益率公式,其实$IV(a)$就是特征a本身的信息熵,也就说对应根据特征a的可能取值,所对应求得的信息熵,特征a的对应种类越多,也就是说越大,则的值通常会越大,从而增益率越小。这样,就可以避免信息增益中对可取数目比较多的特征有所偏好的缺点。然而增益率又会对取值数目较少的属性有偏好,因此又有一个“启发式”的规则:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
基尼指数
基尼指数跟信息熵的概念是一样的都是描述混乱的程度。基尼指数Gini(D)表示的是集合D的不确定性,基尼指数Gini(D,A)表示数据集D经过特征A划分以后集合D的不确定性,基尼指数越大说明我们集合的不确定性就越大,所以思想基本上和信息熵的概念是一致的。
给定样本集D,假设有K个类,样本点属于第k个类的概率为$p_k$,则概率分布的基尼指数定义为:
$$Gini(D)=\sum_{k=1}^{K}p_k(1-p_k)=1-\sum_{k=1}^{K}p_k^2$$
根据基尼指数定义,可以得到样本集合D的基尼指数,其中$C_k$表示数据集D中属于第k类的样本子集。
$$Gini(D)=1-\sum_{k=1}^{K}(\frac{|C_k|}{D})^2$$
基尼值反映了从数据集中随机抽取两个样本,其类别标记不一致的概率,因此基尼值越小,则数据集纯度越高。
对属性a进行划分,则属性a的基尼指数定义为:
$$Gini\_index(D,a)=\sum\limits_{v=1}^V\frac{\left|D^v\right|}{\left|D\right|}Gini(D^v)$$
如果数据集D根据特征A在某一取值a上进行分割,得到D1,D2两部分后,那么在特征A下集合D的基尼系数:
$$Gini\_Gini(D,a)=\frac{D_1}{D}Gini(D_1)+\frac{D_2}{D}Gini(D_2)$$
于是,我们在候选属性集合A中,选择哪个使得划分后基尼指数最小的属性作为最优划分属性,即:
$$a_*=\arg\limits_{a\in A}\min Gini\_index(D,a)$$
其中算法的停止条件有:
- 节点中的样本个数小于预定阈值,
- 样本集的Gini系数小于预定阈值(此时样本基本属于同一类),
- 或没有更多特征。
在ID3算法中我们使用了信息增益来选择特征,信息增益大的优先选择。在C4.5算法中,采用了信息增益比来选择特征,以减少信息增益容易选择特征值多的特征的问题。但是无论是ID3还是C4.5,都是基于信息论的熵模型的,这里面会涉及大量的对数运算。能不能简化模型同时也不至于完全丢失熵模型的优点呢?有!CART分类树算法使用基尼系数来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益(比)是相反的。
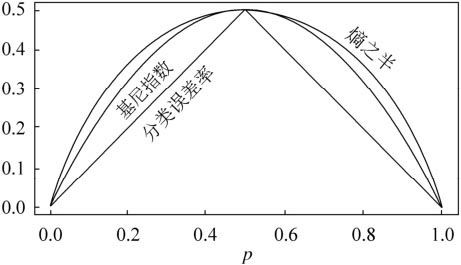 从上图可以看出,基尼系数和熵之半的曲线非常接近,仅仅在45度角附近误差稍大。因此,基尼系数可以做为熵模型的一个近似替代。而CART分类树算法就是使用的基尼系数来选择决策树的特征。同时,为了进一步简化,CART分类树算法每次仅仅对某个特征的值进行二分,而不是多分,这样CART分类树算法建立起来的是二叉树,而不是多叉树。这样一可以进一步简化基尼系数的计算,二可以建立一个更加优雅的二叉树模型。
从上图可以看出,基尼系数和熵之半的曲线非常接近,仅仅在45度角附近误差稍大。因此,基尼系数可以做为熵模型的一个近似替代。而CART分类树算法就是使用的基尼系数来选择决策树的特征。同时,为了进一步简化,CART分类树算法每次仅仅对某个特征的值进行二分,而不是多分,这样CART分类树算法建立起来的是二叉树,而不是多叉树。这样一可以进一步简化基尼系数的计算,二可以建立一个更加优雅的二叉树模型。
WOE与IV
在评分卡建模流程中,WOE(Weight of Evidence)常用于特征变换,IV(Information Value)则用来衡量特征的预测能力。
$$WOE_i=ln(\frac{Bad_i}{Bad_T}/\frac{Good_i}{Good_T})=ln(\frac{Bad_i}{Bad_T})-ln(\frac{Good_i}{Good_T})$$
IV(Information Value)是与WOE密切相关的一个指标,常用来评估变量的预测能力。因而可用来快速筛选变量。
IV的计算公式定义如下,其可认为是WOE的加权和:
$$IV_i=(\frac{Bad_i}{Bad_T}-\frac{Good_i}{Good_T})*WOE_i$$
$$IV=\sum_{i=1}^{n}IV_i$$
信息熵在营销场景的应用思考
在短信营销场景中,常常会遇到有些用户你给他发多少条促销短信他都无动于衷。针对这样的情况,通常我们会将这类用户称为营销不敏感用户。然而如何区分出这些用户会是一个挺头疼的问题,最常用的手段是通过营销反应次数的技术进行划分。比如定义营销5次都没有任何反馈的用户。以上定义存在的问题:
- 营销场景的不一致,导致有的营销转化高,有的营销转化低,不应等同看待
- 划分定义拍脑袋,针对某一个用户,营销5次没有反馈是从首次到第5次,还是5次计算可以间断,还是不需要从首次开始,只要连续5次都算。各种不同的定义无法说清楚那种更好。
假设我们把每次营销活动看成是信息反馈。针对某一个用户,假设我们期望控制营销的量,即针对营销不敏感用户进行剔除。假设我们定义:
- 营销成功,则获得的信息为:$H_s=-\log{R_{conversion}}$,其中$R_{conversion}$为营销计划的转化率
- 营销失败,则获得的信息为:$H_f=-\log{(1-R_{conversion})}$
假设按照上面的内容定义,针对每一次营销,营销成功与营销失败的用户可以获得的信息比为:$\frac{H_s}{H_f}=\frac{-\log{R_{conversion}}}{-\log{(1-R_{conversion})}}$
- 假设转化率为百分之2,则可提供的信息比为:$\frac{-\log\frac{2}{100}}{-\log\frac{98}{100}}\approx193.64$
- 假设转化率为千分之2,则可提供的信息比为:$\frac{-\log\frac{2}{1000}}{-\log\frac{998}{1000}}\approx3104.30$
显然,转化率越低,信息比其实越大。且差距非常的大。所以将用户对营销的敏感度定义为所有营销成功的信息量减去营销失败获得的信息量非常的不适合。
那么,接下来怎么办?能否以营销失败$H_f$进项评定?当营销成功只做参考:
$H(\theta)<H(F)=\sum_{i=1}^{n}H_{f_n}$
我们将不敏感度定义为过去一段时间营销失败获得信息和,如果营销成功,可将$H(F)$全部置零重新进行计算。
另外考虑到营销不成功还有可能是用户当下没有需求,所以可以让每次营销结果随着时间进行降权。比如:
$$H(\theta)<{H(F)}’=\sum_{i=1}^{n}(H_{f_n}\cdot0.99^{d_n})$$
其中$d_n$,为每次营销活动距离当前日期的天数。

这也太干货了,科普级
上面支付宝和微信打赏链接弄反啦哈哈。
感谢提醒~