什么是大数据杀熟?
大数据杀熟(Big Data Price Discrimination)是指企业利用用户的历史行为数据、消费习惯、设备信息、地理位置等个人隐私数据,通过算法分析对不同用户实施差异化定价的行为。其核心在于利用数据优势对用户进行“区别对待”,导致相同商品或服务在不同用户端显示不同价格,且通常对老用户、高频用户或高消费能力用户收取更高费用。

关键特征
- 数据驱动:
- 依赖大数据技术收集用户隐私(如浏览记录、购买频率、支付能力、设备型号等)。
- 通过机器学习模型预测用户的支付意愿(Price Sensitivity)。
- 隐蔽性:
- 价格差异不公开说明,用户难以察觉。
- 常伪装成“个性化推荐”“动态定价”等名义。
- 歧视性:
- 老用户价格 > 新用户价格(利用用户粘性)。
- 高消费用户价格 > 低消费用户价格(利用支付能力差异)。
常见场景
- 电商平台:
- 同一商品,老用户看到的价格高于新注册用户。
- 频繁浏览某商品的用户被推送更高价格。
- 出行服务:
- 同一行程,iPhone用户的车费高于安卓用户。
- 高频使用网约车的用户被收取更高费用。
- 会员体系:
- 付费会员实际购买价格反而高于非会员(利用会员的消费依赖性)。
争议焦点
- 伦理问题:
- 企业利用用户隐私数据谋利,违背“公平交易”原则。
- 高频用户或忠实用户被反向惩罚,损害消费者信任。
- 法律风险:
- 违反《个人信息保护法》:未经用户同意收集和使用隐私数据。
- 违反《反垄断法》:滥用市场支配地位实施价格歧视。
- 违反《消费者权益保护法》:侵犯知情权和公平交易权。
与“合理定价策略”的区别
并非所有差异化定价都是“杀熟”,以下情况通常合法合规:
- 动态定价:根据市场供需调整价格(如演唱会门票、机票淡旺季浮动)。
- 公开促销:对新用户发放首单优惠券,且规则透明。
- 成本差异化:因物流、地区成本导致的合理价格差异。
大数据杀熟的本质是技术滥用,通过算法将用户隐私转化为“定价优势”。其合法性取决于是否侵犯用户权益、是否透明公开规则。
为什么要规避大数据杀熟
在规避“大数据杀熟”的前提下进行价格弹性实验,核心目的是在合法合规、保护用户权益的基础上,科学探索市场对价格的敏感度,以实现企业商业目标与用户信任之间的平衡。
法律与伦理的必然要求
- 法律风险规避:直接利用用户隐私数据(如消费记录、设备信息、地理位置)进行差异化定价,可能违反《个人信息保护法》《反垄断法》《消费者权益保护法》等法规。例如:
- 中国《个人信息保护法》要求企业处理数据需获得用户明确同意,且不得滥用数据实施歧视性行为。
- 欧盟《通用数据保护条例》(GDPR)对“自动化决策”有严格限制,禁止算法对用户进行不公平对待。
- 伦理责任:价格弹性实验若涉及“杀熟”,会损害用户对企业的信任,尤其是老用户或高频用户可能因被“反向惩罚”而流失。例如:老用户发现同一商品价格高于新用户,可能认为企业“收割忠诚”,导致品牌声誉受损。
实验结果的科学性与可持续性
- 避免数据偏差:大数据杀熟依赖个体画像(如高消费用户画像),可能导致实验结论片面化。例如:针对高收入用户提价后转化率下降,可能仅反映特定群体敏感度,而非整体市场规律。
- 长期商业价值:通过公平实验得出的价格策略更具普适性,避免因短期投机行为(如收割特定用户)导致市场萎缩。例如:若发现某价格区间能覆盖80%用户的支付意愿,企业可通过规模效应提升整体利润,而非依赖对少数用户的高价策略。
用户隐私与数据安全的底线
- 最小化数据收集:规避大数据杀熟的实验设计(如随机分组、匿名化处理)能减少对用户隐私的依赖,降低数据泄露风险。例如:仅需收集用户是否购买、支付金额等脱敏数据,而非关联到个人身份或行为历史。
- 符合监管趋势:全球监管机构对算法歧视和数据滥用的审查趋严,合规实验能避免高额罚款或业务受限。
价格弹性实验的合理目标
价格弹性实验的本质是研究市场对价格的宏观反应,而非针对个体“榨取价值”。合理目标包括:
- 群体支付意愿分析:例如,测试某商品价格从100元降至90元时,整体销量增长是否覆盖利润损失。
- 供需关系优化:例如,在淡旺季调整价格,平衡库存与收益。
- 促销策略验证:例如,验证“满100减20”是否比“直接8折”更能刺激消费。
对比:大数据杀熟 vs. 合规价格弹性实验
| 维度 | 大数据杀熟 | 合规价格弹性实验 |
| 数据基础 | 依赖用户隐私数据(如消费记录、设备信息) | 基于匿名化或群体数据(如随机分组) |
| 定价逻辑 | 针对个体画像差异化定价 | 基于公开因素(时间、地区、产品版本)调整价格 |
| 用户感知 | 隐蔽、可能引发不信任 | 透明或可解释(如“限时折扣”“新用户优惠”) |
| 法律风险 | 高(违反隐私保护和反歧视法规) | 低(符合数据最小化和公平性原则) |
| 商业可持续性 | 短期收益高,长期损害用户忠诚度 | 短期收益可控,长期建立信任与市场稳定性 |
如何合规进行价格弹性实验?
合规要求用一句话表述:不同用户在相同条件在查询某件产品的价格是一致的。
方案一:时间片轮转(每日切换分组)
原理:将用户按时间段划分到不同实验组(如每日0-12点为A组,13-24点为B组,次日轮换)。
优点
- 避免个体数据污染:同一用户在不同时间段可能分属不同组,减少对单一用户的长期跟踪,降低“杀熟”风险。
- 简单易行:无需复杂分组逻辑,仅需按时间切换规则即可。
- 消除用户特征干扰:时间段内所有用户随机分布,减少用户画像差异对结果的影响。
缺点
- 时间因素干扰:不同时间段用户行为差异较大(如白天购物多为办公场景,夜间为个人场景),可能混淆实验结果。
- 用户重复曝光问题:用户可能在多个时间段访问,导致数据交叉污染(如用户今天上午看到A价格,今晚看到B价格)。
- 实验周期长:需多次轮换周期(如一周)才能消除单日特殊事件(如节假日)的影响。
注意事项
- 控制时间变量:需记录节假日、促销活动等外部因素,避免与价格实验混淆。
- 用户去重统计:若用户多次访问,需明确统计规则(如仅首次访问有效)。
- 避免过短时间片:时间段划分不宜过短(如每小时切换),否则用户感知混乱。
方案二:按城市分组(固定城市分组)
原理:将产品所在不同城市(比如酒店)随机分为A/B组(如北京、上海为A组,广州、深圳为B组)。
优点
- 消除区域差异干扰:同一城市内特征相对一致,实验结果更易归因于价格变化。
- 便于长期观察:固定分组可长期追踪城市级数据(如复购率、留存率)。
- 避免跨城市用户干扰:用户通常在同一城市完成消费,减少跨组数据交叉。
缺点
- 城市间固有差异影响:不同城市的经济水平、竞争环境差异可能导致结果偏差。
- 样本量不均衡:若部分城市用户量过小(如三四线城市),统计结果可能不显著。
- 合规风险:若城市分组与用户敏感特征(如收入水平)强相关,可能被质疑变相“地域歧视”。
注意事项
- 随机分层抽样:按城市规模、经济水平分层后随机分组(如一线/二线/三线城市均衡分布)。
- 规避敏感标签:避免直接按“高消费城市”“低收入城市”等标签分组。
方案三:时间+城市混合分组(每日切换城市分组)
原理:今日A组城市在次日切换为B组,同时结合时间段轮换(如北京今日为A组,明日为B组)。
优点
- 双重随机化:时间与城市双重轮换,进一步减少地域和时间的系统性偏差。
- 降低长期地域歧视风险:城市分组不固定,避免某城市长期承受高价策略。
- 增强结果稳健性:通过多次轮换验证价格策略的普适性。
缺点
- 逻辑复杂度高:需同时管理城市分组和时间片切换,技术实现难度大。
- 用户感知混乱:同一用户在不同天看到不同价格,可能引发信任问题(如“为何昨天更便宜?”)。
- 数据拆分复杂:需按时间和城市双重维度拆分数据,分析成本较高。
注意事项
- 明确用户告知:若价格变动频繁,需提前说明规则(如“每日优惠不同”)。
- 自动化分组系统:依赖自动化工具确保分组切换准确(如避免城市分组与时间片错位)。
如何确认哪种方式更优秀?
验证逻辑:选择过去一段时间,未进行任何实验的数据,模拟实验分组,计算不同实验组下的分组差异,确定波动收敛时间。
时间片轮组的模拟实验
import pandas as pd
# 假设数据已经加载到一个DataFrame中
data = pd.read_csv('data/ABTest.csv')
# 将日期列转换为datetime格式
data['Date'] = pd.to_datetime(data['Date'])
# 定义实验开始日期和持续时间
start_dates = pd.date_range(start='2025-02-13', end='2025-02-23', freq='D')
duration_days = range(1, 15)
# 定义A/B分组
def get_group(date, day_offset):
if (day_offset % 2) == 0:
return {'0~11': 'A', '12~23': 'B'}
else:
return {'0~11': 'B', '12~23': 'A'}
# 初始化结果存储
results = []
# 遍历每个实验开始日期和持续时间
for start_date in start_dates:
for duration in duration_days:
# 初始化A/B组的统计量
group_stats = {'A': {'UV': 0, 'Order': 0}, 'B': {'UV': 0, 'Order': 0}}
# 遍历实验期间的每一天
for day_offset in range(duration):
current_date = start_date + pd.Timedelta(days=day_offset)
group_assignment = get_group(current_date, day_offset)
# 过滤当天的数据
daily_data = data[data['Date'] == current_date]
# 分配数据到A/B组
for _, row in daily_data.iterrows():
group = group_assignment[row['TimeQuantum']]
group_stats[group]['UV'] += row['UV']
group_stats[group]['Order'] += row['Order']
# 计算均UV订单量
uv_order_A = group_stats['A']['Order'] / group_stats['A']['UV'] if group_stats['A']['UV'] != 0 else 0
uv_order_B = group_stats['B']['Order'] / group_stats['B']['UV'] if group_stats['B']['UV'] != 0 else 0
# 计算均UV订单量差值和波动率
uv_order_diff = uv_order_A - uv_order_B
uv_order_volatility = uv_order_diff / min(uv_order_A, uv_order_B) if min(uv_order_A, uv_order_B) != 0 else 0
# 存储结果
results.append({
'实验开始日期': start_date,
'持续时间': duration,
'A组总UV': group_stats['A']['UV'],
'A组总Order': group_stats['A']['Order'],
'B组总UV': group_stats['B']['UV'],
'B组总Order': group_stats['B']['Order'],
'A组均UV订单量': uv_order_A,
'B组均UV订单量': uv_order_B,
'均UV订单量差值': uv_order_diff,
'波动率': uv_order_volatility,
})
results_df = pd.DataFrame(results)
print(results_df.head())
数据可视化呈现
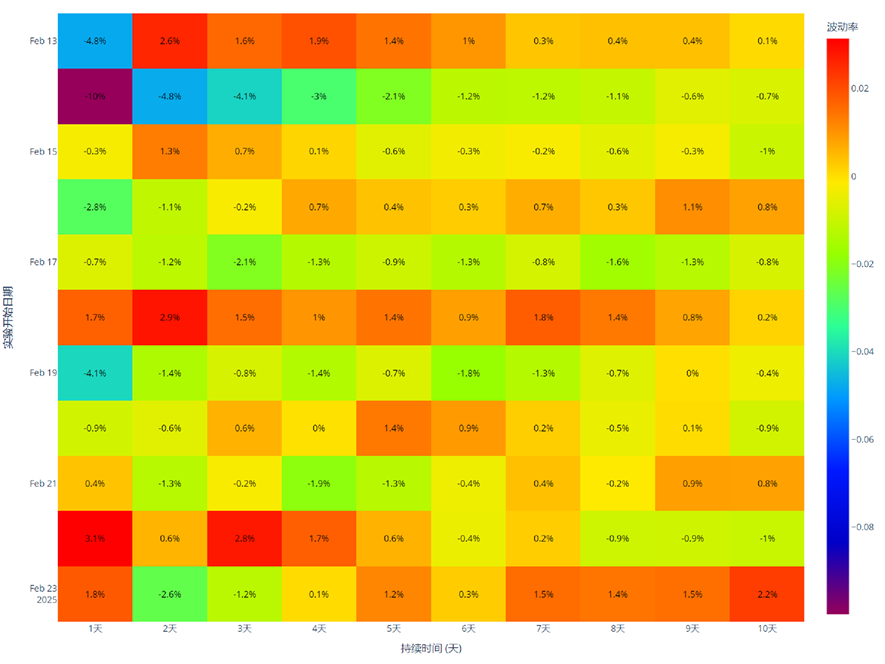
热力图呈现:
import plotly.express as px
heatmap_data = results_df[['实验开始日期', '持续时间', '波动率']]
# 将日期转换为字符串格式,方便显示
heatmap_data['实验开始日期'] = heatmap_data['实验开始日期'].dt.strftime('%Y-%m-%d')
# 将波动率转换为百分数,并保留一位小数
heatmap_data['波动率百分数'] = (heatmap_data['波动率'] * 100).round(1)
# 使用 plotly 绘制热力图
fig = px.imshow(
heatmap_data.pivot(index='实验开始日期', columns='持续时间', values='波动率'),
labels=dict(x="持续时间 (天)", y="实验开始日期", color="波动率"),
x=[f"{i}天" for i in range(1, 11)], # X 轴标签
y=heatmap_data['实验开始日期'].unique(), # Y 轴标签
color_continuous_scale='Rainbow', # 更换颜色主题为 Rainbow
title="波动率热力图 (按实验开始日期和持续时间)"
)
# 在每个方格内显示百分数形式的波动率数值
fig.update_traces(
text=heatmap_data.pivot(index='实验开始日期', columns='持续时间', values='波动率百分数'), # 显示的文本
texttemplate="%{text}%", # 格式化文本为百分数
textfont={"size": 12, "color": "black"} # 设置文本字体大小和颜色
)
fig.update_layout(
width=1200, # 设置图形宽度
height=1000, # 设置图形高度
xaxis_title="持续时间 (天)",
yaxis_title="实验开始日期",
coloraxis_colorbar=dict(title="波动率")
)
fig.show()
波动区间可视化:
import plotly.graph_objects as go
import numpy as np
# 数据预处理
clean_df = results_df[(results_df['波动率'].notna()) & np.isfinite(results_df['波动率'])].copy()
# 按实验天数计算统计量
stats_df = clean_df.groupby('持续时间').agg(
mean_vol=('波动率', 'mean'),
std_vol=('波动率', 'std'),
count=('波动率', 'count')
).reset_index()
# 创建可视化图表
fig = go.Figure()
# 添加均值线
fig.add_trace(go.Scatter(
x=stats_df['持续时间'],
y=stats_df['mean_vol'],
mode='lines+markers',
name='均值',
line=dict(color='rgb(31, 119, 180)', width=2),
marker=dict(size=8, symbol='circle'),
hovertemplate='天数: %{x}<br>均值: %{y:.4f}<extra></extra>'
))
# 添加误差带(均值±标准差)
fig.add_trace(go.Scatter(
x=stats_df['持续时间'].tolist() + stats_df['持续时间'].tolist()[::-1], # 正序+倒序形成闭合区域
y=(stats_df['mean_vol'] + stats_df['std_vol']).tolist() +
(stats_df['mean_vol'] - stats_df['std_vol']).tolist()[::-1],
fill='toself',
fillcolor='rgba(31, 119, 180, 0.15)',
line=dict(color='rgba(255,255,255,0)'),
hoverinfo='skip',
name='标准差范围'
))
# 设置图表布局
fig.update_layout(
title={
'text': "不同实验天数的波动率变化(均值±标准差)",
'y': 0.9,
'x': 0.5,
'xanchor': 'center',
'yanchor': 'top'
},
xaxis=dict(
title='实验持续时间(天)',
dtick=1,
gridcolor='lightgray',
showgrid=True
),
yaxis=dict(
title='波动率',
gridcolor='lightgray',
showgrid=True
),
hovermode='x unified',
plot_bgcolor='white',
paper_bgcolor='white',
template='plotly_white',
height=600,
width=1000,
legend=dict(
orientation="h",
yanchor="bottom",
y=1.02,
xanchor="right",
x=1
)
)
# 添加辅助标注
fig.add_annotation(
xref='paper',
yref='paper',
x=0.05,
y=0.95,
text=f"总实验次数: {len(clean_df)}",
showarrow=False,
font=dict(size=12)
)
# 显示图表
fig.show()
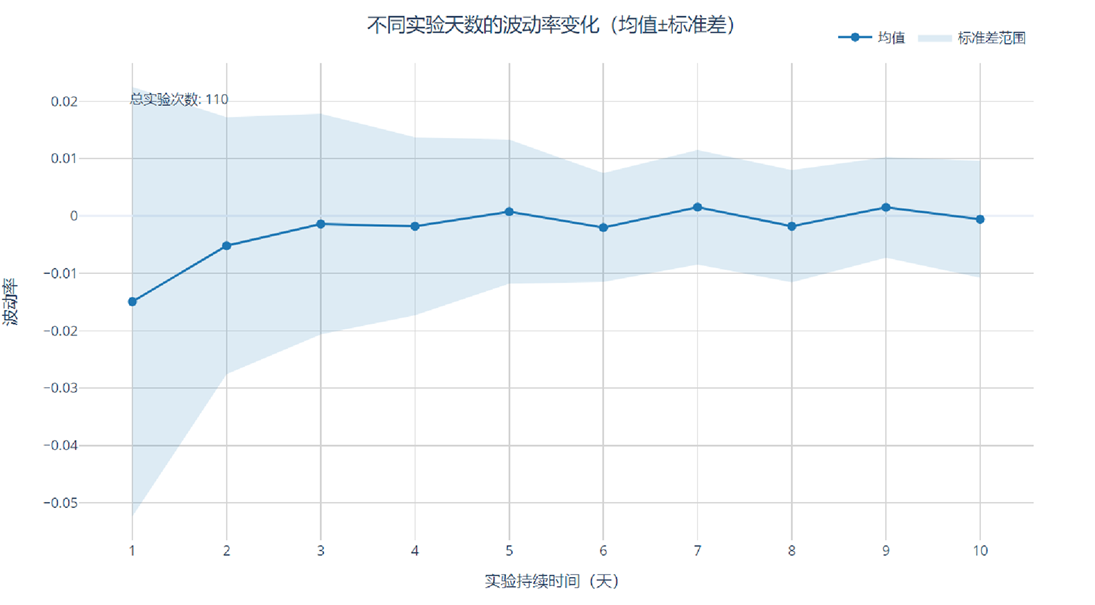
数据结论
- 时间切片轮替:数据是10天收敛,误差范围[-1%,2%],均值>0
- 日期切片轮替:数据是10天收敛,误差范围[-2%,1%],均值<0
- 随机城市轮替:数据偏向一方,无法收敛
- 指定城市轮替:数据偏向一方,无法收敛
- 日期+随机城市轮替:数据是10天收敛,误差范围[-1%,1%],均值=0
- 日期+指定城市轮替:数据是6天收敛,误差范围[-1%,1%],均值=0
实验分析下来:日期+指定城市轮替效果最佳,收敛速度最快,误差范围在1%。
指定城市分组方法
按照贪心法划分城市:
- 数据准备:首先将数据按城市进行汇总,计算每个城市的总UV、单量和营收等。
- 贪心算法:按UV从大到小排序,依次将城市分配到A组或B组,每次分配时计算将城市加入A组或B组后的偏差,选择偏差较小的分组。
- 输出结果:最终输出A组和B组的城市列表,以及每组的UV、订单量和营收。
import pandas as pd
df = pd.read_csv("data/ABTest.csv")
# 计算每个城市的总UV、总订单量、总营收
city_stats = df.groupby('City').agg({'UV': 'sum', 'Order': 'sum', 'Revenue': 'sum'}).reset_index()
# 初始化A组和B组
group_A = []
group_B = []
# 初始化A组和B组的总UV、总订单量、总营收
total_UV_A, total_UV_B = 0, 0
total_orders_A, total_orders_B = 0, 0
total_revenue_A, total_revenue_B = 0, 0
# 按UV从大到小排序
city_stats = city_stats.sort_values(by='UV', ascending=False)
# 贪心算法分配城市到A组或B组
for index, row in city_stats.iterrows():
city = row['City']
uv = row['UV']
orders = row['Order']
revenue = row['Revenue']
# 计算将当前城市加入A组或B组后的偏差
uv_A = total_UV_A + uv
uv_B = total_UV_B
orders_A = total_orders_A + orders
orders_B = total_orders_B
revenue_A = total_revenue_A + revenue
revenue_B = total_revenue_B
# 计算偏差
uv_deviation_A = abs(uv_A - uv_B) / (uv_A + uv_B)
orders_deviation_A = abs(orders_A - orders_B) / (orders_A + orders_B)
revenue_deviation_A = abs(revenue_A - revenue_B) / (revenue_A + revenue_B)
# 计算将当前城市加入B组后的偏差
uv_A = total_UV_A
uv_B = total_UV_B + uv
orders_A = total_orders_A
orders_B = total_orders_B + orders
revenue_A = total_revenue_A
revenue_B = total_revenue_B + revenue
uv_deviation_B = abs(uv_A - uv_B) / (uv_A + uv_B)
orders_deviation_B = abs(orders_A - orders_B) / (orders_A + orders_B)
revenue_deviation_B = abs(revenue_A - revenue_B) / (revenue_A + revenue_B)
# 选择偏差较小的分组
if max(uv_deviation_A, orders_deviation_A, revenue_deviation_A) < max(uv_deviation_B, orders_deviation_B, revenue_deviation_B):
group_A.append(city)
total_UV_A += uv
total_orders_A += orders
total_revenue_A += revenue
else:
group_B.append(city)
total_UV_B += uv
total_orders_B += orders
total_revenue_B += revenue
# 输出结果
print("A组城市:", group_A)
print("B组城市:", group_B)
print("A组总UV:", total_UV_A, "B组总UV:", total_UV_B)
print("A组总订单量:", total_orders_A, "B组总订单量:", total_orders_B)
print("A组总营收:", total_revenue_A, "B组总营收:", total_revenue_B)