Python标准库学习之堆heapq

heapq 模块是 Python 标准库中的一个模块，提供了用于操作堆（即优先队列）的函数。堆是一种特殊的树状数据结构，其中每个父节点的值都小于或等于其子节点的值（最小堆），或者每个父节点的值都大于或等于其子节点的值（最大堆）。heapq 模块默认实现的是最小堆，但它提供了一些工具，可以用来实现最大堆等其他堆类型。

什么是堆？

堆（Heap）是一种特殊的树形数据结构，满足以下特性：

完全二叉树：堆是一棵完全二叉树。这意味着所有层（除了最后一层）都是满的，并且最后一层的所有节点都尽可能地靠左。

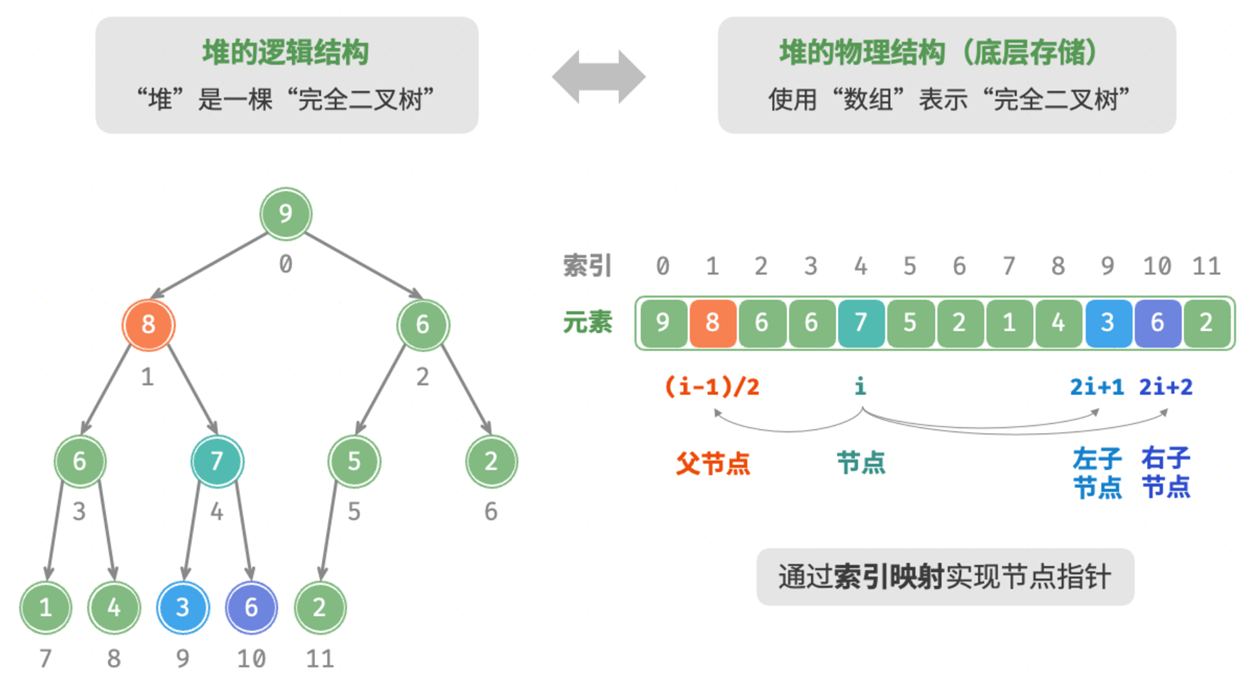
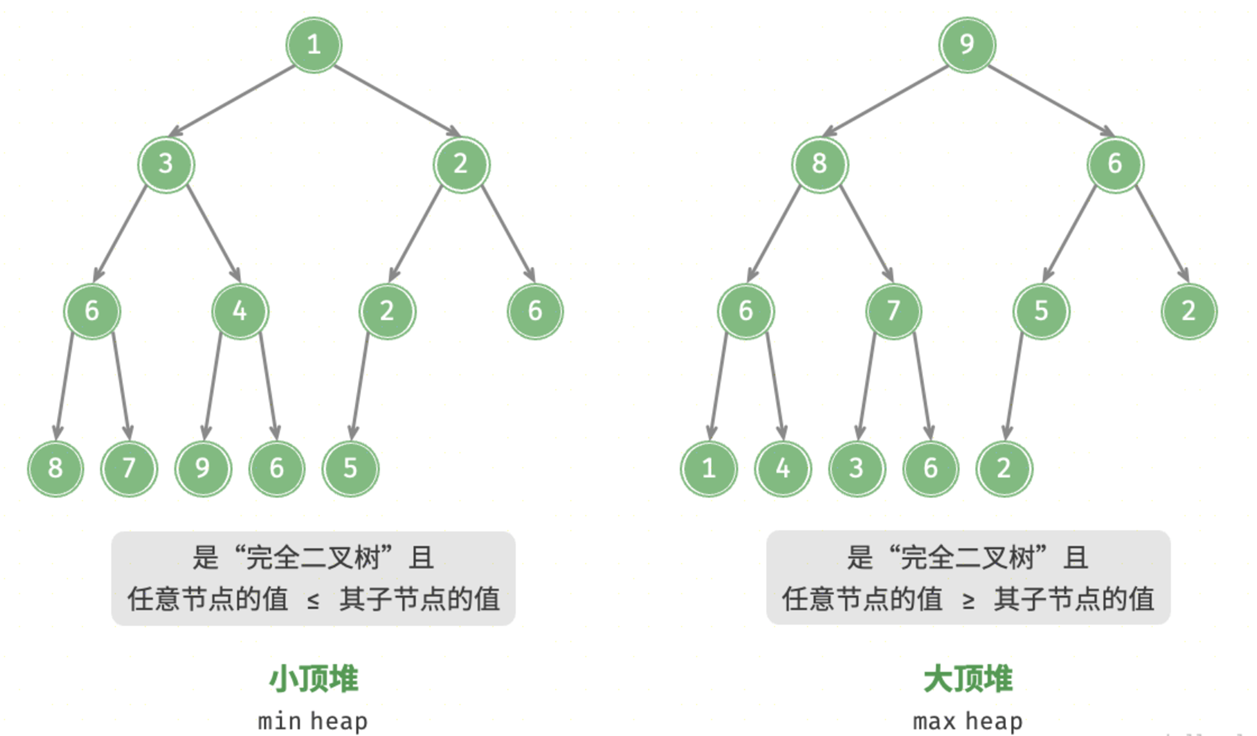
堆性质：
- 最大堆（Max Heap）：对于最大堆，每个节点的值都大于或等于其子节点的值。换句话说，堆顶（根节点）是整个堆中最大的元素。
- 最小堆（Min Heap）：对于最小堆，每个节点的值都小于或等于其子节点的值。因此，堆顶是整个堆中最小的元素。

操作

以下是堆的一些基本操作：

插入元素：将新元素插入堆中，并保持堆的性质。
删除堆顶元素：移除堆顶元素，并重建堆以保持其性质。
构建堆：将一个无序的数组构建成堆结构。
堆化（Heapify）：调整一个子树，使其满足堆的性质。

数据结构、堆和优先级队列

堆是具体的数据结构，而优先级队列是抽象的数据结构。抽象数据结构确定接口，而具体数据结构定义实现。堆通常用于实现优先级队列。它们是实现 priority queue abstract data structure 的最流行的具体数据结构。

抽象数据结构指定操作及其之间的关系。例如，priority queue abstract 数据结构支持三种操作：

is_empty检查队列是否为空。
add_element将元素添加到队列中。
pop_element会弹出优先级最高的元素。

优先级队列通常用于优化任务执行，其中的目标是处理优先级最高的任务。任务完成后，其优先级会降低，并返回到队列中。

确定元素的优先级有两种不同的约定：

最大的元素具有最高优先级。
最小的元素具有最高优先级。

这两个约定是等效的，因为您始终可以反转有效顺序。例如，如果你的元素由数字组成，那么使用负数会颠倒约定。

Python 模块使用第二种约定，这通常是两者中更常见的一种。在此约定下，最小的元素具有最高优先级。这听起来可能令人惊讶，但它通常非常有用。

优先级队列的用途

优先级队列是一种重要的数据结构，它允许在数据元素中指定优先级，并且始终按照优先级的顺序处理这些元素。优先级队列的用途广泛，以下是一些常见的应用场景：

任务调度：在操作系统中，优先级队列用于调度任务或进程。任务根据其优先级被安排执行，确保关键任务可以得到优先处理。
路径搜索算法：在图算法中，优先级队列被用于实现Dijkstra算法和A*算法。这些算法用于找到图中节点之间的最短路径。优先级队列帮助有效地选择下一个要扩展的节点。
事件驱动仿真：在离散事件仿真中，事件根据发生的时间被放入优先级队列中。仿真系统通过按时间顺序处理事件来模拟系统的行为。
数据流处理：在实时数据流处理中，优先级队列可以用于管理和处理高优先级的数据流，确保重要的数据得到及时处理。
内存管理：在垃圾回收算法中，优先级队列可用于管理内存块的回收优先级，帮助优化内存分配和回收。
网络通信：在网络路由中，数据包可以根据其优先级被放入优先级队列，以确保高优先级的数据包能够快速传输。
负载均衡：在服务器负载均衡中，优先级队列可用于管理请求的优先级，确保关键请求得到快速响应。
搜索引擎：在搜索引擎中，优先级队列用于管理待处理的网页或查询请求，根据优先级对资源进行调度。
人工智能和游戏开发：在AI和游戏开发中，优先级队列用于管理游戏事件、AI决策树的节点扩展等。
消息传递系统：在消息队列系统中，优先级队列可以用于按优先级顺序处理消息，确保关键消息得到优先传递。

Python中的堆heapq

heapq是Python标准库中的一个模块，提供了堆队列算法，也称为优先级队列算法。这个模块实现的是最小堆（min-heap），这意味着堆顶元素总是当前堆中最小的元素。以下是heapq模块的一些常用功能和使用示例：

常用功能

heappush(heap, item)：
- 将元素item压入堆中。
- 例子：heappush(heap, 3)
heappop(heap)：
- 弹出并返回堆中的最小元素。
- 例子：smallest = heapq.heappop(heap)
heappushpop(heap, item)：
- 将item压入堆中，然后弹出并返回堆中的最小元素。
- 例子：smallest = heapq.heappushpop(heap, 3)
heapreplace(heap, item)：
- 弹出并返回堆中的最小元素，然后将item压入堆中。
- 例子：smallest = heapq.heapreplace(heap, 3)
heapify(x)：
- 将列表x转化为堆，原地进行，时间复杂度为O(n)。
- 例子：heapify(x)
nlargest(n, iterable, key=None)：
- 返回可迭代对象iterable中最大的n个元素。
- 例子：largest_three = heapq.nlargest(3, iterable)
nsmallest(n, iterable, key=None)：
- 返回可迭代对象iterable中最小的n个元素。
- 例子：smallest_three = heapq.nsmallest(3, iterable)

使用示例

import heapq

# 创建一个空的最小堆
min_heap = []

# 向堆中添加元素
heapq.heappush(min_heap, 5)
heapq.heappush(min_heap, 3)
heapq.heappush(min_heap, 8)
heapq.heappush(min_heap, 1)

# 弹出并返回最小元素
print(heapq.heappop(min_heap))  # 输出: 1

# 查看当前堆的状态
print(min_heap)  # 输出: [3, 5, 8]

# 将列表转化为堆
data = [9, 6, 2, 7, 4]
heapq.heapify(data)
print(data)  # 输出: [2, 4, 6, 7, 9]

# 找到列表中最大的三个元素
largest_three = heapq.nlargest(3, data)
print(largest_three)  # 输出: [9, 7, 6]

# 找到列表中最小的三个元素
smallest_three = heapq.nsmallest(3, data)
print(smallest_three)  # 输出: [2, 4, 6]

注意事项

heapq模块实现的是最小堆，因此如果需要实现最大堆，可以将元素取负数来进行处理。
heapq是基于列表实现的，因此在使用时需要传入一个列表作为堆的容器。
操作的时间复杂度通常是O(log n)（如heappush和heappop），而构建堆的时间复杂度为O(n)（如heapify）。

实现最大堆

heapq模块在Python中实现的是最小堆（min-heap），这意味着堆顶元素总是当前堆中最小的元素。如果你需要实现最大堆（max-heap），可以通过对元素进行适当的变换来模拟最大堆的行为。具体来说，你可以将元素的值取负数，从而在逻辑上反转大小关系。以下是如何使用heapq实现最大堆的方法：

在将元素插入堆时，存储元素的负值。
在从堆中弹出元素时，再将负值转回正值。

import heapq

# 创建一个空的最大堆
max_heap = []

# 向堆中添加元素（取负数）
heapq.heappush(max_heap, -5)
heapq.heappush(max_heap, -3)
heapq.heappush(max_heap, -8)
heapq.heappush(max_heap, -1)

# 弹出并返回最大元素（注意取反）
max_value = -heapq.heappop(max_heap)
print(max_value)  # 输出: 8

# 查看当前最大堆的状态（注意取反）
current_max = -max_heap[0]
print(current_max)  # 输出: 5

# 找到列表中最大的三个元素
data = [9, 6, 2, 7, 4]
max_heap = [-x for x in data]
heapq.heapify(max_heap)
largest_three = [-heapq.heappop(max_heap) for _ in range(3)]
print(largest_three)  # 输出: [9, 7, 6]

注意事项

元素取反：由于heapq是基于最小堆的实现，为了模拟最大堆，需要在插入和弹出元素时对元素进行取反操作。
代码可读性：虽然这种方法有效，但对元素取反可能会影响代码的可读性，尤其是在复杂的应用中。
性能：取反操作对性能影响较小，但在某些性能敏感的场景中，可能需要考虑其他数据结构（如自定义实现的最大堆）。

参考链接：

Python标准库学习之堆heapq