Python异常检测包：PyOD

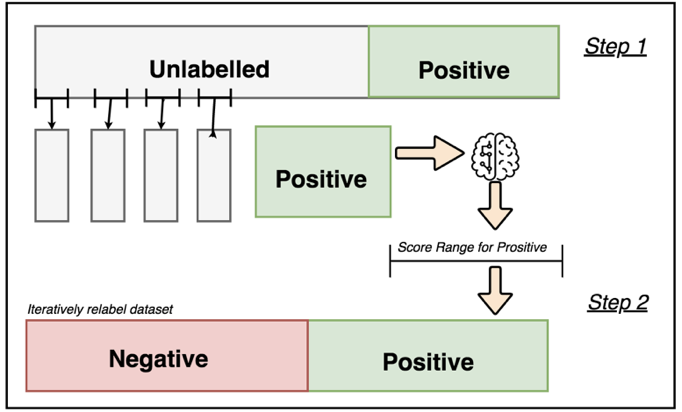
异常检测(anomaly detection)，也叫异常分析(outlier analysis或者outlier detection)或者离群值检测，在工业上有非常广泛的应用场景：

金融业：从海量数据中找到“欺诈案例”，如信用卡反诈骗，识别虚假信贷
网络安全：从流量数据中找到“侵入者”，识别新的网络入侵模式
在线零售：从交易数据中发现“恶意买家”，比如恶意刷评等
生物基因：从生物数据中检测“病变”或“突变”

同时它可以被用于机器学习任务中的预处理（preprocessing），防止因为少量异常点存在而导致的训练或预测失败。换句话来说，异常检测就是从茫茫数据中找到那些“长得不一样”的数据。但检测异常过程一般都比较复杂，而且实际情况下数据一般都没有标签(label)，我们并不知道哪些数据是异常点，所以一般很难直接用简单的监督学习。异常值检测还有很多困难，如极端的类别不平衡、多样的异常表达形式、复杂的异常原因分析等。

异常值不一定是坏事。例如，如果在生物学中实验，一只老鼠没有死，而其他一切都死，那么理解为什么会非常有趣。这可能会带来新的科学发现。因此，检测异常值非常重要。

PyOD简介

PyOD（Python Outlier Detection）是一个用于检测异常值（outliers）的开源Python库。它专注于提供多种异常检测算法，适用于不同类型的数据集和应用场景。

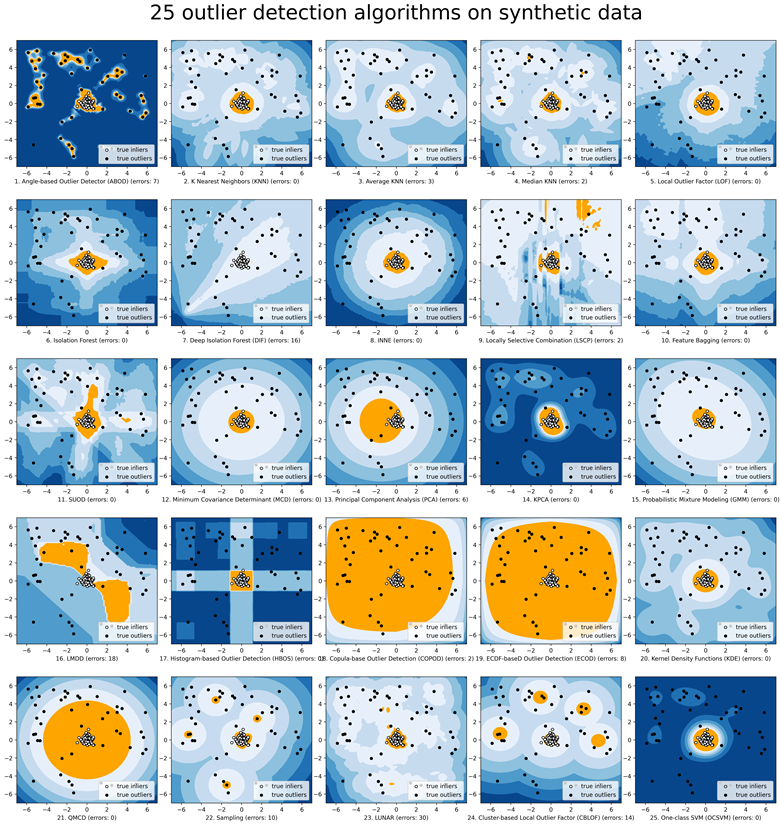
PyOD作为一个专门用于异常检测的Python库，具有以下主要优点：

多样的算法选择。PyOD提供了多种异常检测算法，涵盖线性模型、概率模型、聚类模型、邻域模型、神经网络模型和集成模型。这种多样性允许用户根据数据特性和具体需求选择最合适的算法。
易于使用。PyOD的设计简洁，API与scikit-learn类似，因此对于有scikit-learn经验的用户来说，上手非常容易。用户可以通过简单的代码来加载数据、训练模型和检测异常。
良好的兼容性。PyOD与NumPy、SciPy、scikit-learn等其他流行的Python库兼容。它还可以与Pandas无缝结合，使得数据处理更加方便。
可视化工具。PyOD提供了一些基本的可视化工具，帮助用户理解模型的性能和数据的异常分布。这对于调试和优化模型非常有帮助。
支持大规模数据。许多PyOD中的算法能够有效处理大规模数据集，适用于实际应用中的大数据场景。
开放源码和社区支持。作为一个开源项目，PyOD在GitHub上有活跃的社区支持，用户可以获取帮助、报告问题和贡献代码。这种开放性促进了库的不断改进和更新。
文档齐全。PyOD有详细的文档和教程，涵盖从基本使用到高级应用的各个方面，帮助用户快速掌握库的使用。
集成的模型选择和评估。PyOD内置了一些用于模型选择和性能评估的工具，比如交叉验证、异常检测的评估指标等，方便用户在不同模型间进行比较和选择。

这些优点使得PyOD成为异常检测任务中一个强大而灵活的工具，能够满足从学术研究到工业应用的多种需求。

PyOD的组成

PyOD工具包由四个主要功能组组成：

单独的检测算法

概率模型
- ECOD：使用经验累积分布函数的无监督异常检测，2022
- ABOD：基于角度的异常检测，2008
- FastABOD：使用近似的快速角度异常检测，2008
- COPOD：基于Copula的异常检测，2020
- MAD：中位数绝对偏差（MAD），1993
- SOS：随机异常选择，2012
- QMCD：准蒙特卡罗差异异常检测，2001
- KDE：使用核密度函数的异常检测，2007
- Sampling：通过采样的快速基于距离的异常检测，2013
- GMM：用于异常分析的概率混合建模
线性模型
- PCA：主成分分析（到特征向量超平面的加权投影距离之和），2003
- KPCA：核主成分分析，2007
- MCD：最小协方差行列式（使用马氏距离作为异常分数），1999
- CD：使用库克距离进行异常检测，1977
- OCSVM：单类支持向量机，2001
- LMDD：基于偏差的异常检测（LMDD），1996
邻域模型
- LOF：局部异常因子，2000
- COF：基于连通性的异常因子，2002
- (增量) COF：内存高效的基于连通性的异常因子（速度较慢但降低存储复杂度），2002
- CBLOF：基于聚类的局部异常因子，2003
- LOCI：使用局部相关积分的快速异常检测，2003
- HBOS：基于直方图的异常分数，2012
- kNN：k近邻（使用到第k个最近邻的距离作为异常分数），2000
- AvgKNN：平均k近邻（使用到k个最近邻的平均距离作为异常分数），2002
- MedKNN：中位k近邻（使用到k个最近邻的中位距离作为异常分数），2002
- SOD：子空间异常检测，2009
- ROD：基于旋转的异常检测，2020
异常集成
- IForest：孤立森林，2008
- INNE：使用最近邻集成的孤立异常检测，2018
- DIF：用于异常检测的深度孤立森林，2023
- FB：特征装袋，2005
- LSCP：局部选择并行异常集成的组合，2019
- XGBOD：基于XGBoost的异常检测（有监督），2018
- LODA：轻量级在线异常检测器，2016
- SUOD：加速大规模无监督异构异常检测（加速），2021
神经网络
- AutoEncoder：全连接自编码器（使用重构误差作为异常分数）
- VAE：变分自编码器（使用重构误差作为异常分数），2013
- Beta-VAE：变分自编码器（通过改变gamma和容量自定义损失项），2018
- SO_GAAL：单目标生成对抗主动学习，2019
- MO_GAAL：多目标生成对抗主动学习，2019
- DeepSVDD：深度单类分类，2018
- AnoGAN：使用生成对抗网络的异常检测，2017
- ALAD：对抗性学习的异常检测，2018
- AE1SVM：基于自编码器的单类支持向量机，2019
- DevNet：使用偏差网络的深度异常检测，2019
基于图的
- R-Graph：通过R-图进行异常检测，2017
- LUNAR：通过图神经网络统一局部异常检测方法，2022

异常集成与异常检测器组合框架

异常集成
- FB：特征装袋，2005
- LSCP：局部选择并行异常集成的组合，2019
- XGBOD：基于极限提升的异常检测（有监督），2018
- LODA：轻量级在线异常检测器，2016
- SUOD：加速大规模无监督异构异常检测（加速），2021
- INNE：使用最近邻集成的孤立异常检测，2018
组合方法
- Average：通过平均分数进行简单组合，2015
- Weighted Average：通过加权平均分数进行简单组合，2015
- Maximization：通过取最大分数进行简单组合，2015
- AOM：最大值的平均，2015
- MOA：平均值的最大化，2015
- Median：通过取分数的中位数进行简单组合，2015
- Majority Vote：通过取标签的多数票进行简单组合（可以使用权重），2015

实用函数

数据
- generate_data：合成数据生成；正常数据由多元高斯分布生成，异常值由均匀分布生成，generate_data
- generate_data_clusters：集群中的合成数据生成；可以通过多个集群创建更复杂的数据模式，generate_data_clusters
统计
- wpearsonr：计算两个样本的加权皮尔逊相关系数，wpearsonr
实用工具
- get_label_n：通过将前n个异常分数分配为1将原始异常分数转换为二进制标签，get_label_n
- precision_n_scores：计算精度@排名n，precision_n_scores

PyOD的使用

API介绍

特别需要注意的是，异常检测算法基本都是无监督学习，所以只需要X（输入数据），而不需要y（标签）。PyOD的使用方法和Sklearn中聚类分析很像，它的检测器（detector）均有统一的API。所有的PyOD检测器clf均有统一的API以便使用。

fit(X): 用数据X来“训练/拟合”检测器clf。即在初始化检测器clf后，用X来“训练”它。
fit_predict_score(X, y): 用数据X来训练检测器clf，并预测X的预测值，并在真实标签y上进行评估。此处的y只是用于评估，而非训练
decision_function(X): 在检测器clf被fit后，可以通过该函数来预测未知数据的异常程度，返回值为原始分数，并非0和1。返回分数越高，则该数据点的异常程度越高
predict(X): 在检测器clf被fit后，可以通过该函数来预测未知数据的异常标签，返回值为二分类标签（0为正常点，1为异常点）
predict_proba(X): 在检测器clf被fit后，预测未知数据的异常概率，返回该点是异常点概率

当检测器clf被初始化且fit(X)函数被执行后，clf就会生成两个重要的属性：

decision_scores: 数据X上的异常打分，分数越高，则该数据点的异常程度越高
labels_: 数据X上的异常标签，返回值为二分类标签（0为正常点，1为异常点）

不难看出，当我们初始化一个检测器clf后，可以直接用数据X来“训练”clf，之后我们便可以得到X的异常分值（clf.decision_scores）以及异常标签（clf.labels_）。当clf被训练后（当fit函数被执行后），我们可以使用decision_function()和predict()函数来对未知数据进行训练。

示例代码：

from pyod.models.knn import KNN
from pyod.utils.data import generate_data

# Generate sample data
X_train, X_test, y_train, y_test = generate_data(n_train=200, n_test=100, n_features=2, contamination=0.1)

# Initialize the KNN detector
clf = KNN()

# Train the detector
clf.fit(X_train)

# Get the outlier scores
y_train_scores = clf.decision_scores_  # raw outlier scores on the training data
y_test_scores = clf.decision_function(X_test)  # predict raw anomaly scores on the test data

PyOD实战

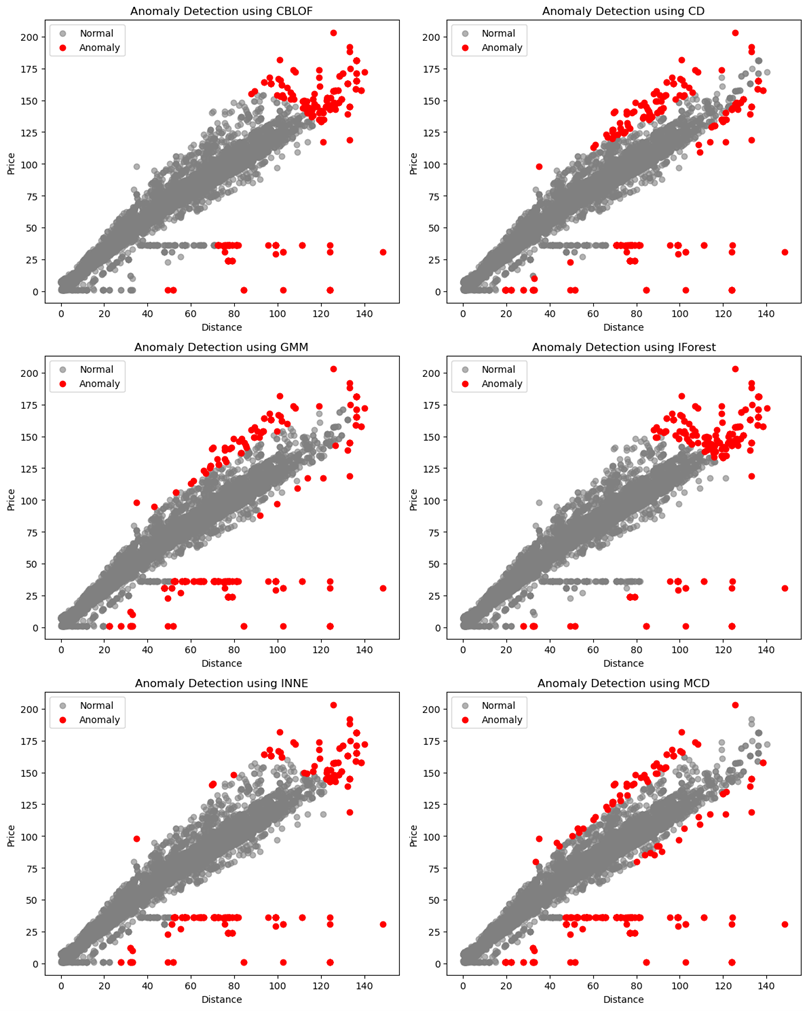
价格异常检测

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from pyod.models.auto_encoder import AutoEncoder
from pyod.models.cblof import CBLOF
from pyod.models.cd import CD
from pyod.models.gmm import GMM
from pyod.models.iforest import IForest
from pyod.models.inne import INNE
from pyod.models.mcd import MCD
from pyod.models.ocsvm import OCSVM
from pyod.models.xgbod import XGBOD

data = pd.read_csv("data.csv")

# 数据标准化
scaler = StandardScaler()
X_norm = scaler.fit_transform(X)

# 模型列表
models = [
    ("CBLOF", CBLOF(contamination=0.02)),
    ("CD", CD(contamination=0.02)),
    ("GMM", GMM(contamination=0.02)),
    ("IForest", IForest(contamination=0.02)),
    ("INNE", INNE(contamination=0.02)),
    ("MCD", MCD(contamination=0.02)),
]

# 设置图形布局
fig, axs = plt.subplots(3, 2, figsize=(12, 15))
axs = axs.flatten()

# 训练和绘制结果
for i, (name, model) in enumerate(models):
    model.fit(X_norm)
    y_pred = model.predict(X_norm)

    axs[i].scatter(X[y_pred == 0][:, 0], X[y_pred == 0][:, 1], color='grey', label='Normal', alpha=0.6)
    axs[i].scatter(X[y_pred == 1][:, 0], X[y_pred == 1][:, 1], color='red', label='Anomaly')

    # 设置标题和标签
    axs[i].set_title(f'Anomaly Detection using {name}')
    axs[i].set_xlabel('Distance')
    axs[i].set_ylabel('Price')
    axs[i].legend()

# 移除多余的子图
for j in range(len(models), len(axs)):
    fig.delaxes(axs[j])

# 显示图形
plt.tight_layout()
plt

参考链接：

Python异常检测包：PyOD

PyOD简介