在数据挖掘中,一个最基本的问题就是比较两个集合的相似度。通常通过遍历这两个集合中的所有元素,统计这两个集合中相同元素的个数,来表示集合的相似度;这一步也可以看成特征向量间相似度的计算(欧氏距离,余弦相似度)。当这两个集合里的元素数量异常大(特征空间维数很大),同时又有很多个集合需要判断两两间的相似度时,传统方法会变得十分耗时,最小哈希(minHash)可以用来解决该问题。
跟SimHash一样,MinHash也是LSH的一种,可以用来快速估算两个集合的相似度。MinHash由Andrei Broder提出,最初用于在搜索引擎中检测重复网页。它也可以应用于大规模聚类问题。
minHash最小哈希
假设现在有4个集合,分别为S1,S2,S3,S4;其中,S1={a,d}, S2={c}, S3={b,d,e}, S4={a,c,d},所以全集U={a,b,c,d,e}。我们可以构造如下0-1矩阵:
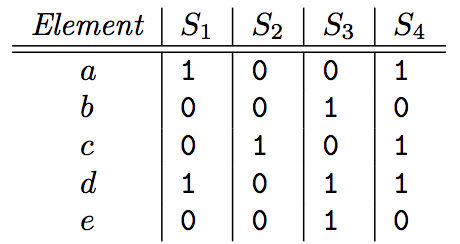
为了得到各集合的最小哈希值,首先对矩阵进行随机行打乱,则某集合(某一列)的最小哈希值就等于打乱后的这一列第一个值为1的行所在的行号。举一个例子:
定义一个最小哈希函数h,用于模拟对矩阵进行随机行打乱,打乱后的0-1矩阵为:
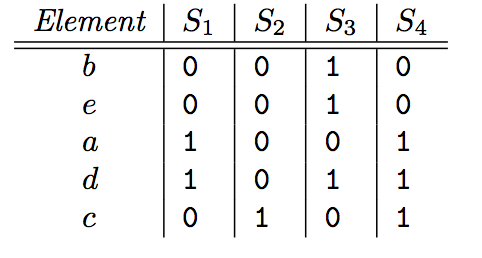
如图所示,h(S1)=2, h(S2)=4, h(S3)=0, h(S4)=2。
性质:对于一个随机的排列,两个集合的minHash相等的概率等于两个集合的Jaccard相似度
$$Pr[minHash(A)=minHash(B)]=J(A,B)$$
证明:假设{S1,…SM}{S1,…SM}M个集合共有N个元素,即那个矩阵有N行,minHash的思想是随机选取n个排列,n<<N,那么我们可以用minHash得到的n维度向量$[h1(S),…,hn(S)]^T$来代替集合S,可以看出原来N维度的向量被压缩为了n维度。在现实中排列一个很大的行索引也是很慢的,所以一般用随机的哈希函数来替代排列。
还是依据上面的矩阵表示,我们这里用两个哈希函数(x+1 mod5和3x+1 mod5)代表两个排列:
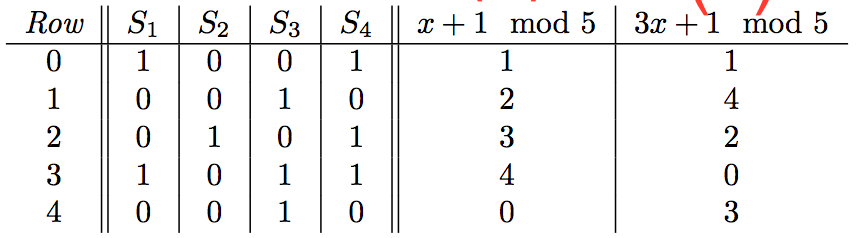
对于第一个排列(x+1 mod5)的含义,新第0行对应的第4行,新的第一行为原来的第0行,所以第一个排列的顺序为[4 0 1 2 3 4],第二个排列为[3 0 2 4 1].那么根据minHash的定义,我们可以得到:
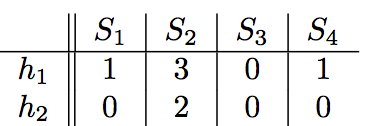
当然这是我们根据肉眼看的,那么如何通过一个算法得到呢?
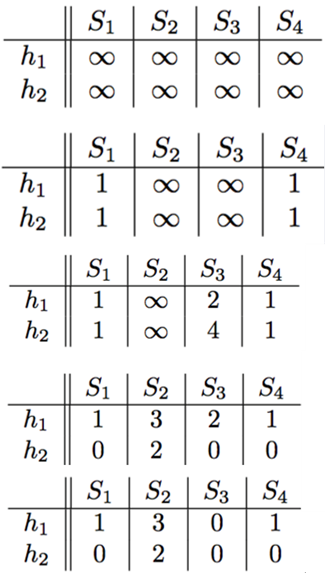
若S表示集合的矩阵表示。初始化新的minHash矩阵K,每列代表一个集合,每行代表一个排列,矩阵每个元素初始化为∞.下面N代表原来的feature个数,n代表新的排列个数,M代表集合个数。在实例中N=5, n=2, M=4
- 根据哈希算出每行的h1(i),…,hn(i).(i=1…N)
- For i=1:N
- For c=1:M
- 如果S[i,c]为0;跳过
- 否则;对于每个排列r=1…n, K(r,c)=min(K(r,c),h_r(i))
上述例子的更新过程如下:
通过上面的过程,每个集合就可以用一个n维向量来表示,已经大大压缩了数据,然而面对海量数据,若要找出任意两个点的相似度,依然是一个很大的计算量。然后在很多应用中,我们之需要找出与某点相似的点的集合即可,而不用算出每个pair对的相似度。
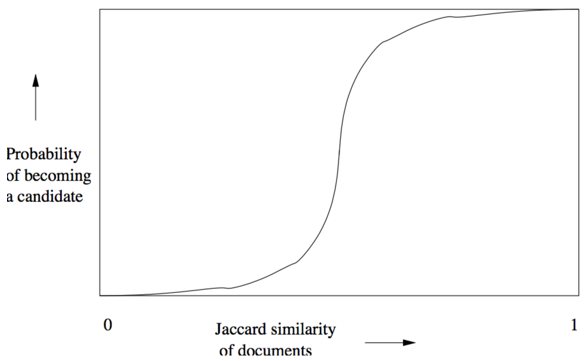
上面得到向量可以分为b段(桶),每个段有r个行,假设两个点的Jaccard相似度为s,根据”minHash的值相等的概率等于Jaccard相似度”这个定理,若两个点在某个段完全相同,则认为这两个点为相似对。分析如下:
- 两个点在一个段中,完全一样的概率为$s^r$
- 两个点在一个段中,不完全一样的概率为$1-s^r$
- 两个点在所有段中,不完全一样的概率为$(1-s^r)^b$
- 两个点至少有一个段相同的概率为$1-(1-s^r)^b$
最后一行的这个函数可以画成一个S曲线,横轴为Jaccard相似度,纵轴为被选择为相似对的概率 :
根据上述技术(Banding Technique),就可以高效率的找出任意点的相似点有哪些。
MinHash的应用
MinHash可以应用在推荐系统中,将上述0-1矩阵的横轴看成商品,竖轴看成用户,有成千上万的用户对有限的商品作出购买记录,具体可以参考基于协同过滤,NMF和Baseline的推荐算法一文。MinHash也可以应用在自然语言处理的文本聚类中,将上述0-1矩阵的横轴看成文档,竖轴看成词汇或n-gram。
Minhash与simhash的比较
谷歌新闻推荐论文中使用到了Minhash。这里涉及推荐,使用用户看过的所有的新闻集合表示用户。这里每个用户可以用一个取值0/1的向量表示(每个维度代表新闻,取值代表是否看过该新闻)。这里选用的方法是MinHash。文章将MinHash看作是聚类算法,因为哈希后的不同桶可以看作不同的簇。具体算法是对用户看过的新闻集合进行随机排列,第一个新闻的序号就是最小哈希的结果。但是由于新闻集合太大,显示的随机排列是不可取的。文章里面用哈希的方法模拟随机排列的过程,将每个新闻哈希到0到N,取哈希结果最小的那篇新闻的序号即可。
谷歌网页去重论文中使用到了Simhash。这里用一个高维向量表示表示一个网页。这里每维度的值是一个实数(不是binary)故选用SimHash。使用SimHash将高维向量降维成64位0/1的指纹。之后文章提出了如何找出指纹库中与给定指纹相差最多3位的所有指纹,查询效率关于时间和空间的权衡
参考链接:



