指标波动归因贡献率计算

指标波动贡献率

指标波动贡献率是一种用于分析和衡量不同因素对某一指标变动影响的统计方法。它在经济学、金融学、市场分析以及其他领域中被广泛应用。通过分析指标波动贡献率，可以更好地理解各个因素在指标变动中所起的作用，从而帮助决策者做出更明智的决策。

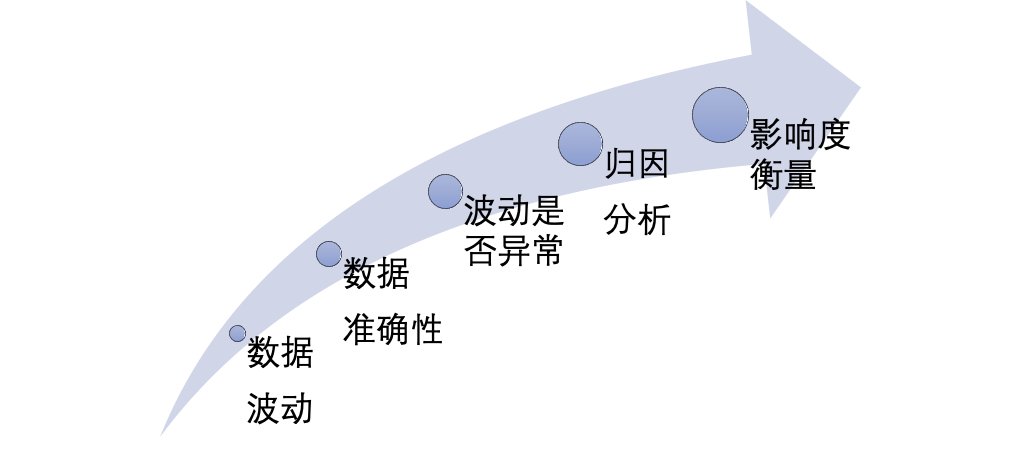
基本概念：

• 指标：这是指你感兴趣的主要变量或度量，例如股票价格、GDP增长率、销售额等。
• 波动：这是指指标在特定时间段内的变化幅度或变动性。
• 贡献率：这是指各个因素对指标波动的贡献程度，通常以百分比表示。

贡献率

贡献率是一个用来衡量某个特定因素或部分对整体产生影响程度的指标。通常用百分比表示，贡献率帮助分析和理解各个组成部分对整体结果的影响或贡献。

贡献率的基本概念

• 定义：贡献率指的是一个部分对整体的贡献程度，通常用来表示某一因素在总体中的相对重要性或影响力。
• 计算方法：贡献率通常是通过将某一部分的值除以整体的总值，然后乘以100%来计算的。公式如下：

$$ \text{贡献率} = ( \frac{\text{某部分的值}}{\text{整体的总值}}) \times 100% $$

应用实例

• 财务分析：在企业财务中，贡献率可以用于分析某一产品线或部门对公司总收入或利润的贡献。
• 市场营销：在市场营销中，贡献率可以用于评估某一广告活动对总销售额增长的贡献。
• 经济分析：在宏观经济学中，可以分析不同产业对GDP增长的贡献率。

优势

• 识别关键因素：通过贡献率，能够识别出对整体影响最大的因素或部分。
• 资源分配优化：帮助决策者更好地进行资源分配，集中力量在贡献率高的领域。
• 绩效评估：用于评估和比较不同部门、产品线或策略的相对表现。

局限性

• 数据依赖性：贡献率的计算高度依赖于数据的准确性和完整性。
• 动态变化：贡献率是一个动态指标，可能会随着时间或条件的变化而变化。
• 忽略交互效应：贡献率通常不考虑不同因素之间的交互效应，可能导致对复杂系统的简化理解。

计算步骤

• 识别相关因素：确定可能影响指标变化的所有相关因素。这可能包括宏观经济因素、市场动态、政策变化等。
• 数据收集：收集关于指标和相关因素的数据。
• 模型建立：建立一个统计模型（如回归分析、方差分析等），以量化各个因素对指标波动的影响。
• 计算贡献率：通过模型分析计算出每个因素对指标总波动的贡献率。
• 结果解释：分析和解释各个因素的贡献率，了解哪些因素是主要驱动因素。

总之，贡献率是一个重要的分析工具，能够提供对整体系统中各个部分影响的洞察，帮助在决策和战略规划中做出更为明智的选择。

可加型指标波动贡献率的计算

可加型指标波动贡献率是用于分析和量化各个组成部分对整体指标变化贡献的工具。这种方法特别适用于可加型指标，即总值是各个部分之和的指标，如总销售额、总收入、总成本等。

计算步骤

• 识别总指标和组成部分：
  • 确定你要分析的总指标（例如，总销售额）。
  • 确定该指标的各个组成部分（例如，不同产品线的销售额）。
• 数据收集：
  • 收集不同时期的总指标和各组成部分的数据。
• 计算变化量：
  • 计算每个组成部分在不同时间段的变化量。
  • 计算总指标在同一时间段的变化量。
• 计算贡献率：
  • 对于每个组成部分，计算其对总指标变化的贡献率。公式如下：$$\text{贡献率} = \left( \frac{\text{组成部分的变化量}}{\text{总指标的变化量}} \right) \times 100% $$
  • 需要注意的是，总指标的变化量不能为零，否则无法计算贡献率。
• 结果分析：
  • 分析各个组成部分的贡献率，确定哪些部分对总指标的变化贡献最大。

示例场景

假设某公司有三个产品线A、B、C，其销售额分别为：

• 期初总销售额 = 1000万元（A: 300万元, B: 400万元, C: 300万元）
• 期末总销售额 = 1200万元（A: 350万元, B: 450万元, C: 400万元）

变化量计算：

• 产品线A变化量 = 350 – 300 = 50万元
• 产品线B变化量 = 450 – 400 = 50万元
• 产品线C变化量 = 400 – 300 = 100万元
• 总销售额变化量 = 1200 – 1000 = 200万元

贡献率计算：

• 产品线A贡献率 = (50 / 200) × 100% = 25%
• 产品线B贡献率 = (50 / 200) × 100% = 25%
• 产品线C贡献率 = (100 / 200) × 100% = 50%

Python实现

使用Python和Pandas库可以更加高效地处理数据，特别是当涉及到多个维度的组合时。下面是一个示例，展示如何使用Pandas来计算可加型指标波动贡献率，并考虑维度组合（例如，不同产品线和地区的组合）。

假设我们有一个包含产品线、地区、期初销售额和期末销售额的数据集。我们希望计算每个维度组合对总销售额变化的贡献率。

import pandas as pd

# 创建示例数据集
data = {
    '产品线': ['A', 'A', 'B', 'B', 'C', 'C'],
    '地区': ['North', 'South', 'North', 'South', 'North', 'South'],
    '期初销售额': [300, 200, 400, 300, 300, 200],
    '期末销售额': [350, 250, 450, 350, 400, 300]
}

# 将数据转换为DataFrame
df = pd.DataFrame(data)

# 计算每个组合的变化量
df['变化量'] = df['期末销售额'] - df['期初销售额']

# 计算总变化量
total_change = df['变化量'].sum()

# 确保总变化量不为零
if total_change == 0:
    raise ValueError("Total change is zero, cannot calculate contribution rate.")

# 计算每个组合的贡献率
df['贡献率'] = (df['变化量'] / total_change) * 100

# 输出结果
print(df[['产品线', '地区', '期初销售额', '期末销售额', '变化量', '贡献率']])

# 如果需要按照某个维度进行汇总，例如产品线或地区，可以使用groupby
grouped = df.groupby('产品线').agg({
    '期初销售额': 'sum',
    '期末销售额': 'sum',
    '变化量': 'sum'
})

# 计算汇总后的贡献率
grouped['贡献率'] = (grouped['变化量'] / total_change) * 100

# 输出汇总结果
print("\n按产品线汇总的贡献率:")
print(grouped)

乘法型指标波动贡献率的计算

乘法型指标波动贡献率涉及到的指标不是简单的加法关系，而是乘法关系。例如，销售额可以表示为“价格*数量”，这种情况下，我们需要分析价格和数量各自对销售额变化的贡献。

在分析乘法型指标波动贡献率时，通常有两种方法可以使用：直接的线性近似法和对数方法。每种方法都有其独特的优点和适用场景。

线性近似法

使用微分的思想，通过计算每个因素的偏差以及它们对结果指标的直接影响来分析贡献。

计算步骤

要计算每个因素对$Z$波动的贡献率，可以使用以下步骤：

• 基准值计算：首先确定各因素的基准值，通常是某一时期的实际值或平均值。
• 偏差计算：计算每个因素相对于基准值的偏差。例如，若A的基准值为$A_0$，实际值为$A_1$，则偏差为$A_1 – A_0$。
• 影响量计算：对于每个因素，计算其对Z的影响量。可以使用全微分近似的方法来估算：$\Delta Z \approx \frac{\partial Z}{\partial A} \Delta A + \frac{\partial Z}{\partial B} \Delta B + \cdots$。其中，(\frac{\partial Z}{\partial A} = \frac{Z}{A}) 是关于A的偏导数，表示A的微小变化对Z的影响。
• 贡献率计算：计算每个因素的贡献率，定义为其影响量在总波动中的占比：$\text{贡献率}_A = \frac{\frac{\partial Z}{\partial A} \Delta A}{\Delta Z}$。依此类推，计算其他因素的贡献率。
• 结果分析：根据计算的贡献率，可以分析各因素对指标波动的相对重要性。

优点：

• 计算简单，直观地反映了每个因素的绝对变化对结果的影响。
• 适用于因素变化较小的情况，因为在这种情况下线性近似能较好地描述实际变化。

缺点：

• 当因素变化较大时，线性近似可能不够准确，因为忽略了高阶变化。
• 不能很好地处理比例变化（相对变化）的影响，尤其是在因素变化显著的情况下。

Python实现

import pandas as pd

# 示例数据
data = {
    'A': [10, 12, 15],  # 因素A在不同时期的值
    'B': [5, 6, 8],     # 因素B在不同时期的值
    'C': [2, 2, 3]      # 因素C在不同时期的值
}

# 创建DataFrame
df = pd.DataFrame(data)

# 计算指标Z = A * B * C
df['Z'] = df['A'] * df['B'] * df['C']

# 计算基准值，通常是第一个时间点的值
base_values = df.iloc[0]

# 计算每个因素的偏差
df['Delta_A'] = df['A'] - base_values['A']
df['Delta_B'] = df['B'] - base_values['B']
df['Delta_C'] = df['C'] - base_values['C']

# 计算每个因素对Z的影响量
df['Impact_A'] = (base_values['B'] * base_values['C']) * df['Delta_A']
df['Impact_B'] = (base_values['A'] * base_values['C']) * df['Delta_B']
df['Impact_C'] = (base_values['A'] * base_values['B']) * df['Delta_C']

# 计算总波动
df['Delta_Z'] = df['Z'] - base_values['Z']

# 计算贡献率
df['Contribution_A'] = df['Impact_A'] / df['Delta_Z']
df['Contribution_B'] = df['Impact_B'] / df['Delta_Z']
df['Contribution_C'] = df['Impact_C'] / df['Delta_Z']

# 输出结果
print(df[['A', 'B', 'C', 'Z', 'Contribution_A', 'Contribution_B', 'Contribution_C']])

对数方法

通过对数变换，将乘法关系转换为加法关系，以捕捉比例变化。公式：$\ln(Z) = \ln(A) + \ln(B) + \ln(C)$

计算步骤

• 识别指标关系：确定指标的乘法关系。例如，某指标$Z = X \times Y$。
• 数据收集：收集指标在不同时期的数据。例如，期初和期末的X和Y值。
• 计算变化量：计算每个因子的变化率。
• 计算贡献率：
  • 使用对数方法来分解贡献。假设期初指标$Z_0 = X_0 \times Y_0$，期末指标$ Z_1 = X_1 \times Y_1$。
  • 计算$\Delta \ln X = \ln(X_1) – \ln(X_0)$和$\Delta \ln Y = \ln(Y_1) – \ln(Y_0)$。
  • 近似地，指标的变化可以表示为：$\Delta \ln Z \approx \Delta \ln X + \Delta \ln Y$。
  • 因此，X对 Z的贡献率为 $\frac{\Delta \ln X}{\Delta \ln Z}$， Y 对Z的贡献率为 $\frac{\Delta \ln Y}{\Delta \ln Z}$。

优点：

• 能够更好地捕捉到因素的相对变化，适合处理变化幅度较大的情况。
• 转换后的加法关系使得各因素的相对贡献更加直观。
• 对于多个因素的组合变化，对数方法能更准确地反映其对结果的影响。

缺点：

• 对数变换可能在某些情况下不直观，特别是对不熟悉对数性质的用户。
• 不能处理因素值为零或负值的情况，因为对数函数在这些点上未定义。

Python实现

import pandas as pd
import numpy as np

# 示例数据
data = {
    'A': [10, 12, 15],  # 因素A在不同时期的值
    'B': [5, 6, 8],     # 因素B在不同时期的值
    'C': [2, 2, 3]      # 因素C在不同时期的值
}

# 创建DataFrame
df = pd.DataFrame(data)

# 计算指标Z = A * B * C
df['Z'] = df['A'] * df['B'] * df['C']

# 计算对数值
df['ln_A'] = np.log(df['A'])
df['ln_B'] = np.log(df['B'])
df['ln_C'] = np.log(df['C'])
df['ln_Z'] = np.log(df['Z'])

# 计算基准值，通常是第一个时间点的对数值
base_values = df.iloc[0]

# 计算对数变化
df['Delta_ln_A'] = df['ln_A'] - base_values['ln_A']
df['Delta_ln_B'] = df['ln_B'] - base_values['ln_B']
df['Delta_ln_C'] = df['ln_C'] - base_values['ln_C']

# 计算总对数变化
df['Delta_ln_Z'] = df['ln_Z'] - base_values['ln_Z']

# 计算贡献率
df['Contribution_ln_A'] = df['Delta_ln_A'] / df['Delta_ln_Z']
df['Contribution_ln_B'] = df['Delta_ln_B'] / df['Delta_ln_Z']
df['Contribution_ln_C'] = df['Delta_ln_C'] / df['Delta_ln_Z']

# 输出结果
print(df[['A', 'B', 'C', 'Z', 'Contribution_ln_A', 'Contribution_ln_B', 'Contribution_ln_C']])

选择方法的考虑因素

• 变化幅度：如果各因素的变化较小，线性近似法可能足够。如果变化较大，对数方法更合适。
• 分析目标：如果更关注绝对变化，线性近似法可能更直观。如果关注相对变化和比例影响，对数方法更合适。
• 数据特性：对数方法要求所有数据为正且非零，而线性近似法对数据没有这样的限制。

两种方法各有优缺点，选择哪种方法取决于具体的分析需求和数据特性。在实际应用中，可能需要结合使用两种方法，以获得更全面的分析视角。例如，可以先用线性近似法进行初步分析，然后用对数方法来深入探讨相对变化的贡献。这样可以提供对指标波动的更全面理解。

除法型指标波动贡献率的计算

除法型指标波动贡献率的计算涉及到的指标是通过除法关系定义的，例如“利润率=利润/收入”。在这种情况下，我们需要分析分子和分母的变化对指标变化的贡献。

除法型指标波动贡献率和乘法型指标波动贡献率类似，通常有两种方法可以使用：

线性近似法

计算步骤

对于小的变化，使用线性近似法可以有效地分析贡献：

• 偏导数计算：
  • 对 A 的偏导数：$\frac{\partial Z}{\partial A} = \frac{1}{B}$
  • 对 B 的偏导数：$\frac{\partial Z}{\partial B} = -\frac{A}{B^2}$
• 影响量计算：
  • A 的影响量：$\Delta Z_A \approx \frac{1}{B_0} \Delta A$
  • B 的影响量：$\Delta Z_B \approx -\frac{A_0}{B_0^2} \Delta B$
• 贡献率计算：
  • 总变化：$\Delta Z = Z_1 – Z_0 = \frac{A_1}{B_1} – \frac{A_0}{B_0}$
  • 贡献率：$\text{贡献率}_A = \frac{\Delta Z_A}{\Delta Z}$,$\text{贡献率}_B = \frac{\Delta Z_B}{\Delta Z}$

Python实现

import pandas as pd

# 示例数据
data = {
    'A': [100, 120, 150],  # 因素A在不同时期的值
    'B': [20, 25, 30]      # 因素B在不同时期的值
}

# 创建DataFrame
df = pd.DataFrame(data)

# 计算指标Z = A / B
df['Z'] = df['A'] / df['B']

# 基准值（通常为第一个时间点的值）
base_values = df.iloc[0]

# 线性近似法计算贡献
df['Delta_A'] = df['A'] - base_values['A']
df['Delta_B'] = df['B'] - base_values['B']
df['Impact_A'] = (1 / base_values['B']) * df['Delta_A']
df['Impact_B'] = -(base_values['A'] / base_values['B']**2) * df['Delta_B']
df['Delta_Z'] = df['Z'] - base_values['Z']
df['Contribution_A'] = df['Impact_A'] / df['Delta_Z']
df['Contribution_B'] = df['Impact_B'] / df['Delta_Z']

# 输出结果
print("线性近似法结果：")
print(df[['A', 'B', 'Z', 'Contribution_A', 'Contribution_B']])

对数方法

计算方法

对数方法可以用于分析相对变化：

• 对数变换：$ln(Z) = \ln(A) – \ln(B)$
• 对数变化：$\Delta \ln(Z) = \Delta \ln(A) – \Delta \ln(B)$
• 贡献率计算：
  • $\text{贡献率}{\ln A} = \frac{\Delta \ln(A)}{\Delta \ln(Z)}$
  • $\text{贡献率}{\ln B} = -\frac{\Delta \ln(B)}{\Delta \ln(Z)}$

Python实现

import numpy as np

# 计算对数值
df['ln_A'] = np.log(df['A'])
df['ln_B'] = np.log(df['B'])
df['ln_Z'] = np.log(df['Z'])

# 基准值（通常为第一个时间点的对数值）
base_ln_values = df.iloc[0]

# 对数方法计算贡献
df['Delta_ln_A'] = df['ln_A'] - base_ln_values['ln_A']
df['Delta_ln_B'] = df['ln_B'] - base_ln_values['ln_B']
df['Delta_ln_Z'] = df['ln_Z'] - base_ln_values['ln_Z']
df['Contribution_ln_A'] = df['Delta_ln_A'] / df['Delta_ln_Z']
df['Contribution_ln_B'] = -df['Delta_ln_B'] / df['Delta_ln_Z']

# 输出结果
print("\n对数方法结果：")
print(df[['A', 'B', 'Z', 'Contribution_ln_A', 'Contribution_ln_B']])

参考链接：

• 转化指标波动分析之维度拆解 – 标点符 (biaodianfu.com)