直方图简介
在统计学中,直方图(英语:Histogram)是一种对数据分布情况的图形表示,是一种二维统计图表,它的两个坐标分别是统计样本和该样本对应的某个属性的度量,以长条图(bar)的形式具体表现。因为直方图的长度及宽度很适合用来表现数量上的变化,所以较容易解读差异小的数值。
直方图(Histogram)是一种可视化在连续间隔,或者是特定时间段内数据分布情况的图表,经常被用在统计学领域。简单来说,直方图描述的是一组数据的频次分布。直方图有助于我们知道数据的分布情况,诸如众数、中位数的大致位置、数据是否存在缺口或者异常值。
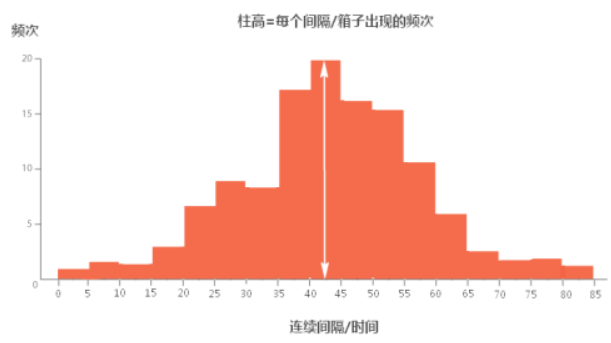
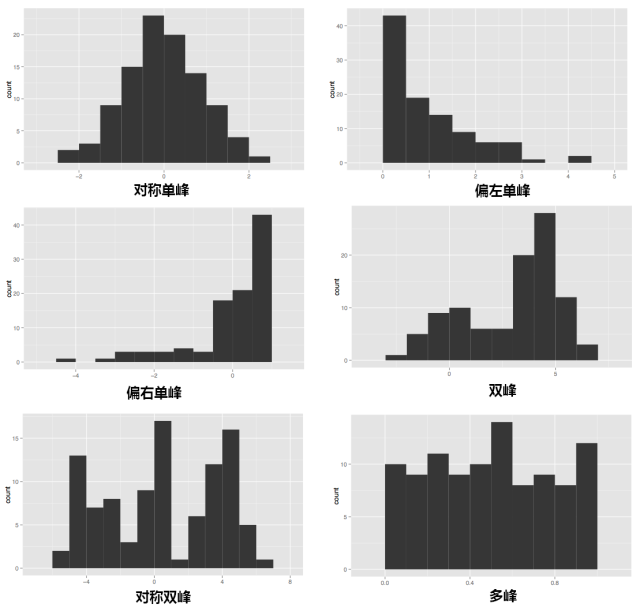
根据数据分布状况不同,直方图展示的数据有不同的模式,包括对称单峰、偏左单峰、偏右单峰、双峰、多峰以及对称多峰。
直方图与柱状图的差别
直方图和柱状图最让人迷惑的地方,就是它们长得非常相似。实际上,直方图和柱状图无论是在图表意义、适用数据上,还是图表绘制上,都有很大的不同。
1.直方图展示数据的分布,柱状图比较数据的大小。
这是直方图与柱状图最根本的区别。举个例子,有10个苹果,每个苹果重量不同。如果使用直方图,就展示了重量在0-10g的苹果有多少个,10-20g的苹果有多少个;如果使用柱状图,则展示每个苹果的具体重量。
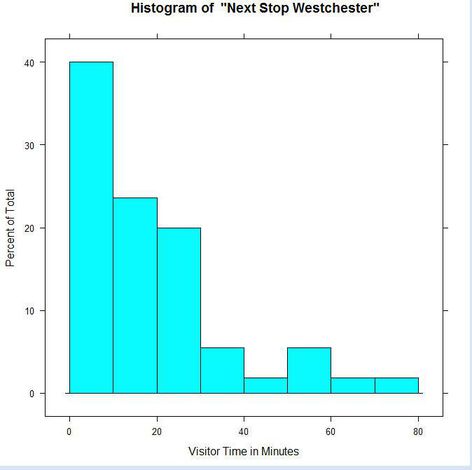
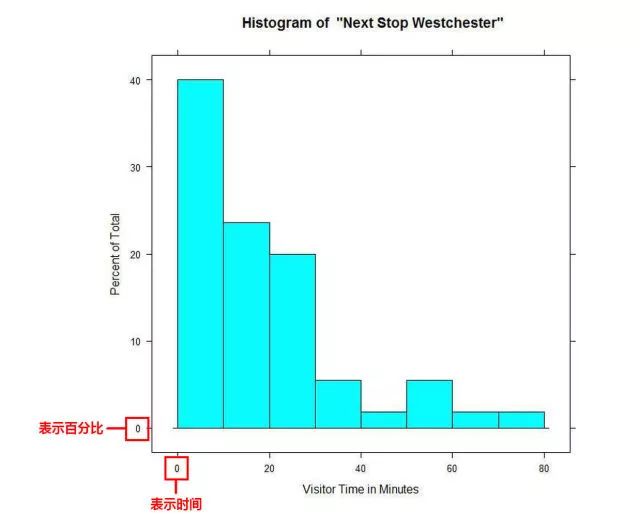
所以直方图展示的是一组数据中,在你划分的区间里,这些数据的分布情况,但是我们不知道在一个区间里,单个数据的具体大小。下图展现了游客在博物馆的游览时间,其中,将近40%的游客仅逗留了0-10分钟。但是我们无法知道这些游客中,每个人具体的游览时间是多少。
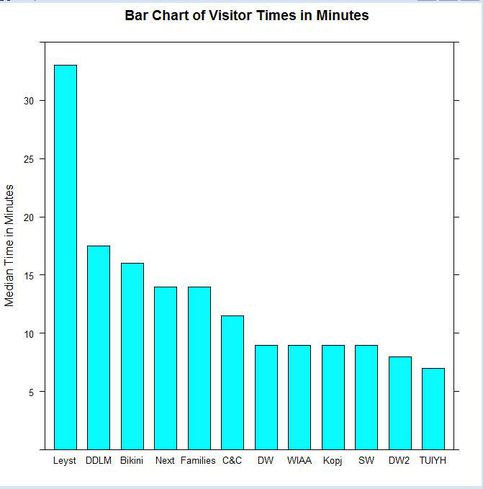
而在柱状图里,我们能看到的是每个数据的大小,并且进行比较。下图就比较了在12次展览中,参观者参观时间的中位数,我们能够知道参观的具体用时。
2.直方图X轴为定量数据,柱状图X轴为分类数据。
由图表的原理就决定了,X轴在直方图与柱状图中的用法是不一样的。在直方图中,X轴上的变量是一个个连续的区间,这些区间通常表现为数字,例如代表苹果重量的“0-10g,10-20g……”,代表时间长度的“0-10min,10-20min……”。而在柱状图中,X轴上的变量是一个个分类数据,例如不同的国家名称、不同的游戏类型。
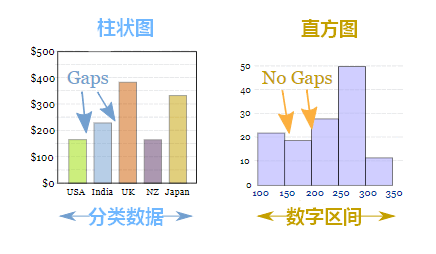
因此,直方图上的每根柱子都是不可移动的,X轴上的区间是连续的、固定的。而柱状图上的每根柱子是可以随意排序的,有的情况下需要按照分类数据的名称排列,有的则需要按照数值的大小排列。
3.直方图柱子无间隔,柱状图柱子有间隔
因为直方图中的区间是连续的,因此柱子之间不存在间隙。而柱状图的柱子之间是存在间隔。还有一个值得注意的地方,在直方图中,第一根柱子应该和Y轴有一定的间隔,即使都是从“0”这个值开始的。因为X轴与Y轴上“0”的意义不同,而且很多直方图上的区间并不是从0开始的。
4.直方图柱子宽度可不一,柱状图柱子宽度须一致
柱状图柱子的宽度因为没有数值含义,所以宽度必须一致。但是在直方图中,柱子的宽度代表了区间的长度,根据区间的不同,柱子的宽度可以不同,但理论上应为单位长度的倍数。
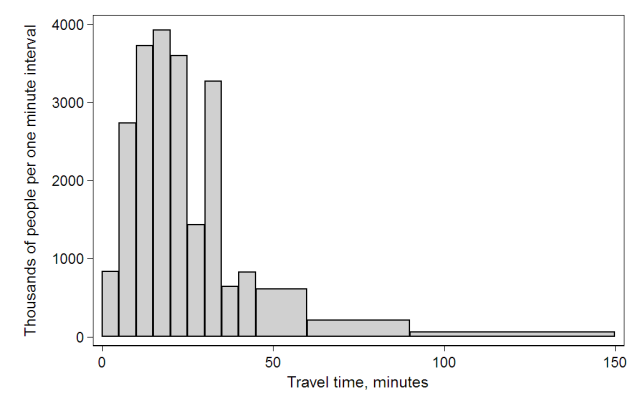
例如,美国人口普查局(The U.S. Census Bureau)调查了12.4亿人的上班通勤时间,由于通勤时间在45-150分钟的人数太少,因此区间改为45-60分钟、60-90分钟、90-150分钟,其他组距则均为5。
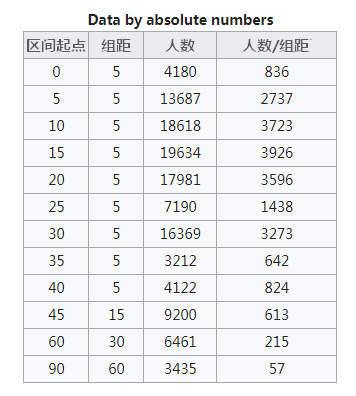
可以看到,Y轴的数据为“人数/组距”,在这种情况下,每个柱子的面积相加就等于调查的总人数,柱子的面积就有了意义。
直方图绘制
在绘制直方图时,最困难的是设置合适的直方图中的bins值。
不管使用matplotlib.pyplot.hist或是pandas.DataFrame.hist最终调用的是numpy.histogram。我们先来看下numpy.histogram方法:
numpy.histogram(a, bins=10, range=None, normed=None, weights=None, density=None)
参数
- a:array_like,需要处理的数据
- bins:int或序列或str
- 如果是int,则数据会进行按给定的值平均划分
- 如果给定的序列,则按序列的给定的数值进行边界划分(包括右边值)
- 如果传入的是字符串,则使用histogram_bin_edges定义的字符串类型
- range(float, float):可选,设定需要划分的数据的范围,默认为(a.min(), a.max())
- weights:array_like,可选,给字符串的权重
- density:布尔类型,如果为False,则显示具体的数量,如果为True则显示占比
numpy.histogram_bin_edges定义的字符串类型
- auto:sturges或fd估算器中较大的那个值。提供良好的全方位性能。
- sqrt:使用的平方根(数据大小)估计量,以求其速度和简便性。公式:$n_h=\sqrt{n}$
- rice:估计器不考虑可变性,仅考虑数据大小。通常会高估所需的箱数量。公式:$n_h=2\sqrt[3]{n}$
- sturges:R的默认方法,仅考虑数据大小。仅对高斯数据最佳,而对于大型非高斯数据集则低估了bin的数量。公式:$n_h=\log_{2}{n}+1$
- fd:Freedman Diaconis Estimator,考虑到数据可变性和数据大小的稳健(对异常值具有弹性)的估计器。公式: $h=2\frac{IQR}{n^{1/3}}$,其中 IQR 为四分位距,详细介绍见箱形图简介
- scott:考虑数据变异性和数据大小的鲁棒估计器。公式:$h=\sigma\sqrt[3]{\frac{24\ast\sqrt{\pi}}{n}}$,与标准差成正比,与数据量立方根成反比,对于小数据集来说可能过于保守,但对于大数据集来说非常好。标准差对异常值不是很稳健,在没有异常值的情况下,值与 Freedman-Diaconis 估计非常相似。
- stone:基于平方根误差的 leave-one-out cross-validation(留一交叉验证)估计器。可以看作是 Scott 规则的概括。
doane:Sturges 估算器的改进版,可以更好地与非正常数据集配合使用。$n_h=1+\log_{2}{n}+\log_{2}{1+\frac{\left|g_1\right|}{\sigma_{g_1}}}, g_1=mean[(\frac{x-u}{\sigma})^3], \sigma_{g_1}=\sqrt{\frac{6(n-2)}{(n+1)(n+3)}}$
留一交叉验证
正常训练都会划分训练集和验证集,训练集用来训练模型,而验证集用来评估模型的泛化能力。留一交叉验证是一个极端的例子,如果数据集 D 的大小为 N,那么用 N-1 条数据进行训练,用剩下的一条数据作为验证,用一条数据作为验证的坏处就是可能 $E_{val}$ 和 $E_{out}$ 相差很大,所以在留一交叉验证里,每次从 D 中取一组作为验证集,直到所有样本都作过验证集,共计算 N 次,最后对验证误差求平均,得到 $Eloocv(H,A)$,这种方法称之为留一法交叉验证。
$$\frac{1}{N}\sum_{n=1}^{N}e_n=\frac{1}{N}\sum_{n=1}^{N}err(g_n^-(x_n),y_n)$$
至于为什么,其原因和为什么使用交叉验证是一样的,主要是为了防止过拟合,评估模型的泛化能力。
当数据集 D 的数量较少时使用留一交叉验证,其原因主要如下:
- 数据集少,如果像正常一样划分训练集和验证集进行训练,那么可以用于训练的数据本来就少,还被划分出去一部分,这样可以用来训练的数据就更少了。loocv 可以充分的利用数据。
- 因为 loocv 需要划分 N 次,产生 N 批数据,所以在一轮训练中,要训练出 N 个模型,这样训练时间就大大增加。所以 loocv 比较适合训练集较少的场景
为什么可以使用 LOOCV 来近似估计泛化误差,即 $E_{loocv}\approx E_{out}$,证明如下:
$$\begin{aligned}\mathcal{E}E_{\mathrm{loocv}}(\mathcal{H},\mathcal{A})=\sum_{\mathcal{D}}\frac{1}{N}\sum_{n=1}^{N}e_{n}&=\frac{1}{N}\sum_{n=1}^{N}\mathcal{E}_{\mathcal{D}}e_{n}\\&=\frac{1}{N}\sum_{n=1}^{N}\sum_{\mathcal{D}_{n}\left(\mathbf{x}_{n},y_{n}\right)}\sum_{\mathrm{Prr}}\left(g_{n}^{-}\left(\mathbf{x}_{n}\right),y_{n}\right)\\&=\frac{1}{N}\sum_{n=1}^{N}\sum_{\mathcal{D}_{n}}E_{\mathrm{out}}\left(g_{n}^{-}\right)\\&=\frac{1}{N}\sum_{n=1}^{N}\bar{E}_{\mathrm{out}}(N-1)=\overline{E_{\mathrm{out}}}(N-1)\end{aligned}$$
解释如下:
- $\varepsilon_{D}$ 表示在不同数据集上的期望,$\varepsilon$ 是表示期望的符号,这里不同的数据 D, 我的理解是对原始数据的 N 次划分得到的不同数据集
- $\varepsilon_{D}e_{n}=>\varepsilon_{D_{n}}\varepsilon_{{(x_{n},y_{n})}}e_{n}$ 是因为 $D_{n}$ 和 $(x_{n},y_{n})$ 服从 iid 分布
- $\varepsilon_{{(x_{n},y_{n})}}err(g_{n}^{-}(x_{n}),y_{n})$ 转化为 $E_{out}(g_{n}^{-})$ 是期望的定义和 $E_{out}$ 的定义,虽然是对剩下的一个求误差,但是求的是对剩下单个数据的期望,单个数据的的期望相当于对所有未知数据上求概率平均(因为训练数据和位置数据是 iid, 所以对训练数据求期望相当终于对未知数据求期望),也就是 $g_{n}^{-}$ 在未知数据上的 E 即 $E_{out}$
LOOCV 的优点:
- 充分利用数据
- 因为采样是确定的,所以最终误差也是确定的,不需要重复 LOOCV
LOOCV 的缺点:
- 训练起来耗时
- 由于每次只采一个样本作为验证,导致无法分层抽样,影响验证集上的误差。举个例子,数据集中有数量相等的两个类,对于一条随机数据,他的预测结果是被预测为多数的结果,如果每次划出一条数据作为验证,则其对应的训练集中则会少一条,导致训练集中该条数据占少数从而被预测为相反的类,这样原来的误差率为 50%,在 LOOCV 中为 100%
LOOCV 模型选择问题:
之前有个疑问就是,在留一交叉验证过后,到底选择哪一个模型作为最终的模型呢?比如一百条数据在 LOOCV 中训练了一百个模型,选择其中最好的一个吗,其实不是这样的。考虑一般的划分训练,train_data 七三划分为训练集和验证集,然后每一轮训练都会得到一个 $E_{val}$,训练到 $E_{val}$ 最低为止,此时的模型就是最终的模型。LOOCV 也是这样的,只不过原来每一轮的训练对应于 LOOCV 中划分 N 次训练 N 个模型,原来的 $E_{val}$ 对应于 LOOCV 每一轮 N 个误差的平均,这样一轮轮下来直到验证集上的误差最小,此时的模型就是最终需要的模型(这个模型内部有 N 个小模型)
参考链接: