什么是贝塞尔曲线
贝塞尔曲线的数学基础是早在1912年就广为人知的伯恩斯坦多项式。但直到1959年，当时就职于雪铁龙的法国数学家Paul de Casteljau才开始对它进行图形化应用的尝试，并提出了一种数值稳定的de Casteljau算法。然而贝塞尔曲线的得名，却是由于1962年另一位就职于雷诺的法国工程师Pierre Bézier的广泛宣传。他使用这种只需要很少的控制点就能够生成复杂平滑曲线的方法，来辅助汽车车体的工业设计。
贝塞尔曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。因为控制简便却具有极强的描述能力，贝塞尔曲线在工业设计领域迅速得到了广泛的应用。不仅如此，在计算机图形学领域，尤其是矢量图形学，贝塞尔曲线也占有重要的地位。今天我们最常见的一些矢量绘图软件，如Flash、Illustrator、CorelDraw等，无一例外都提供了绘制贝塞尔曲线的功能。甚至像Photoshop这样的位图编辑软件，也把贝塞尔曲线作为仅有的矢量绘制工具（钢笔工具）包含其中。
贝塞尔曲线在web开发领域同样占有一席之地。CSS3新增了transition-timing-function属性，它的取值就可以设置为一个三次贝塞尔曲线方程。在此之前，也有不少JavaScript动画库使用贝塞尔曲线来实现美观逼真的缓动效果。
贝塞尔曲线分类
贝塞尔曲线根据控制点的数量分为：
- 一阶贝塞尔曲线（2个控制点）
- 二阶贝塞尔曲线（3个控制点）
- 三阶贝塞尔曲线（4个控制点）
- n阶贝塞尔曲线（n+1个控制点）
如何绘制贝塞尔曲线
一阶贝塞尔曲线
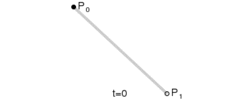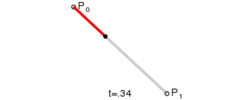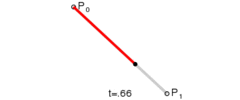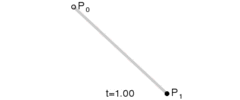
对于一阶贝塞尔曲线为我们可以看到是一条直线，通过几何知识，很容易根据t的值得出线段上那个点的坐标：
$$B_1(t)=P_0+(P_1-P_0)t$$
然后可以得出：
$$B_1(t)=(1-t)P_0+tP_1,t\in[0,1]$$
二阶贝塞尔曲线
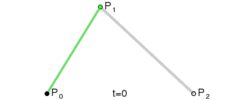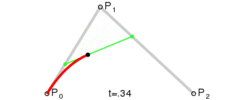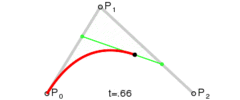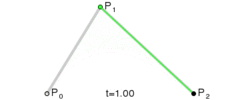
对于二阶贝塞尔曲线，其实你可以理解为：在$P_0P_1$上利用一阶公式求出点$P_0^{‘}$，然后在$P_1P_2$上利用一阶公式求出点$P_1^{‘}$，最后在$P_0^{‘}P_1^{‘}$上再利用一阶公式就可以求出最终贝塞尔曲线上的点$P_0{”}$。具体推导过程如下：
先求出线段上的控制点：
$$P_0^{‘}=(1-t)P_0+tP_1$$
$$P_1^{‘}=(1-t)P_1+tP_2$$
将上面的公式带入至下列公式中：
$$B_{2}(t)=(1-t)P_0^{‘}+tP_1^{‘}$$
$$=(1-t)((1-t)P_0+tP_1)+t((1-t)P_1+tP_2)$$
$$=(1-t)^2P_0+2t(1-t)P_1+t^2P_2$$
得出以下公式：
$$B_{2}(t)=(1-t)^2P_0+2t(1-t)P_1+t^2P_2,t\in[0,1]$$
上面的推导可能比较抽象，不太能理解。下面我们以实例来讲解：
在平面内任选3个不共线的点，依次用线段连接。
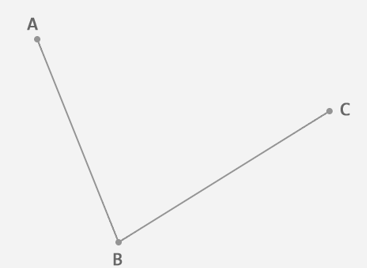
在第一条线段上任选一个点D。计算该点到线段起点的距离AD，与该线段总长AB的比例。
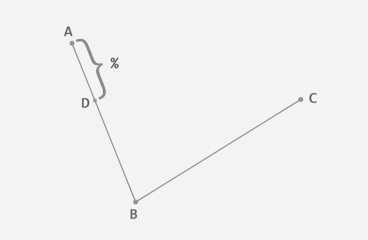
根据上一步得到的比例，从第二条线段上找出对应的点E，使得 AD:AB=BE:BC。
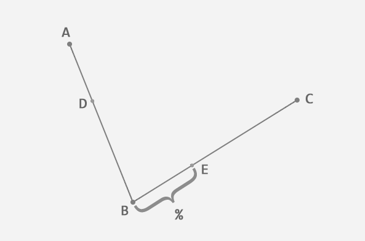
连接这两点DE。
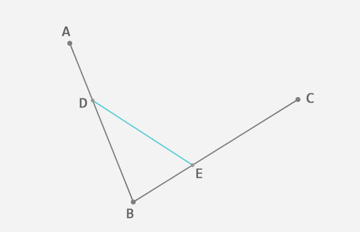
到这里，我们就确定了贝塞尔曲线上的一个点F。接下来，请稍微回想一下极限知识，让选取的点D在第一条线段上从起点A移动到终点B，找出所有的贝塞尔曲线上的点F。所有的点找出来之后，我们也得到了这条贝塞尔曲线。
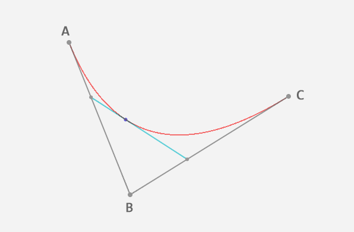
回过头来看这条贝塞尔曲线，为了确定曲线上的一个点，需要进行两轮取点的操作，因此我们称得到的贝塞尔曲线为二次曲线（这样记忆很直观，但曲线的次数其实是由前面提到的伯恩斯坦多项式决定的）。
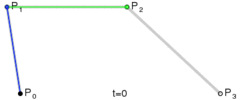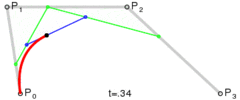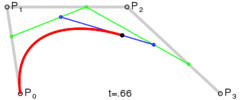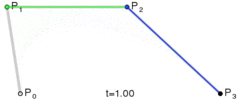
与二阶贝塞尔曲线类似，可以通过相同的方法得出以下坐标公式：
$$B_{3}(t)=(1-t)^3P_0+3t(1-t)^2P_1+3t^2(1-t)P_2+t^3P_3,t\in[0,1]$$
当控制点个数为4时，情况是怎样的？
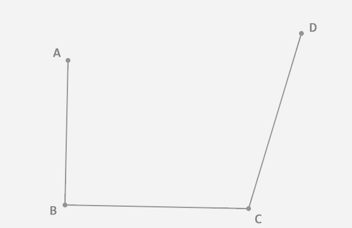
步骤都是相同的，只不过我们每确定一个贝塞尔曲线上的点，要进行三轮取点操作。如图，AE:AB=BF:BC=CG:CD=EH:EF=FI:FG=HJ:HI，其中点J就是最终得到的贝塞尔曲线上的一个点。
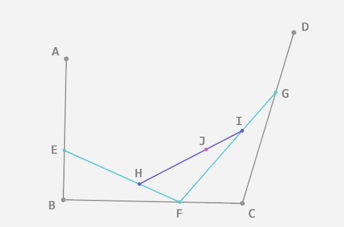这样我们得到的是一条三次贝塞尔曲线。
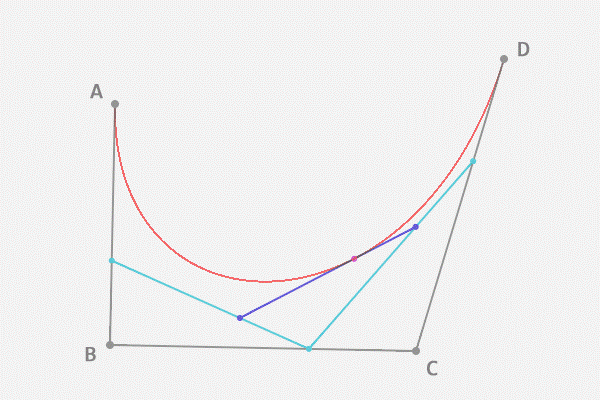
多阶贝塞尔曲线
n阶贝塞尔曲线公式：
$$B(t)=\sum_{i=0}^{n}C_n^{i}P_i(1-t)^{n-i}t^i,t\in[0,1]$$
即：
$$B(t)=\sum_{i=0}^{n}P_ib_{i,n}(t),t\in[0,1]$$
公式中$C_n^i$的值为$\frac{n!}{(n-i)!\cdot i!}$，与统计学有关。
其中$b_{i,n}(t)$的值为：
$$b_{i,n}(t)=C_n^{i}(1-t)^{n-i}t^i,其中i=0,1,…,n$$
什么是样条？
样条从英文spline翻译过来的，由于没有实际参照对象，非常让人费解。B样条的数学定义更是让人匪夷所思。实际应用中，样条是一根富有弹性的细木条或塑料条。在应用CAD/CAM技术以前，航空、船舶和汽车制造业普遍采用手工绘制自由曲线。绘制员用压铁压住样条，使其通过所有给定的型值点，再适当地调整压铁，改变样条形态，直到符合设计要求。所以在绘图术语中，样条是通过一组指定点集而生成平滑曲线的柔性带。样条曲线（splinecurve）原指用这种方式绘制的曲线。
- 从力学角度考虑，样条可看作一弹性细梁，压铁是作用在梁上的集中载荷。由此，设计样条曲线的过程可抽象为：求弹性细梁在外加集中载荷作用下产生的弯曲变形。
- 在数学上使用分段的三次多项式函数来描绘这种曲线，其中各曲线段的连接处有连续的一次和二次导数。
- 在计算机图形学中，样条曲线指由多项式曲线段连接而成的曲线，在每段的边界处满足特定的连续性条件。
什么是B样条？
在学习B样条的知识之前，一定要首先了解Bezier曲线在外形设计的应用中存在一些具体的不足之处：
- 确定了多边形的顶点数（m个），也就决定了所定义的Bezier曲线的阶次（m-1次），这样很不灵活。
- 当顶点数（m）较大时，曲线的阶次将比较高。此时，多边形对曲线形状的控制将明显减弱。
- Bezier的调和函数的值，在开区间（0,1）内均不为0。因此，所定义的曲线在（0<t<1）的区间内的任何一点均要受到全部顶点的影响，即改变其中任一个顶点的位置，都将对整条曲线产生影响，因此对曲线进行局部修改是不可能的。
B样条曲线，简单来说，它是对贝塞尔曲线的一个补充。为什么这样说呢？是因为贝塞尔曲线某些情况下不实用：曲线上每个点受所有控制点影响，这会给调整曲线工作带来麻烦。可以想到的第一个优化是，把整个贝塞尔曲线变成多段贝塞尔子曲线的拼接。然而，这个方案也不好用，因为拼接工作很难做好，因为要拼接曲线显得”光滑”前提是保证相邻曲线之间的连续性。
为了克服以上提到的在Bezier曲线中存在的问题，Gordon、Riesenfeld和Forrest等人拓展了Bezier曲线，用n次B样条基函数替换了伯恩斯坦基函数，构造了B样条曲线。B样条曲线除了保持Bezier曲线所具有的优点外，还增加了可以对曲线进行局部修改这一突出的优点。除此之外，它还具有对特征多边形更逼近以及多项式阶次较低等优点。
B样条是对贝塞尔曲线的一般化。因而，Bezier曲线能表达的，B样条也同样可以。而且，因为B样条引入了控制点个数与曲线阶次无关的特性，使得我们可以对低阶曲线有了更好的控制能力。而且，通过对节点序列的控制，使得我们对曲线有自由的调节能力。因此，B样条曲线在外形设计中得到了更广泛的重视和应用。
与Bezier曲线的定义相似，B样条曲线的定义是：给定n+1个控制点$\{P_0,P_1,…,P_n\}$,m+1个节点$\{u_0,u_1,…,u_m\}$,p阶B样条曲线$C(u)=\sum_{i=0}^nN_{i,p}(u)P_i$。相对Bezier曲线不同之处在于：
- B样条的控制点个数与曲线次数无关，因此B样条的自由度更大，可以定义很多控制点又不用担心曲线次数过高而计算困难。
- B样条有多个节点区间，使得其为分段函数，而Bezier曲线只有一个区间。
B样条取消与赛贝尔曲线的关系
- B样条上任意一个区间$[u_i,u_{i+1})$上的曲线的定义都是一个Bezier。因此可以将B样条转为分段bezier曲线。
- Bezier是一种特殊的样条曲线。
样条及B样条再Python中的使用
样条示例代码：（已废弃）
import numpy as np import matplotlib.pyplot as plt from scipy.interpolate import spline x = range(50) y = [137,17,110,383,477,623,858,1165,1353,1516,2039,1353,2453,1245,2136,1149,1148,894,277,414,399,297,103,102,103,57,54,63,52,27,38,102,14,13,31,38,11,17,51,11,19,14,22,18,29,3,7,6,11,142] x = np.array(x) y = np.array(y) x_smooth = np.linspace(x.min(), x.max(), 1000) y_smooth = spline(x, y, x_smooth) plt.plot(x_smooth, y_smooth) plt.show()
B样条示例代码：
import numpy as np import matplotlib.pyplot as plt from scipy.interpolate import BSpline, splrep x = range(50) y = [137,17,110,383,477,623,858,1165,1353,1516,2039,1353,2453,1245,2136,1149,1148,894,277,414,399, 297,103,102,103,57,54,63,52,27,38,102,14,13,31,38,11,17,51,11,19,14,22,18,29,3,7,6,11, 142] x = np.array(x) y = np.array(y) t, c, k = splrep(x, y, s=0, k=3) x_smooth = np.linspace(x.min(), x.max(), 1000) y_smooth = BSpline(t, c, k, extrapolate=False) plt.plot(x, y, 'ko', label='Original points') plt.plot(x_smooth, y_smooth(x_smooth), 'r', label='BSpline') plt.legend(loc='best') plt.show()
参考链接：
