在精细化运营细分维度的PK中,经常会遇到部分场景下数据量较小导致结构存在偏差的问题。于是引入了贝叶斯平均并发现效果不错。
贝叶斯平均简介
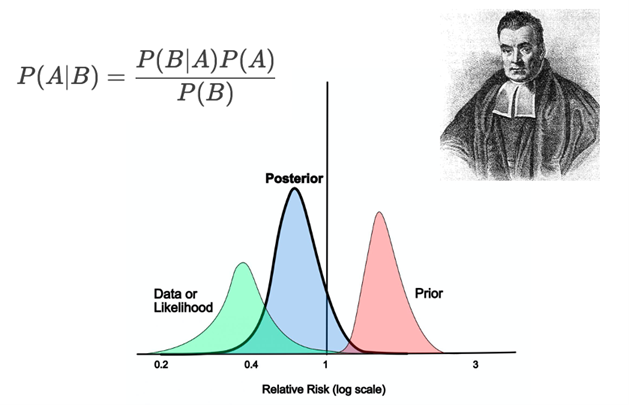
贝叶斯平均(Bayesian Average)是一种结合先验信息与观测数据来估计平均值的统计方法,旨在解决小样本数据下的估计偏差问题。它通过引入先验参数,使得结果在数据量较少时更稳定,随着数据量的增加逐渐趋近于实际平均值。
与算法平均的对比:
| 场景 | 算数平均 | 贝叶斯平均 |
| 样本量极小(如n=1) | 完全依赖单一数据,波动大 | 接近整体平均值,更稳定 |
| 样本量大(如n=1000) | 结果准确 | 几乎等于算术平均 |
| 抗操纵性 | 易受刷分影响 | 虚增样本降低极端值影响 |
核心思想
- 先验与后验的平衡:贝叶斯平均基于贝叶斯统计思想,假设存在一个先验平均值(通常基于全局数据或领域知识),当样本量较小时,结果偏向先验值;随着样本量增大,结果逐渐向实际观测值靠拢。
- 稳健性:避免因数据稀疏导致的极端值(如仅有少数高评分的商品),提升估计的可靠性。
基本原理
贝叶斯平均法的核心思想是:在计算平均值时,引入一个先验的”虚拟数据”作为基准,从而平衡样本量不足导致的极端值影响。例如:
- 小样本问题:一个新商品仅有2个五星评分,算术平均为5分,但这可能高估其真实质量。
- 解决方法:假设所有商品的先验平均评分为3分,并虚拟添加一定数量的”基准评分”(如10个3分),再计算新的加权平均。
数学公式
贝叶斯平均的通用公式为:
$$\text{贝叶斯平均}=\frac{C\cdot m+n\cdot \bar{x}}{C+n}$$
- C:先验样本量(虚拟数据量),控制先验信息的权重。
- m:先验平均值(如整体数据的平均值)。
- n:实际观测的样本量。
- $\bar{x}$:实际观测的平均值。
特点:
- 当n 较小时,结果趋近于先验值 m 。
- 当n 较大时,结果趋近于实际观测值$\bar{x}$ 。
优点与局限
- 优点:
- 减少小样本噪声,估计更可靠。
- 实现简单,计算高效。
- 局限:
- 先验参数($\mu_0$和C)需合理选择,不当设定可能导致偏差。
- 假设先验分布可能与真实情况不符,影响准确性。
贝叶斯平均的应用
在精细化运营中,细分维度的PK(如不同用户群体、产品类别、渠道等之间的效果对比)常面临数据稀疏性和样本偏差问题。贝叶斯平均通过引入全局先验信息,能更公平地比较不同细分维度的表现,避免小样本数据误导决策。
应用逻辑
- 核心目标:在细分维度(如用户分群、商品品类、地区)的对比中,消除数据量差异带来的评估偏差。
- 关键问题:
- 直接使用平均值(如转化率、客单价)可能导致”小样本高波动”维度虚高排名。
- 传统方法(如设定最低样本量阈值)会损失长尾维度的信息。
- 贝叶斯平均的解决方案:
- 为每个细分维度计算“调整后的得分”,结合全局平均(先验)和当前维度实际数据(后验)。
- 数据量少的维度得分向全局均值收缩,数据量大的维度更接近真实值。
应用步骤
步骤1:选择细分维度与指标
- 细分维度:如用户年龄段(18-24岁、25-30岁)、商品类目(服饰、数码)、城市等级(一线、二线)等。
- 评估指标:如转化率、复购率、平均停留时长、客单价等。
步骤2:确定先验参数($\mu_0$和C)
- 全局平均值($\mu_0$):使用全量数据的均值(如全站用户平均转化率)。
- 调节参数(C):控制先验的权重,需结合业务经验调整:
示例:若认为某个细分维度需至少100个样本才可信,可设C=100,即当该维度样本量n=10时,先验权重为100/(100+10)≈90%。
步骤3:计算各维度的贝叶斯平均得分
$$\text{调整后得分}=\frac{C\cdot \mu_0+\sum x_i}{C+n}$$
- $\sum x_i$:该维度的指标总和(如所有用户的转化次数之和)。
- n:该维度的样本量(如用户数、商品数)。
步骤4:基于调整后得分进行PK排名
按调整后得分排序,优先对数据充足且表现优异的维度分配资源。
示例:
- 某小众商品类目(样本量少但转化率高)的得分会被收缩,避免过度推荐;
- 某头部类目(样本量大且转化率高)的得分更可信,资源倾斜更安全。
典型场景示例
场景1:用户分群的活跃度PK
- 目标:对比不同年龄段用户的日均使用时长,决定优先运营哪个人群。
- 问题:新用户群(如18-24岁)样本量少,单日活跃时长波动大。
- 解决方案:
- 计算每个年龄段的贝叶斯平均活跃时长,收缩小样本群组的极端值。
- 优先优化调整后得分高且样本量适中的群体,平衡效果与稳定性。
场景2:商品类目转化率PK
- 目标:对比不同商品类目的转化率,优化首页推荐位资源分配。
- 问题:冷门类目(如”手工艺品”)可能因偶然高转化率被误判为优质类目。
- 解决方案:
- 使用贝叶斯平均调整转化率,冷门类目得分向全站平均转化率(如2%)收缩。
- 资源优先分配给调整后转化率高且样本量大的类目(如”数码3C”)。
场景3:广告渠道的ROI对比
- 目标:评估不同广告渠道(如抖音、微信)的ROI,优化投放预算。
- 问题:新渠道(如小红书)初期投放量小,ROI波动性高。
- 解决方案:
- 用贝叶斯平均计算各渠道ROI,新渠道得分向历史渠道均值靠拢。
- 避免因短期高ROI过度倾斜预算,确保决策稳健性。
参数设定与调优建议
- 全局平均值($\mu_0$):若业务场景复杂(如不同品类差异大),可分层设定(如分品类计算先验均值)。
- 调节参数(C):
- 经验公式:C ≈ 业务认可的“最小可信样本量”(如认为至少50单数据可信,则设 C=50)。
- 调优方法:通过历史数据模拟,选择使排名结果最稳定的 C 值。
- 动态调整:周期性更新 $\mu_0$ 和 C(如每周更新一次),适应业务变化。
优势与注意事项
- 优势
- 公平性:平衡大小样本维度的可比性。
- 资源效率:避免因小样本误判浪费资源。
- 解释性强:公式透明,易于业务方理解。
- 注意事项
- 先验偏差:若全局均值($\mu_0$)与细分维度真实均值差异大,需重新校准。
- 参数敏感性:调节参数 C 需通过 A/B 测试或历史验证选择。
- 数据分层:对异质性强的维度(如不同消费档次的用户),建议分层计算先验。
总结
贝叶斯平均在细分维度 PK 中的应用,本质是通过数据平滑提升对比的可靠性。它尤其适用于以下场景:
- 长尾维度(样本量差异大)的公平比较;
- 冷启动期资源分配(如新品、新渠道);
- 防止过度依赖短期波动数据。
通过合理设定参数,贝叶斯平均能帮助运营者更科学地识别“真正优质”的细分维度,推动精细化策略的落地。