很多参数估计问题均采用似然函数作为目标函数,当训练数据足够多时,可以不断提高模型精度,但是以提高模型复杂度为代价的,同时带来一个机器学习中非常普遍的问题——过拟合。所以,模型选择问题在模型复杂度与模型对数据集描述能力(即似然函数)之间寻求最佳平衡。
人们提出许多信息准则,通过加入模型复杂度的惩罚项来避免过拟合问题,信息准则=复杂度惩罚+精度惩罚,值越小越好。
- 复杂度惩罚:对应”参数数量”、”训练数据量”,数值变大表明模型复杂度增加,容易过拟合
- 精度惩罚:对应”负log-似然函数”,数值变大表明似然函数降低,模型对数据集的描述能力下降
1、实现参数的稀疏有什么好处?
一个好处是可以简化模型、避免过拟合。因为一个模型中真正重要的参数可能并不多,如果考虑所有的参数作用,会引发过拟合。并且参数少了模型的解释能力会变强。
2、参数值越小代表模型越简单吗?
是。越复杂的模型,越是会尝试对所有的样本进行拟合,甚至包括一些异常样本点,这就容易造成在较小的区间里预测值产生较大的波动,这种较大的波动也反应了在这个区间的导数很大,而只有较大的参数值才能产生较大的导数。因此
复杂的模型,其参数值会比较大。
此处我们介绍一下常用的两个模型选择方法——赤池信息准则(Akaike Information Criterion,AIC)和贝叶斯信息准则(Bayesian Information Criterion,BIC)。
AIC
赤池信息量准则(英语:Akaike information criterion,简称AIC)是评估统计模型的复杂度和衡量统计模型”拟合”资料之优良性(Goodness of fit)的一种标准,是由日本统计学家赤池弘次创立和发展的。赤池信息量准则建立在信息熵的概念基础上。
在一般的情况下,AIC可以表示为:
$$AIC=2k-2\ln(L)$$
其中:
- k是参数的数量
- L是似然函数
假设条件是模型的误差服从独立正态分布。让n为观察数,RSS为残差平方和,那么AIC变为:
$$AIC=2k+n\ln(RSS/n)$$
增加自由参数的数目提高了拟合的优良性,AIC鼓励数据拟合的优良性但尽量避免出现过度拟合(Overfitting)的情况。所以优先考虑的模型应是AIC值最小的那一个。赤池信息量准则的方法是寻找可以最好地解释数据但包含最少自由参数的模型。
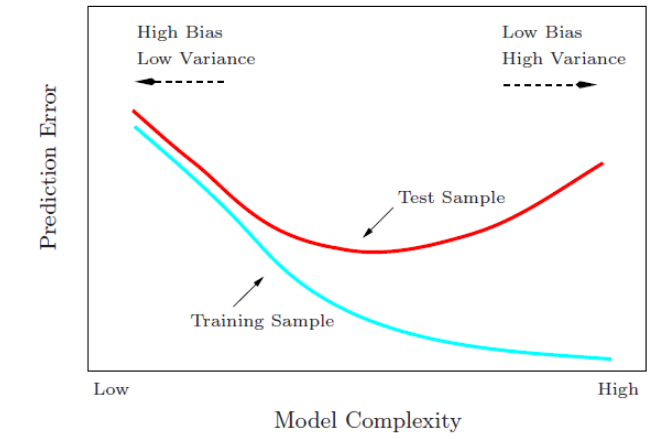
当两个模型之间存在较大差异时,差异主要体现在似然函数项,当似然函数差异不显著时,上式第一项,即模型复杂度则起作用,从而参数个数少的模型是较好的选择。一般而言,当模型复杂度提高(k增大)时,似然函数L也会增大,从而使AIC变小,但是k过大时,似然函数增速减缓,导致AIC增大,模型过于复杂容易造成过拟合现象。AIC不仅要提高模型拟合度(极大似然),而且引入了惩罚项,使模型参数尽可能少,有助于降低过拟合的可能性。
BIC
贝叶斯信息准则,也称为Bayesian Information Criterion(BIC)。贝叶斯决策理论是主观贝叶斯派归纳理论的重要组成部分。是在不完全情报下,对部分未知的状态用主观概率估计,然后用贝叶斯公式对发生概率进行修正,最后再利用期望值和修正概率做出最优决策。公式为:
$$BIC=\ln(n)k-2ln(L)$$
其中,
- k为模型参数个数
- n为样本数量
- L为似然函数
$\ln(n)k$惩罚项在维数过大且训练样本数据相对较少的情况下,可以有效避免出现维度灾难现象。
与AIC相似,训练模型时,增加参数数量,也就是增加模型复杂度,会增大似然函数,但是也会导致过拟合现象,针对该问题,AIC和BIC均引入了与模型参数个数相关的惩罚项,BIC的惩罚项比AIC的大,考虑了样本数量,样本数量过多时,可有效防止模型精度过高造成的模型复杂度过高。
AIC和BIC该如何选择?
AIC和BIC的原理是不同的,AIC是从预测角度,选择一个好的模型用来预测,BIC是从拟合角度,选择一个对现有数据拟合最好的模型,从贝叶斯因子的解释来讲,就是边际似然最大的那个模型。
共性
- 构造这些统计量所遵循的统计思想是一致的,就是在考虑拟合残差的同事,依自变量个数施加”惩罚”。
不同点
- BIC的惩罚项比AIC大,考虑了样本个数,样本数量多,可以防止模型精度过高造成的模型复杂度过高。
- AIC和BIC前半部分是一样的,BIC考虑了样本数量,样本数量过多时,可有效防止模型精度过高造成的模型复杂度过高。
AIC和BIC前半部分是惩罚项,当n≥8n≥8时,kln(n)≥2kkln(n)≥2k,所以,BIC相比AIC在大数据量时对模型参数惩罚得更多,导致BIC更倾向于选择参数少的简单模型。
AIC/BIC实战:Lasso模型选择
本示例利用Akaike信息判据(AIC)、Bayes信息判据(BIC)和交叉验证,来筛选Lasso回归的正则化项参数alpha的最优值。
通过LassoLarsIC得到的结果,是基于AIC/BIC判据的。这种基于信息判据(AIC/BIC)的模型选择非常快,但它依赖于对自由度的正确估计。该方式的假设模型必需是正确,而且是对大样本(渐近结果)进行推导,即,数据实际上是由该模型生成的。当问题的背景条件很差时(特征数大于样本数),该模型选择方式会崩溃。
对于交叉验证,我们使用20-fold的2种算法来计算Lasso路径:LassoCV类实现的坐标下降和LassoLarsCV类实现的最小角度回归(Lars)。这两种算法给出的结果大致相同,但它们在执行速度和数值误差来源方面有所不同。
Lars仅为路径中的每个拐点计算路径解决方案。因此,当只有很少的弯折时,也就是很少的特征或样本时,它是非常有效的。此外,它能够计算完整的路径,而不需要设置任何元参数。与之相反,坐标下降算法计算预先指定的网格上的路径点(本示例中我们使用缺省值)。因此,如果网格点的数量小于路径中的拐点的数量,则效率更高。如果特征数量非常大,并且有足够的样本来选择大量特征,那么这种策略就非常有趣。在数值误差方面,Lars会因变量间的高相关度而积累更多的误差,而坐标下降算法只会采样网格上路径。
注意观察alpha的最优值是如何随着每个fold而变化。这是为什么当估交叉验证选择参数的方法的性能时,需要使用嵌套交叉验证的原因:这种参数的选择对于不可见数据可能不是最优的。
import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoCV, LassoLarsCV, LassoLarsIC
from sklearn import datasets
# 这样做是为了避免在 np.log10 时除零
EPSILON = 1e-4
diabetes = datasets.load_diabetes()
X = diabetes.data
y = diabetes.target
rng = np.random.RandomState(42)
X = np.c_[X, rng.randn(X.shape[0], 14)] # 添加一些不好的特征
# 将最小角度回归得到的数据标准化,以便进行比较
X /= np.sqrt(np.sum(X**2, axis=0))
# LassoLarsIC: 用 BIC/AIC 判据进行最小角度回归
model_bic = LassoLarsIC(criterion='bic')
t1 = time.time()
model_bic.fit(X, y)
t_bic = time.time() - t1
alpha_bic_ = model_bic.alpha_
model_aic = LassoLarsIC(criterion='aic')
model_aic.fit(X, y)
alpha_aic_ = model_aic.alpha_
def plot_ic_criterion(model, name, color):
alpha_ = model.alpha_ + EPSILON
alphas_ = model.alphas_ + EPSILON
criterion_ = model.criterion_
plt.plot(-np.log10(alphas_), criterion_, '--', color=color,
linewidth=3, label='%s 判据' % name)
plt.axvline(-np.log10(alpha_), color=color, linewidth=3,
label='alpha: %s 估计' % name)
plt.xlabel('-log(alpha)')
plt.ylabel('判据')
plt.figure()
plot_ic_criterion(model_aic, 'AIC', 'b')
plot_ic_criterion(model_bic, 'BIC', 'r')
plt.legend()
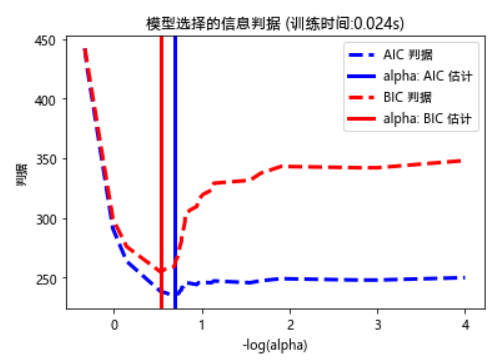
plt.title('模型选择的信息判据 (训练时间: %.3fs)' % t_bic)
plt.show()
import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoCV, LassoLarsCV, LassoLarsIC
from sklearn import datasets
# 这样做是为了避免在 np.log10 时除零
EPSILON = 1e-4
diabetes = datasets.load_diabetes()
X = diabetes.data
y = diabetes.target
rng = np.random.RandomState(42)
X = np.c_[X, rng.randn(X.shape[0], 14)] # 添加一些不好的特征
# 将最小角度回归得到的数据标准化,以便进行比较
X /= np.sqrt(np.sum(X**2, axis=0))
# LassoLarsIC: 用 BIC/AIC 判据进行最小角度回归
model_bic = LassoLarsIC(criterion='bic')
t1 = time.time()
model_bic.fit(X, y)
t_bic = time.time() - t1
alpha_bic_ = model_bic.alpha_
model_aic = LassoLarsIC(criterion='aic')
model_aic.fit(X, y)
alpha_aic_ = model_aic.alpha_
# LassoCV: 坐标下降
# 计算路径
t1 = time.time()
model = LassoCV(cv=20).fit(X, y)
t_lasso_cv = time.time() - t1
# 显示结果
m_log_alphas = -np.log10(model.alphas_ + EPSILON)
plt.figure()
ymin, ymax = 2300, 3800
plt.plot(m_log_alphas, model.mse_path_, ':')
plt.plot(m_log_alphas, model.mse_path_.mean(axis=-1), 'k',
label='平均', linewidth=2)
plt.axvline(-np.log10(model.alpha_ + EPSILON), linestyle='--', color='k',
label='alpha: CV 估计')
plt.legend()
plt.xlabel('-log(alpha)')
plt.ylabel('均方惨差')
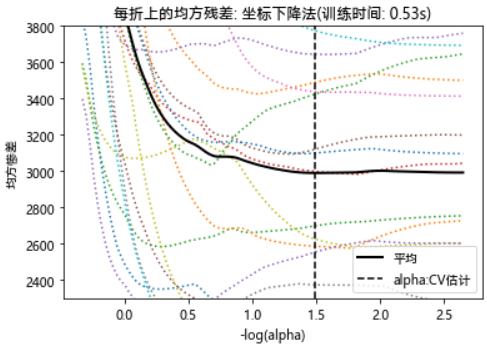
plt.title('每折上的均方残差: 坐标下降法'
'(训练时间: %.2fs)' % t_lasso_cv)
plt.axis('tight')
plt.ylim(ymin, ymax)
plt.show()
import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoCV, LassoLarsCV, LassoLarsIC
from sklearn import datasets
# 这样做是为了避免在 np.log10 时除零
EPSILON = 1e-4
diabetes = datasets.load_diabetes()
X = diabetes.data
y = diabetes.target
rng = np.random.RandomState(42)
X = np.c_[X, rng.randn(X.shape[0], 14)] # 添加一些不好的特征
# 将最小角度回归得到的数据标准化,以便进行比较
X /= np.sqrt(np.sum(X**2, axis=0))
# LassoLarsIC: 用 BIC/AIC 判据进行最小角度回归
model_bic = LassoLarsIC(criterion='bic')
t1 = time.time()
model_bic.fit(X, y)
t_bic = time.time() - t1
alpha_bic_ = model_bic.alpha_
model_aic = LassoLarsIC(criterion='aic')
model_aic.fit(X, y)
alpha_aic_ = model_aic.alpha_
ymin, ymax = 2300, 3800
# LassoLarsCV: 最小角度回归法
# Compute paths
print("Computing regularization path using the Lars lasso...")
t1 = time.time()
model = LassoLarsCV(cv=20).fit(X, y)
t_lasso_lars_cv = time.time() - t1
# Display results
m_log_alphas = -np.log10(model.cv_alphas_ + EPSILON)
plt.figure()
plt.plot(m_log_alphas, model.mse_path_, ':')
plt.plot(m_log_alphas, model.mse_path_.mean(axis=-1), 'k',
label='平均', linewidth=2)
plt.axvline(-np.log10(model.alpha_), linestyle='--', color='k',
label='alphaCV')
plt.legend()
plt.xlabel('-log(alpha)')
plt.ylabel('均方惨差')
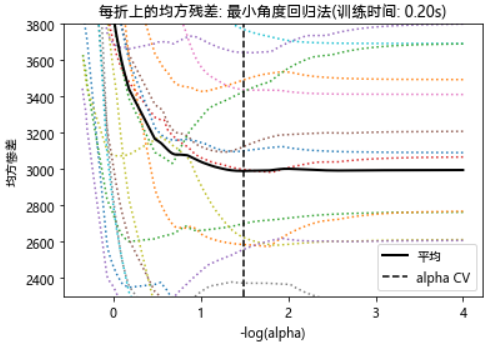
plt.title('每折上的均方残差: 最小角度回归法'
'(训练时间: %.2fs)' % t_lasso_lars_cv)
plt.axis('tight')
plt.ylim(ymin, ymax)
plt.show()
参考链接:




讲的很清楚,还有实例,感谢
aic, bic 准则 lr模型,决策树模型 怎么用呢?