Adtributor算法简介
Adtributor算法是由微软研究院在2014年提出的一种用于多维时间序列异常根因分析的方法。它主要用于解决以下问题:当某个关键性能指标(KPI)发生异常波动时,如何快速准确地找出导致该异常的根本原因。尤其适用于复杂的多维度数据场景。
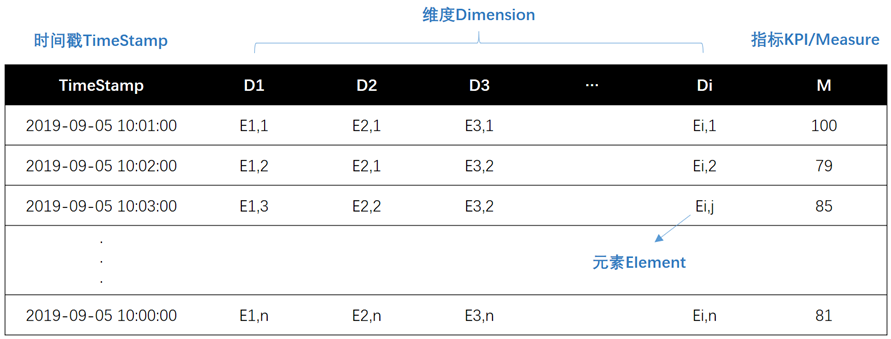
举个例子,假设一个电商平台的日订单量突然下降,导致订单量下降的原因可能有多种,例如:
- 时间维度:促销活动结束、节假日影响等。
- 地区维度:某个或某些地区的订单量大幅下降。
- 渠道维度:某个或某些推广渠道的效果变差。
- 商品维度:某个或某些商品的销量大幅下滑。
Adtributor算法能够自动分析这些多维度的数据,找出导致订单量下降的根本原因。
原始论文:《Adtributor: Revenue Debugging in Advertising Systems》
核心思想
Adtributor算法基于以下两个核心概念来量化根因:
- 解释力(Explanatory Power, EP):指某个维度或维度内的某个元素对于KPI异常的解释程度。EP越高,说明该维度或元素越有可能是导致异常的根本原因。
- 惊奇性(Surprise, S):指某个维度或维度内的某个元素的异常程度。S越高,说明该维度或元素的变化越显著。
Adtributor算法假设所有根因都是一维的,通过计算每个维度的惊奇性(维度内所有元素惊奇性之和)对维度进行排序,从而确定根因所在的维度。然后,再通过分析该维度内各个元素的解释力和惊奇性,找出最终的根因。

数学解释
Adtributor算法的核心在于量化”解释力(Explanatory Power, EP)”和”惊奇性(Surprise, S)”,并通过这两个指标来定位异常的根因。
数据预处理和异常检测
首先,我们需要收集KPI的多维时间序列数据,并进行必要的预处理,例如数据清洗、缺失值填充等。然后,使用时间序列模型(例如ARMA模型)对KPI进行预测。
假设我们要分析的KPI为m,时间点为t。
- 模型预测值:$F_t(m)$
- 实际值:$A_t(m)$
- 异常程度(绝对偏差):$|A_t(m)-F_t(m)|$
解释力(Explanatory Power, EP)
解释力(EP)用于衡量某个维度或维度内的某个元素对于KPI异常的解释程度。
假设我们需要分析d个维度,每个维度i有$n_i$个元素。对于维度i中的元素j,其EP值计算公式如下:
$$EP_{ij}(m)=\frac{A_{ij}(m)-F_{ij}(m)}{A_t(m)-F_t(m)}\times100%$$
其中:
- $A_{ij}(m)$:维度i的元素j上KPI m的实际值。
- $F_{ij}(m)$:维度i的元素j上KPI m的预测值。
- $A_t(m)$:KPI m的总体实际值。
- $F_t(m)$:KPI m的总体预测值。
这个公式的含义是,元素j的异常变化占KPI总体异常变化的百分比。EP值可以是正数、负数或大于100%。需要注意的是,同一维度下所有元素的EP值之和必须为100%。
惊奇性(Surprise, S)
惊奇性(S)用于衡量某个维度或维度内的某个元素的异常程度。Adtributor算法使用以下公式计算维度i中元素j的惊奇性:
$$S_{ij}(m)=|(A_{ij}(m)–F_{ij}(m))/F_{ij}(m)|$$
这个公式计算的是元素j的实际值与预测值之间的相对偏差的绝对值。S值越高,说明该元素的变化越显著,越”令人惊讶”。
对于整个维度i,其惊奇性定义为该维度下所有元素的惊奇性之和:
$$S_{i}(m)=\sum_{j=1}^{n_i}S_{ij}(m)$$
补充说明:EP和S的正负号及特殊情况
- EP的正负号:
- 如果$A_{ij}(m)>F_{ij}(m)$且$A_t(m)>F_t(m)$,则$EP_{ij}(m)>0$,表示该元素的变化方向与总体变化方向一致,对异常起促进作用。
- 如果$A_{ij}(m)<F_{ij}(m)$且$A_t(m)<F_t(m)$,则$EP_{ij}(m)>0$,同样表示该元素的变化方向与总体变化方向一致,对异常起促进作用。
- 如果$A_{ij}(m)>F_{ij}(m)$且$A_t(m)<F_t(m)$,或$A_{ij}(m)<F_{ij}(m)$且$A_t(m)>F_t(m)$,则$EP_{ij}(m)<0$,表示该元素的变化方向与总体变化方向相反,对异常起抑制作用。
- EP大于100%的情况:
- 如果某个元素的变化幅度远超总体变化幅度,其EP值可能大于100%。例如,如果总体下降了100,而某个元素单独就下降了150,那么该元素的EP值就是150%。这种情况表明该元素对异常的贡献非常大。
- F_{ij}(m)=0的情况:
- 当$F_{ij}(m)=0$时,$S_{ij}(m)$的计算公式会产生除以零的错误。实际应用中,通常会设置一个很小的正数ε来代替0,即:
- $S_{ij}(m)=\left|\frac{A_{ij}(m)-F_{ij}(m)}{max(F_{ij}(m),\epsilon)}\right|$,其中ε是一个接近于0的正数,例如1e-6。
根因分析
Adtributor算法假设所有根因都是一维的。首先,根据每个维度的惊奇性$S_{i}(m)$对所有维度进行排序,选择惊奇性最高的维度作为潜在的根因维度。
然后,在该维度内,根据每个元素的解释力$EP_{ij}(m)$和惊奇性$S_{ij}(m)$进行分析,找出最有可能的根因元素。通常来说,EP值绝对值较高且S值较高的元素更有可能是根因。
举例说明
假设某电商平台日订单量(KPI m)突然下降了1000单。我们分析了两个维度:地区(维度1)和商品类别(维度2)。
- 地区维度:包括北京、上海、广州三个元素。
- 商品类别维度:包括服装、数码、家居三个元素。
经过计算,得到以下结果:
| 维度 | 元素 | EP(%) | S |
| 地区 | 北京 | 60 | 0.2 |
| 地区 | 上海 | 30 | 0.1 |
| 地区 | 广州 | 10 | 0.05 |
| 商品类别 | 服装 | 40 | 0.5 |
| 商品类别 | 数码 | 30 | 0.4 |
| 商品类别 | 家居 | 30 | 0.1 |
根据维度惊奇性$S_{i}(m)$,商品类别维度(S=0.5+0.4+0.1=1.0)高于地区维度(S=0.2+0.1+0.05=0.35),因此我们首先关注商品类别维度。
在商品类别维度中,服装类别的EP值最高(40%)且S值也较高(0.5),因此我们认为服装类别是导致订单量下降的主要原因。
Adtributor算法的局限
- 根因解释局限于单个维度:未能充分考虑多维度的组合效应。
- 对整体KPI变化情况的严重依赖:在整体KPI变化不大但内部波动剧烈的数据集上表现不佳。
- 难以考虑因素之间的关联关系:算法倾向于在单一维度内寻找原因,忽略了不同因素之间的相互作用。
Adtributor算法的Python实现
Adtributor算法的Python实现涉及多个步骤,包括数据预处理、异常检测、EP和S的计算以及根因分析。由于Adtributor并非一个标准的Python库,因此需要自己编写代码来实现。
初版代码
import pandas as pd
from typing import List, Optional
def calculate_ep_s(
df: pd.DataFrame,
kpi_col: str = "kpi",
prev_kpi_col: str = "prev_kpi",
dim_cols: Optional[List[str]] = None,
) -> pd.DataFrame:
"""计算各维度的EP(贡献度)和S(惊奇性)指标
Args:
df: 包含KPI指标和维度列的原始数据
kpi_col: 当期KPI列名,默认为'kpi'
prev_kpi_col: 前期KPI列名,默认为'prev_kpi'
dim_cols: 需要分析的维度列列表,默认为['dim1', 'dim2']
Returns:
包含各维度值EP和S指标的DataFrame
"""
# 初始化维度列参数
dim_cols = dim_cols or ["dim1", "dim2"]
# 计算KPI变化量
df["change"] = df[kpi_col] - df[prev_kpi_col]
total_change = df["change"].sum()
ep_s_data = []
for dim in dim_cols:
for value in df[dim].unique():
dim_df = df[df[dim] == value]
dim_change = dim_df["change"].sum()
dim_prev_kpi = dim_df[prev_kpi_col].mean()
# 处理除零异常
if dim_prev_kpi == 0:
dim_prev_kpi = 1e-6
# 计算EP指标(贡献度)
ep = (dim_change / total_change * 100) if total_change != 0 else 0
# 计算S指标(惊奇性)
s = abs(dim_change / dim_prev_kpi)
ep_s_data.append({
"dimension": dim,
"value": value,
"EP": round(ep, 2), # 保留两位小数
"S": round(s, 4) # 保留四位小数
})
return pd.DataFrame(ep_s_data)
if __name__ == "__main__":
# 数据加载
raw_df = pd.read_csv("test.csv")
# 计算指标
ep_s_df = calculate_ep_s(raw_df)
# 根因分析
print("\n== 维度惊奇性排序 ==")
dim_s_rank = ep_s_df.groupby("dimension")["S"].sum().sort_values(ascending=False)
print(dim_s_rank.to_markdown(tablefmt="github"), end="\n\n")
# 选取TOP维度分析
top_dim = dim_s_rank.index[0]
print(f"== {top_dim} 维度详细分析 ==")
top_dim_df = (
ep_s_df[ep_s_df["dimension"] == top_dim]
.sort_values(by=["EP", "S"], ascending=False)
.reset_index(drop=True)
)
print(top_dim_df.to_markdown(index=False, tablefmt="github"))
关键改进和注意事项
- 异常检测:上例中使用的是简单周同比。在实际应用中,应根据数据特性选择更合适的异常检测方法,例如时间序列模型(ARIMA、Prophet等)。
- 处理0值:在计算S值时,要特别注意分母为0的情况,避免除零错误。通常的做法是添加一个极小值epsilon。
- 多重根因:原始的Adtributor算法假设只有一个根因。实际情况可能存在多个根因。需要对算法进行扩展以支持多重根因的分析。例如,可以迭代地应用Adtributor算法,每次找到一个根因后将其影响移除,然后再次分析剩余的异常。
- JS散度:一些资料中提到Adtributor使用JS散度来衡量差异性。在实际应用中,直接使用相对偏差或绝对偏差通常也足够有效,并且计算更简单。
- 阈值的使用:一些资料中提到TEP和TEEP阈值。TEP阈值用于判断该维度下的解释力总和是否足够解释该异常。TEEP阈值用于筛选出高解释度的元素。可以根据实际需要添加。
JS散度
S散度(Jensen-Shannon Divergence)是一种衡量两个概率分布之间差异性的度量方式。它是基于KL散度(Kullback-Leibler Divergence)的改进版本,克服了KL散度的一些缺点。
KL散度的不足
- 不对称性:KL(P||Q)不等于KL(Q||P),这意味着使用KL散度衡量P和Q的差异与衡量Q和P的差异结果可能不同。
- 未定义性:当P(x)=0但Q(x)≠0时,KL散度会无穷大,导致无法计算。
JS散度的定义
JS散度定义为P和Q的平均分布与P和Q之间KL散度的平均值:JS(P||Q)=(1/2)*KL(P||M)+(1/2)*KL(Q||M)
其中M是P和Q的平均分布:M=(1/2)*(P+Q)
JS散度的优点
- 对称性:JS(P||Q)=JS(Q||P),克服了KL散度不对称的缺点。
- 有界性:JS散度的取值范围为[0,1],克服了KL散度可能无穷大的问题。当两个分布完全相同时,JS散度为0;当两个分布完全不同时,JS散度为1。
- 更平滑:相比KL散度,JS散度更加平滑,这在一些机器学习任务中是有利的。
JS散度的应用
JS散度广泛应用于机器学习、深度学习等领域,例如:
- 生成对抗网络(GAN):GAN的训练目标是最小化生成分布和真实分布之间的差异,JS散度可以作为一种衡量这种差异的度量方式。
- 文本相似度:JS散度可以用于衡量两个文本的概率分布之间的差异,从而判断文本的相似度。
- 聚类分析:JS散度可以用于衡量不同簇之间的差异,从而进行聚类分析。
与其他度量的比较:
- KL散度:JS散度是KL散度的改进版本,克服了KL散度的不对称性和未定义性。
- Wasserstein距离:Wasserstein距离(Earth Mover’s Distance)相比JS散度,在两个分布没有重叠或重叠很少的情况下,仍然能反映两个分布的远近,而JS散度可能为常量。但在计算复杂度上,Wasserstein距离通常比JS散度更高。
TEP阈值
TEP阈值(Threshold for Explained Proportion)主要应用于异常检测和根因分析领域,尤其是在需要解释KPI(Key Performance Indicator,关键绩效指标)异常波动的原因时。它衡量的是一组因素(或维度)能够解释KPI异常变动的程度。简单来说,TEP阈值设定了一个标准,只有当某些因素能够解释KPI异常变动的一定比例时,这些因素才会被认为是潜在的根因。
TEP阈值的意义和作用:
- 筛选关键因素:在复杂的系统中,导致KPI异常变动的因素可能有很多。TEP阈值可以帮助我们筛选出那些能够对异常做出显著解释的关键因素,从而缩小排查范围,提高效率。
- 量化解释能力:TEP阈值提供了一种量化指标,用于衡量一组因素对KPI异常变动的解释能力。通过设定不同的TEP阈值,我们可以调整分析的灵敏度,平衡误报和漏报的风险。
- 指导根因分析:通过比较不同因素组合的解释比例与TEP阈值,我们可以判断哪些因素最有可能是导致KPI异常的根本原因,从而指导后续的根因分析工作。
TEP阈值的设定:TEP阈值通常设定在0到1之间。
- 较高的TEP阈值(例如8或0.9):表示我们希望根因集合能够尽可能多地解释KPI的异常原因。这意味着只有当一组因素能够解释KPI异常变动的很大一部分时,这些因素才会被认为是潜在的根因。这种设定可以减少误报,但可能会漏掉一些解释力较弱但仍然重要的因素。
- 较低的TEP阈值(例如5或0.6):表示我们允许根因集合解释KPI异常变动的一部分即可。这种设定可以减少漏报,但可能会增加误报,需要进一步的分析来确认真正的根因。
TEP阈值的具体设定需要根据实际的应用场景和数据特点进行调整。一般来说,如果对异常解释的要求较高,或者误报的代价较高,则应该选择较高的TEP阈值;反之,如果对漏报的容忍度较低,则可以选择较低的TEP阈值。
举例说明:
假设某个电商平台的日销售额(KPI)突然下降了10%。我们通过分析发现,以下因素可能与销售额下降有关:
- 因素A:移动端访问量下降5%,导致销售额下降3%。
- 因素B:促销活动力度减弱,导致销售额下降6%。
- 因素C:竞争对手推出新的促销活动,导致销售额下降1%。
如果我们设定TEP阈值为0.7,那么只有因素A和因素B的组合(解释了9%的销售额下降,超过了70%的总下降)才会被认为是潜在的根因。而单独的因素A、因素B或因素C都无法达到TEP阈值。
TEEP阈值
TEEP (Threshold for Explained Element Proportion)阈值针对的是元素而言,用于筛选出在维度中具有高解释度的元素。它的作用是:在一个维度内,只保留那些对KPI异常波动解释力足够强的元素,排除那些影响较小的元素,从而缩小分析范围,提高效率。
TEEP阈值的具体作用:
- 筛选高解释度元素:TEEP阈值设定了一个解释力度的下限。只有当一个元素对KPI异常变动的解释比例超过TEEP阈值时,该元素才会被认为是“可疑元素”,并被纳入该维度的根因集合中。
- 降低噪声干扰:在实际应用中,很多因素可能对KPI产生微小的影响,但这些影响通常是随机的、不重要的“噪声”。TEEP阈值可以有效地过滤掉这些噪声,只关注那些真正对异常波动有显著影响的因素。
- 提高分析效率:通过减少需要分析的元素数量,TEEP阈值可以显著提高根因分析的效率,尤其是在维度包含大量元素的情况下。
TEEP阈值的设定:
TEEP阈值通常设定为一个较小的值,例如1%、2%或5%。这个值的具体选择取决于以下因素:
- KPI异常波动的幅度:如果KPI的异常波动幅度较大,可以适当提高TEEP阈值;反之,如果波动幅度较小,则应降低TEEP阈值,以避免遗漏重要的元素。
- 数据噪声的程度:如果数据中噪声较多,可以适当提高TEEP阈值,以过滤掉更多的噪声;反之,如果数据质量较高,则可以降低TEEP阈值。
- 分析的精细程度:如果需要进行更精细的分析,可以降低TEEP阈值,以保留更多的元素;反之,如果只需要找到主要的根因,则可以提高TEEP阈值。
举例说明:
假设我们分析某个电商平台的订单量下降问题,其中一个维度是“推广渠道”,包含以下元素:
- 搜索引擎推广:导致订单量下降8%。
- 社交媒体推广:导致订单量下降5%。
- 邮件推广:导致订单量下降1%。
- 合作伙伴推广:导致订单量下降5%。
如果我们设定TEEP阈值为2%,那么只有“搜索引擎推广”和“社交媒体推广”这两个元素会被认为是可疑元素,并被纳入“推广渠道”维度的根因集合中。“邮件推广”和“合作伙伴推广”由于解释力低于TEEP阈值,将被排除。
与TEP阈值的配合使用:
TEEP阈值用于在维度内部筛选元素,而TEP阈值用于判断维度整体是否重要。两者结合使用,可以有效地进行多维根因分析:
- 首先,使用TEEP阈值在每个维度内筛选出高解释度的元素,形成每个维度的根因集合。
- 然后,计算每个维度根因集合的解释力总和,并与TEP阈值进行比较,筛选出重要的维度。
通过这种方式,Adtributor算法可以有效地定位导致KPI异常波动的关键因素和关键维度,从而帮助用户快速找到根本原因。
迭代后的代码
import numpy as np
import pandas as pd
from scipy.stats import wasserstein_distance
from typing import List, Optional, Dict, Union
def js_divergence(p: np.ndarray, q: np.ndarray) -> float:
"""计算两个分布的Jensen-Shannon散度
Args:
p: 第一个概率分布
q: 第二个概率分布
Returns:
标准化后的JS散度值
"""
# 计算平均分布
m = (p + q) / 2
# 计算KL散度
kl_p = np.sum(np.where(p != 0, p * np.log(p / m), 0))
kl_q = np.sum(np.where(q != 0, q * np.log(q / m), 0))
return (kl_p + kl_q) / 2
def calculate_ep_s(
df: pd.DataFrame,
kpi_col: str = "kpi",
prev_kpi_col: str = "prev_kpi",
dim_cols: Optional[List[str]] = None,
use_js: bool = True,
) -> pd.DataFrame:
"""计算各维度指标的EP(贡献度)和S(分布差异)
Args:
df: 包含KPI指标的原始数据
kpi_col: 当期KPI列名,默认为'kpi'
prev_kpi_col: 前期KPI列名,默认为'prev_kpi'
dim_cols: 分析维度列列表,默认为['dim1', 'dim2']
use_js: 是否使用JS散度计算S值,默认为True
Returns:
包含各维度EP和S指标的DataFrame
"""
# 初始化维度列
dim_cols = dim_cols or ["dim1", "dim2"]
# 计算KPI变化量
df["change"] = df[kpi_col] - df[prev_kpi_col]
total_change = df["change"].sum()
results = []
for dimension in dim_cols:
for dim_value in df[dimension].unique():
# 获取维度子集
subset = df[df[dimension] == dim_value]
dim_change = subset["change"].sum()
# 计算EP指标
ep = (dim_change / total_change * 100) if total_change != 0 else 0
# 计算S指标
if use_js:
# 归一化概率分布
p = subset[kpi_col].values
q = df[kpi_col].values
# 处理零概率分布
p_norm = p / p.sum() if p.sum() > 0 else np.ones_like(p)/len(p)
q_norm = q / q.sum() if q.sum() > 0 else np.ones_like(q)/len(q)
s = js_divergence(p_norm, q_norm)
else:
# 原始S值计算
prev_kpi_mean = subset[prev_kpi_col].mean() or 1e-6 # 处理零值
s = abs(dim_change / prev_kpi_mean)
results.append({
"dimension": dimension,
"value": dim_value,
"EP": round(ep, 2),
"S": round(s, 4)
})
return pd.DataFrame(results)
def root_cause_analysis(
ep_s_df: pd.DataFrame,
tep_threshold: float = 50.0,
teep_threshold: float = 5.0
) -> List[str]:
"""执行根因分析并返回重要维度
Args:
ep_s_df: 包含EP和S指标的DataFrame
tep_threshold: 维度总EP阈值,默认50%
teep_threshold: 元素EP阈值,默认5%
Returns:
超过阈值的重要维度列表
"""
# 按维度计算总S值排序
dim_ranking = (
ep_s_df.groupby("dimension")["S"]
.sum()
.sort_values(ascending=False)
)
print("\n=== 维度惊奇性排序 ===")
print(dim_ranking.to_markdown(tablefmt="github"))
significant_dims = []
for dim in dim_ranking.index:
dim_data = ep_s_df[ep_s_df["dimension"] == dim]
total_ep = dim_data["EP"].abs().sum()
# TEP阈值判断
if total_ep >= tep_threshold:
significant_dims.append(dim)
print(f"\n维度 {dim} 总EP ({total_ep:.2f}%) 超过阈值 {tep_threshold}%")
# 筛选显著元素
significant_elements = dim_data[
dim_data["EP"].abs() >= teep_threshold
].sort_values(by=["EP", "S"], ascending=False)
if not significant_elements.empty:
print(f"\n{dim} 维度显著元素 (EP ≥ {teep_threshold}%):")
print(significant_elements.to_markdown(index=False, tablefmt="github"))
else:
print(f"{dim} 维度无元素超过TEEP阈值")
if not significant_dims:
print("\n警告:没有维度超过TEP阈值")
return significant_dims
if __name__ == "__main__":
# 数据准备
data = pd.read_csv("test.csv")
# 指标计算(使用JS散度)
analysis_df = calculate_ep_s(data, use_js=True)
# 执行根因分析
print("\n=== 根因分析开始 ===")
important_dims = root_cause_analysis(
analysis_df,
tep_threshold=10.0,
teep_threshold=2.0
)
print("\n=== 分析结果 ===")
print("重要维度:", important_dims)



