A/B测试是我们在日常工作中经常使用的工具,A/B测试的核心就是:确定两个元素或版本(A和B)哪个版本更好,你需要同时实验两个版本。最后,选择最好的版本使用。
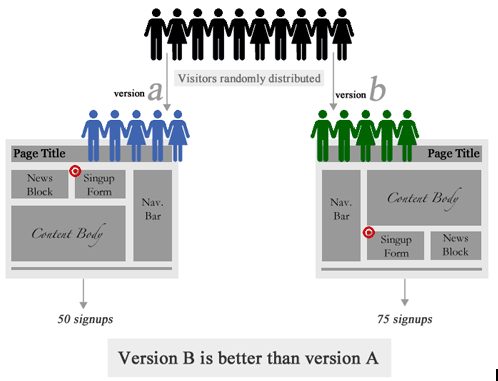
A/B比较困难的点是确定在什么时候可以终止实验。当样本量不够时,监测的“转化率”变化数据可能是由于样本的不均匀导致的。 原则上实现的时间越长,样本量越大,实验的可靠性越高。但是实际过程中我们期望样本量越少越好,如果能提前知道实验结果,则可以快速的进行的版本切换,而不会浪费流量。这就涉及到如何计算实验的最小样本量。比较简单的是使用现成的工具:Evan’s Awesome A/B Tools
样本量计算器功能简介
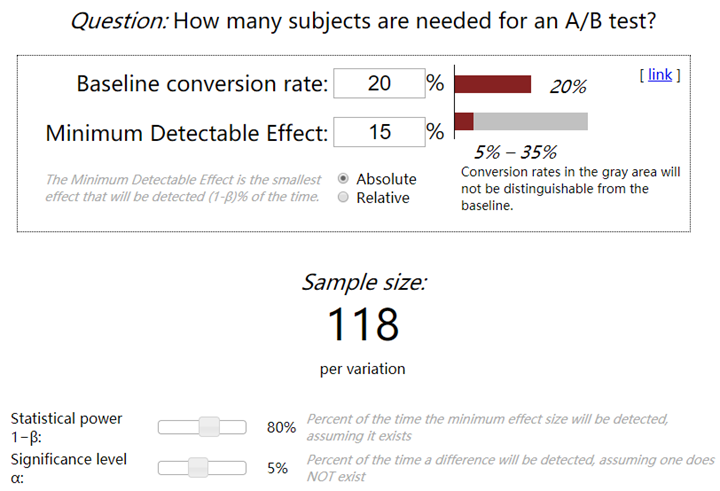
上图为日常使用到的样本计算器的截图,中间主要涉及到的设置项:
- Baseline conversion rate(BCVR):原始版本转化率
- Minimum Detectable Effect(MDE):最小可探测效应(需要监测的转化率效果)
- Absolute:绝对比例,BCVR±MDE
- Relative:相对比例,BCVR*(1±MDE)
- Statistical power $1-\beta$:检验效能Power,也有人称之为把握度,一般选8(即II型错误$\beta=0.2$)或0.9,检验效能越大,需要的样本量越多。
- Significance level $\alpha$:检验水准,临床试验中,检验水准$\alpha$一般取05(双侧检验)或0.025(单侧检验)
上面涉及到的很多概念不是很清晰?特别是$1-\beta$和$\alpha$,不要紧,后面会详细讲解。
样本量计算器原理说明
大数定律
在数学与统计学中,大数定律又称大数法则、大数律,是描述相当多次数重复实验的结果的定律。根据这个定律知道,样本数量越多,则其算术平均值就有越高的概率接近期望值。
大数定律很重要,因为它“说明”了一些随机事件的均值的长期稳定性。人们发现,在重复试验中,随着试验次数的增加,事件发生的频率趋于一个稳定值;人们同时也发现,在对物理量的测量实践中,测定值的算术平均也具有稳定性。比如,我们向上抛一枚硬币,硬币落下后哪一面朝上是偶然的,但当我们上抛硬币的次数足够多后,达到上万次甚至几十万几百万次以后,我们就会发现,硬币每一面向上的次数约占总次数的二分之一,亦即偶然之中包含着必然。
中心极限定理
中心极限定理(Central limit theorem, 简作CLT)是概率论中的一组定理。中心极限定理说明,在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布。这组定理是数理统计学和误差分析的理论基础,指出了大量随机变量之和近似服从正态分布的条件。
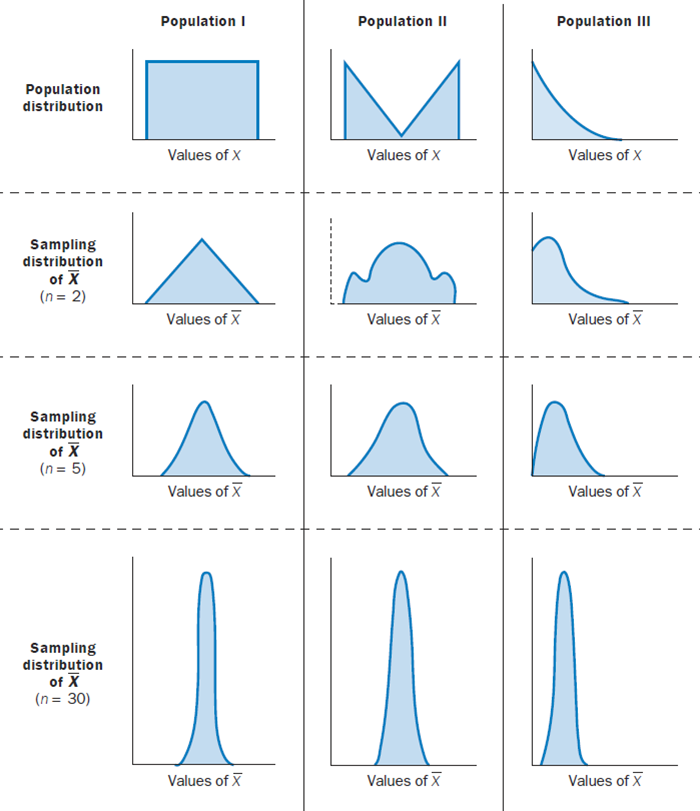
根据大数定律和中心极限定理,当样本量较大(大于30)时,可以通过Z检验来检验测试组和对照组两个样本均值差异的显著性。注:样本量小于30时,可进行t检验。
假设检验
假设检验是依据反证法思想,首先对总体参数提出某种假设(原假设),然后利用样本信息去判断这个假设是否成立的过程。在A/B Test中一般有两种假设:
- 原假设H0:我们反对的假设(样本与总体或样本与样本间的差异是由抽样误差引起的)
- 备择假设H1:我们坚持的假设(样本与总体或样本与样本间存在本质差异)
假设检验的目标是拒绝原假设,它的核心是证伪。一般来说我们在多个备选项中选出其中的某一个有两种思考过程,一种是基于满意法的思考,也就是找到那个看上去最可信的假设;另一种是证伪法,即剔除掉那些无法被证实的假设。
满意法的严重问题是,当人们在没有对其他假设进行透彻分析的情况下就坚持其中一个假设,当反面证据如山时往往也视而不见。而证伪法能克服人们专注于某一个答案而忽视其他答案,减少犯错误的可能性。
在A/B Test中,我们不是要估算全部用户的转化率,而是选出实验组和对照组中的的更优方案。因此A/B Test的估计量不再是转化率P,而$P_2-P_1$(实验组和对照组的转化率之差)。原假设是$P_2-P_1=0$(即两者没差别),因为只有当你怀疑实验组和对照组不一样,你才有做实验的动机,所以我们支持的备择假设是$P_2-P_1\neq0$(两者有差别)。如果$P_2-P_1\neq0$,我们还需要确定这种差异是否具有统计上的显著性以支撑我们全量上线实验组方案。
由于抽样误差的存在,A/B Test可能出现以下四种结果,其中当原假设H0为真,却拒绝原假设和当H0为假,却没有拒绝H0是假设检验的两类错误,分别用$\alpha$和$\beta$表示,相应的,做出正确判断的概率分别是$1-\alpha$和$1-\beta$。
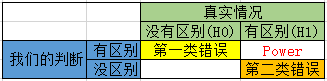
- 第一类错误(Type I error):实际没有区别,我们的判断是有区别。我们把第一类错误出现的概率用$\alpha$表示。这个$\alpha$,就是Significance Level。
- 第二类错误(Type II error):实际有区别,我们的判断是没有区别。用$\beta$表示。根据条件概率的定义,可以计算出$\beta=1-power$。
对于一段的实验:
- 第一类错误$\alpha$不超过5%。也就是说,Significance Level=5%。
- 第二类错误$\beta$不超过20%。也就是说,Statistical Power=1-$\beta$=80%。
犯第一类错误的概率$\alpha$与犯第二类错误的概率$\beta$之间的关系如下图:
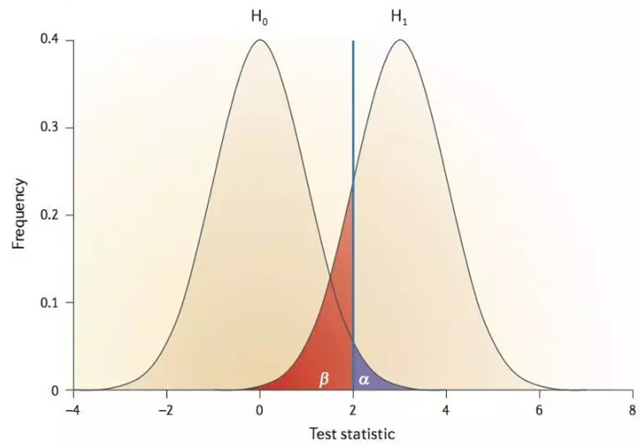
问题:为什么第一类错误比较严格,而第二类错误相对来说比较宽松($\alpha$是5%,$\beta$是20%)?从业务角度可以理解为宁可放弃四个好的产品也不能让一个不好的产品上线。
样本量计算
实验所需样本量的一般公式
统计学里有最小样本量计算公式如下:
$$n=\frac{\sigma^2}{\Delta^2}(Z_{\frac{\alpha}{2}}+Z_{\beta})^2$$
其中:
- n是每组所需样本量,因为A/B测试一般至少2组,所以实验所需样本量为2n
- $\alpha$和$beta$分别称为第一类错误概率和第二类错误概率,一般分别取05和0.2
- Z为正态分布的分位数函数
- $\Delta$为两组数值的差异,如点击率1%到5%,那么$\Delta$就是0.5%
- $\sigma$为标准差,是数值波动性的衡量,$\sigma$越大表示数值波动越厉害。
从这个公式可以知道,在其他条件不变的情况下,如果实验两组数值差异越大或者数值的波动性越小,所需要的样本量就越小。
比例类数值所需样本量的计算实际A/B测试中,我们关注的较多的一类是比例类的数值,如点击率、转化率等。这类比例类数值的特点是,对于某一个用户(样本中的每一个样本点)其结果只有两种,“成功”或“未成功”;对于整体来说,其数值为结果是“成功”的用户数所占比例。如转化率,对于某个用户只有成功转化或未成功转化。比例类数值的假设检验在统计学中叫做两样本比例假设检验。其最小样本量计算的公式为:
$$n=\frac{(Z_{\frac{\alpha}{2}}\cdot\sqrt{2\cdot\frac{(p_1+p_2)}{2}\cdot(1-\frac{(p_1+p_2)}{2})}+Z_{\beta}\cdot\sqrt{p_1\cdot(1-p_1)+p_2\cdot(1-p_2)})^2}{|p_1-p_2|^2}$$
上面式子中$p_1$我们称为基础值,是实验关注的关键指标现在的数值(对照组);$p_2$我们称为目标值,是希望通过实验将其改善至的水平。
样本量计算的实现
除了使用线上工具外,样本量的计算也可以通过程序来实现。
Python实现:
from statsmodels.stats.power import zt_ind_solve_power from statsmodels.stats.proportion import proportion_effectsize as es zt_ind_solve_power(effect_size=es(prop1=0.30, prop2=0.305), alpha=0.05, power=0.8, alternative="two-sided")
参考链接:



