比t-SNE更好的降维算法UMAP

!文章内容如有错误或排版问题，请提交反馈，非常感谢！

针对高维数据的降维，先前使用的是t-SNE。无意中接触到UMAP，发现还是蛮有啥意思的。整理了一些资料供以后深入研究。

UMAP简介

UMAP，全称 uniform manifold approximation and projection，统一流形逼近与投影，是基于黎曼几何和代数拓扑的理论框架结构构建的。在处理大数据集时，UMAP优势明显，运行速度更快，内存占用小。UMAP是一种降维技术，类似于t-SNE，可用于可视化，但也可用于一般的非线性降维。该算法基于关于数据的三个假设：

数据均匀分布在黎曼流形上（Riemannian manifold）
黎曼度量是局部恒定的（或可以这样近似）
流形是局部连接的

根据这些假设，可以对具有模糊拓扑结构的流形进行建模。通过搜索具有最接近的等效模糊拓扑结构的数据的低维投影来找到嵌入。

相对于t-SNE，其主要特点：降维快准狠。

UMAP vs. t-SNE

特性	UMAP	t-SNE
计算速度	更快（优化算法）	较慢（复杂度高）
全局结构保留	更好	较差（侧重局部）
参数敏感性	对 n_neighbors 敏感	对困惑度（perplexity）敏感
大数据集支持	支持百万级数据	通常限于万级数据
数学基础	基于流形和拓扑理论	基于概率分布匹配

优缺点

优点：

高效处理大规模数据。
同时保留局部和全局结构。
支持自定义距离度量，灵活性高。

缺点：

参数调整影响显著（需根据数据调整 n_neighbors 和 min_dist）。
理论复杂性较高，实现细节对结果敏感。

应用场景

数据可视化：单细胞RNA测序（scRNA-seq）、图像嵌入、文本数据等。
预处理：为分类、聚类任务提取低维特征。
异常检测：在低维空间更容易识别离群点。

论文：McInnes, L, Healy, J, UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, arXiv e-prints 1802.03426, 2018

UMAP的原理

核心思想

UMAP基于以下两个关键理论：

流形假设：高维数据分布在一个低维流形上。
拓扑分析：通过构建高维和低维空间的模糊拓扑结构（fuzzy simplicial sets），并最小化两者之间的差异。

其目标是通过保持高维数据中的局部邻域关系和全局结构，将数据映射到低维空间（如2D或3D）。

算法步骤

构建高维图（High-Dimensional Graph）

邻域定义：对每个数据点，基于距离（如欧氏距离）确定其`n_neighbors`个最近邻。
概率计算：为每个点与其邻居构建一个模糊的邻域关系（通过概率权重），使用以下公式：

$$p_{j|i}=\exp(-\frac{d(x_i,x_j)-\rho_i}{\sigma_i})$$

$\rho_i$：点$x_i$到其最近邻的距离（保证局部连通性）。
$\sigma_i$：通过二分搜索确定，确保每个点的邻域权重之和为固定值。

构建低维图（Low-Dimensional Graph）

在低维空间（如2D）随机初始化点。
定义低维空间的概率分布（使用学生t分布）：

$$q_{ij}=\left(1+a \cdot d(y_i,y_j)^{2b}\right)^{-1}$$

$a,b$：超参数，通常固定为93和0.79，以近似高维空间的关系。

优化损失函数

最小化高维和低维分布之间的交叉熵损失：

$$\text{Loss}=\sum_{i,j}p_{ij}\log(\frac{p_{ij}}{q_{ij}})+(1-p_{ij})\log(\frac{1-p_{ij}}{1-q_{ij}})$$

通过梯度下降（如随机梯度下降）优化低维坐标。

关键超参数

n_neighbors：控制局部与全局结构的平衡。值越小，保留更多局部结构；值越大，保留更多全局结构（默认15）。
min_dist：低维空间中点之间的最小距离，影响聚类紧密程度（默认1）。
metric：距离度量方式（如欧氏距离、余弦距离等）。
n_components：降维后的维度（通常为2或3）。

UMAP的使用

安装：pip install umap-learn

umap包继承了sklearn类，因此与其他具有相同调用API的sklearn转换器紧密地放在一起。UMAP主要参数

n_neighbors：这决定了流形结构局部逼近中相邻点的个数。更大的值将导致更多的全局结构被保留，而失去了详细的局部结构。一般来说，这个参数应该在5到50之间，10到15是一个合理的默认值。
min_dist: 这控制了嵌入的紧密程度，允许压缩点在一起。数值越大，嵌入点分布越均匀;数值越小，算法对局部结构的优化越精确。合理的值在001到0.5之间，0.1是合理的默认值。
n_components：作为许多scikit学习降维算法的标准，UMAP提供了一个n_components参数选项，允许用户确定将数据嵌入的降维空间的维数。与其他一些可视化算法（如t-SNE）不同，UMAP在嵌入维度上具有很好的伸缩性，因此您可以使用它进行二维或三维的可视化。
metric: 这决定了在输入空间中用来测量距离的度量的选择。已经编写了各种各样的度量标准，用户定义的函数只要经过numba的JITd处理就可以传递。

以sklearn内置的Digits Data这个数字手写识别数据库为例。

from sklearn.datasets import load_digits
import matplotlib.pyplot as plt

digits = load_digits()
fig, ax_array = plt.subplots(20, 20)
axes = ax_array.flatten()
for i, ax in enumerate(axes):
    ax.imshow(digits.images[i], cmap='gray_r')
plt.setp(axes, xticks=[], yticks=[], frame_on=False)
plt.tight_layout(h_pad=0.5, w_pad=0.01)
plt.show()

DigitsData每个数字是64维的向量，先查看数据：

使用umap降至2维并绘制散点图：

from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
import umap
import numpy as np

digits = load_digits()

reducer = umap.UMAP(random_state=42)
embedding = reducer.fit_transform(digits.data)
print(embedding.shape)

plt.scatter(embedding[:, 0], embedding[:, 1], c=digits.target, cmap='Spectral', s=5)
plt.gca().set_aspect('equal', 'datalim')
plt.colorbar(boundaries=np.arange(11)-0.5).set_ticks(np.arange(10))
plt.title('UMAP projection of the Digits dataset')
plt.show()

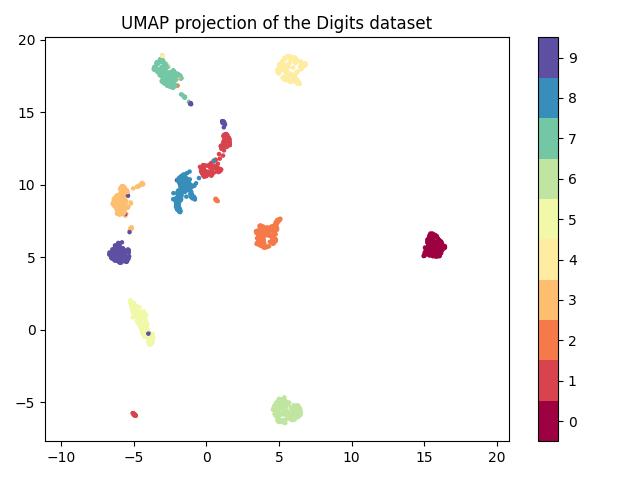
从图上可以看出，相同的数字大多聚在一起了。

参考链接：

比t-SNE更好的降维算法UMAP

UMAP简介

UMAP的原理

核心思想