使用scipy.optimize寻找函数最优解

scipy.optimize简介

scipy.optimize 是 Python 中 SciPy 库的一个模块，专门用于数学优化。这个模块包含了一系列的函数和算法，用于求解最小化（或最大化）问题、方程组的根、以及执行曲线拟合。这些功能对于科学计算、工程设计、数据分析等领域非常重要。以下是 scipy.optimize 的几个关键特性和常用函数：

minimize：用于求解最小化问题。它支持多种算法（如 BFGS、Nelder-Mead、Newton-Conjugate-Gradient 等），适用于有约束和无约束的优化。
root：用于寻找非线性方程组的根。支持多种算法，如 ‘hybr’、’lm’、’broyden1’ 等。
curve_fit：用于数据拟合。它基于最小二乘法，可以估计模型参数。
linprog：用于解决线性规划问题，即在一系列线性约束下最小化线性目标函数。
differential_evolution：用于求解全局优化问题，适用于复杂的、可能具有多个局部最小值的问题。

其中最常用的是scipy.optimize.minimize。

scipy.optimize.minimize简介

scipy.optimize.minimize 是 SciPy 库中用于函数最小化的一个主要工具。它提供了一个通用接口，用于在给定一些约束条件的情况下，寻找多变量函数的局部最小值。这个函数非常强大，可以应对各种不同类型的优化问题。

多变量支持：可以处理多个自变量的函数。
多种优化算法：支持多种算法，包括但不限于 Nelder-Mead, Powell, CG, BFGS, Newton-CG, L-BFGS-B, TNC, COBYLA, SLSQP, trust-constr 等。
有约束和无约束优化：可以处理无约束问题，也支持各种约束，包括等式约束和不等式约束。
灵活性：用户可以指定优化算法，设置各种选项（如迭代次数上限、容忍度等）。

函数格式：

scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)

参数含义：

参数	类型	含义
fun	callable	要最小化的目标函数。fun(x, *args) -> float 其中 $x$ 是一个带有形状($n$)的一维数组，$args$ 是完全指定函数所需的固定参数的元组。
x0	ndarray, shape (n,)	初始猜测: 大小为($n$)的实元素的数组，其中 $n$ 是变量的数目。
args	tuple, optional	额外的参数传递给目标函数及其导数(fun、 jac 和 hess 函数)。
method	str or callable, optional	求解器的类型，如果没有给出，则根据问题是否有约束或边界，选择 BFGS、 L-BFGS-B、 SLSQP 中的一个。
jac	{callable, ‘2-point’, ‘3-point’, ‘cs’, bool}, optional	梯度向量的计算方法。只适用于 CG，BFGS，Newton-CG，L-BFGS-B，TNC，SLSQP，dogleg，trust-ncg，trust-krylov，trust-fine 和 trust-Constr。如果它是可调用的，那么它应该是一个返回梯度向量的函数
hess	{callable, ‘2-point’, ‘3-point’, ‘cs’, HessianUpdateStrategy}, optional	计算 Hessian 矩阵的一种方法。只适用于 Newton-CG，dogleg，trust-ncg，trust-krylov，trust-fine 和 trust-constr. 。如果它是可调用的，它应该返回黑森矩阵
hessp	callable, optional	目标函数的 Hessian 乘以任意向量 p。只适用于 Newton-CG，trust-ncg，trust-krylov，trust-Constr。只需要一个 Hessp 或者 Hess 就够了。如果提供 hess，那么 hessp 将被忽略。Hessp 必须计算 Hessian 乘以任意向量。
bounds	sequence or Bounds, optional	Nelder-Mead，L-BFGS-B，TNC，SLSQP，Powell 和 trust-conr 方法的变量界。
constraints	{Constraint, dict} or List of {Constraint, dict}, optional	约束条件。仅适用于 COBYLA、 SLSQP 和 trust-Constr。
tol	float, optional	终止公差。指定 tol 后，所选的最小化算法会将一些相关的特定于求解器的公差设置为 tol。要进行详细控制，请使用特定于求解器的选项。
options	dict, optional	求解器选项字典。除 TNC 外的所有方法都接受以下通用选项:maxiter int：要执行的最大迭代次数。根据方法，每次迭代可能使用多个函数评估。disp bool：设置为 True 可打印消息。
callback	callable, optional	在每次迭代之后调用。对于“trust-conr”，它是一个带有签名的可调用函数
res	Optimize Result	优化结果表示为 OptimizeResult 对象。重要的属性有：x 解决方案数组success 一个布尔标志，指示优化器是否成功退出，以及描述终止原因的消息。有关其他属性的说明，请参阅 OptimizeResult。

method 支持的算法：

求解器	中文名	jac要求	hess要求	边界约束	条件约束	求解规模
Nelder-Mead	单纯形法	无	无	可选	无	小
Powell	鲍威尔法	无	无	可选	无	小
CG	共轭梯度法	可选	无	无	无	中小
BFGS	拟牛顿法	可选	无	无	无	中大
Newton-CG	牛顿共轭梯度法	必须	可选	无	无	大
L-BFGS-B	限制内存BFGS法	可选	无	可选	无	中大
TNC	截断牛顿法	可选	无	可选	无	中大
COBYLA	线性近似法	无	无	无	可选	中大
SLSQP	序列最小二乘法	可选	无	可选	可选	中大
trust-constr	信赖域算法	无	可选	可选	可选	中大
dogleg	信赖域狗腿法	必须	可选	无	无	中大
trust-ncg	牛顿共轭梯度信赖域法	必须	可选	无	无	大
trust-krylov	子空间迭代信赖域法	必须	可选	无	无	大
trust-exact	高精度信赖域法	必须	可选	无	无	大

optimize.minimize算法介绍

单纯形法Nelder-Mead

Nelder-Mead 单纯形法是一种用于函数优化的数学算法，特别适用于没有导数的优化问题。这种方法由 John Nelder 和 Roger Mead 在 1965 年提出，是一种启发式搜索算法，用于寻找多变量函数的最小值。

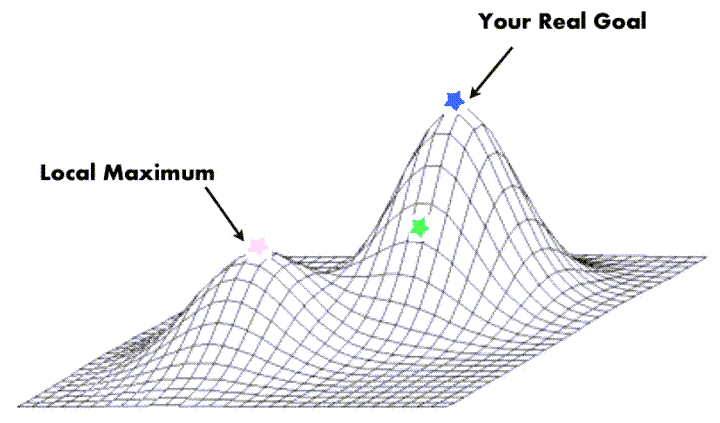
基本概念

单纯形（Simplex）：在 Nelder-Mead 方法中，单纯形是算法的核心概念。在 N 维空间中，一个单纯形由 N+1 个顶点组成，这些顶点定义了一个几何形状。例如，在二维空间中，单纯形是一个三角形；在三维空间中，它是一个四面体。
启发式搜索：该方法不依赖于函数的梯度或导数，而是通过比较单纯形顶点处的函数值来搜索最小值。这使得它特别适用于那些导数难以计算或不存在的函数。

工作原理

Nelder-Mead 算法主要通过以下步骤对单纯形进行迭代和调整，以逼近最小值：

初始化：选择 N+1 个初始点来形成一个初始单纯形。
评估：在单纯形的每个顶点处计算目标函数的值。
变换：根据顶点的函数值执行一系列变换（反射、扩张、收缩、缩减），以改变单纯形的形状和位置。这些变换旨在将单纯形移向函数值较低的区域。
- 反射：尝试通过反射单纯形中最差点到其它点构成的超平面的另一侧来改善最差点。
- 扩张：如果反射成功，进一步尝试沿同一方向扩大步伐。
- 收缩：如果反射未成功，尝试通过缩小步伐在更小的范围内搜索。
- 缩减：如果其他方法都失败了，缩减整个单纯形，除了最优点之外的所有点都朝最优点移动。
迭代：重复上述步骤，直到满足停止准则（例如，单纯形的大小小于预定阈值，或者函数值的改善不再显著）。

优点

适用性广：适用于不可导或导数难以计算的函数。
简单易用：算法概念简单，容易实现。

缺点

效率问题：对于高维问题或特别复杂的函数，该方法可能效率低下。
不保证收敛：在某些情况下，Nelder-Mead 算法可能不会收敛到全局最小值。
缺乏理论保证：与基于梯度的优化方法相比，它缺乏严格的理论收敛保证。

适用场景

Nelder-Mead方法，也称为单纯形法，是一种用于非线性优化问题的数值方法。这种方法特别适用于以下几种场景：

导数无法获取或不准确：当优化问题的目标函数复杂，难以计算导数，或者导数不准确时，Nelder-Mead方法非常有用。这包括一些基于实验数据或经验公式的模型。
低维问题：Nelder-Mead方法通常用于低维（通常是少于10维）的优化问题。在高维问题中，该方法的效率和效果可能会降低。
非平滑或不连续的目标函数：对于那些不连续或非光滑的目标函数，传统的基于梯度的优化方法可能不适用，而Nelder-Mead方法可以提供更好的结果。
全局探索：尽管Nelder-Mead方法不能保证找到全局最优解，但它在搜索全局最优解时表现出一定的鲁棒性，尤其是在搜索空间不大的情况下。
实验设计和统计建模：在实验设计和统计建模中，当模型复杂且含有多个变量时，Nelder-Mead方法可以用来寻找最优解或进行模型调整。
计算资源受限：由于Nelder-Mead方法不需要计算导数，它在计算资源有限的环境中（如小型嵌入式系统）可以作为一种有效的优化手段。
初步优化探索：在对问题的理解不够深入时，Nelder-Mead方法可以用作初步探索工具，帮助确定更复杂算法的合适起始点。

注意事项

Nelder-Mead方法可能会在非凸问题上陷入局部最小值。
在高维问题中，该方法的效率和准确性可能不足。
相比于其他优化算法，Nelder-Mead方法在寻找精确最优解方面可能不够精确。

总体而言，Nelder-Mead单纯形法是一种简单且易于实现的优化方法，适用于那些对导数要求不高的非线性优化问题。

鲍威尔法Powell

鲍威尔法（Powell’s Method）是一种用于寻找多变量函数最小值的优化算法。这种方法由Michael J.D. Powell在1964年提出，它是一种无导数优化算法，适用于那些不需要函数导数的情况，尤其是当导数难以计算或不存在时。

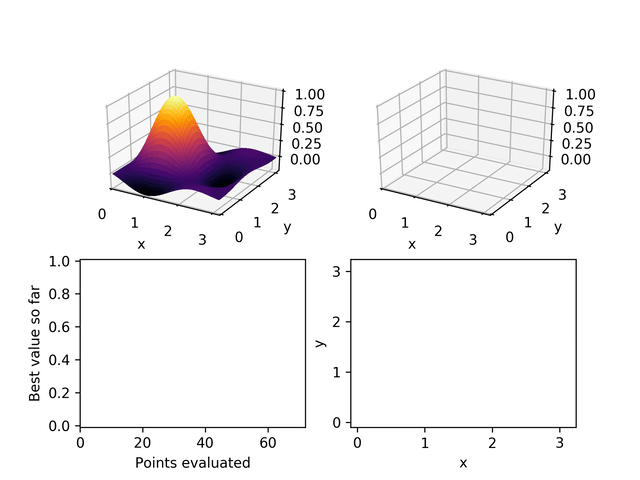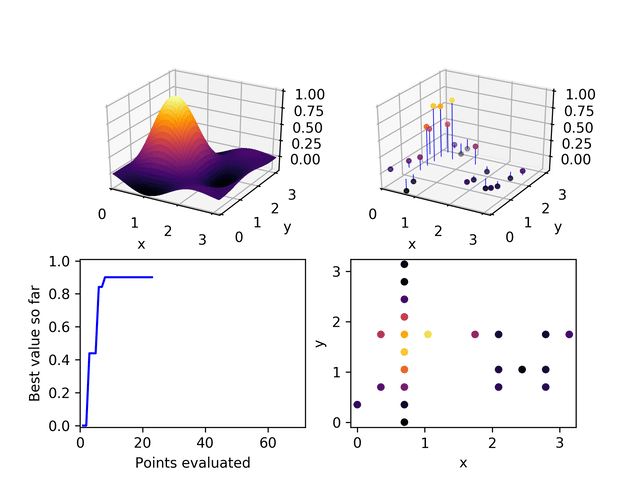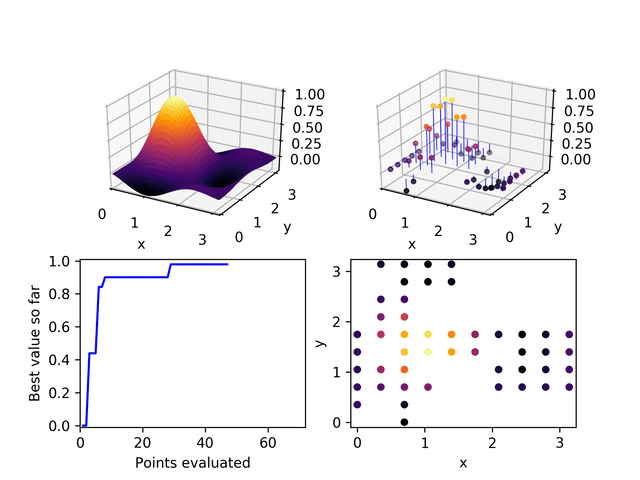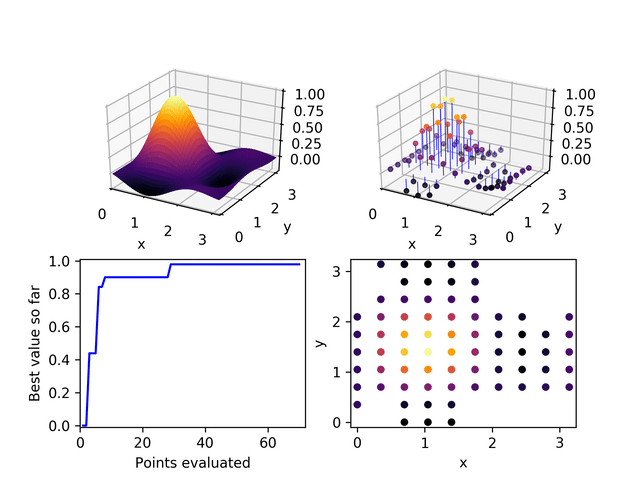
基本概念

方向集合：鲍威尔法在每一步迭代中使用一组方向，这些方向不必是正交或规范的。
线搜索：算法沿着选定的方向进行搜索，以找到函数值降低的点。

工作原理

鲍威尔法主要通过以下步骤进行：

初始化：选择一个起始点和一组初始方向，通常是坐标轴方向。
线搜索：对每个方向进行线搜索，以找到该方向上的最小值点。
更新方向：更新方向集合，通常是替换其中一个方向为指向最新找到的最小值点的方向。
迭代：重复进行线搜索和更新方向，直到满足停止条件（如迭代次数、改进程度等）。

优点

无需导数：不需要计算函数的梯度或海森矩阵（Hessian），适用于不可微函数。
适用性广：可以处理非线性、非凸和无约束的优化问题。

缺点

收敛速度：相比于需要导数的方法，收敛速度可能较慢。
方向依赖性：结果可能依赖于初始方向的选择。
局部最小值：可能只能找到局部最小值，而非全局最小值。

适用场景

鲍威尔法（Powell’s Method）是一种优化算法，主要用于寻找多变量函数的最小值。由于它是一种无导数（derivative-free）方法，因此它特别适用于以下场景：

导数不可用或难以计算：当目标函数复杂，导数难以计算或不存在时，鲍威尔法非常有用。这包括一些实验数据模型和经验公式。
非平滑函数：对于那些不连续或不光滑的函数，传统的基于梯度的优化方法可能不适用。鲍威尔法可以在这些情况下提供更好的结果。
高维问题：虽然在高维空间中效率可能降低，但鲍威尔法仍然可以应用于多变量的优化问题。
初步探索性优化：在对问题了解不深或者当优化问题的结构不清楚时，鲍威尔法可以作为一种探索性工具使用，帮助确定更复杂算法的合适起始点。
工程和科学应用：在工程优化、物理学模型优化、经济学模型等领域，鲍威尔法可以用来优化复杂的模型，尤其是在精确的数学模型难以建立的情况下。
计算资源受限：对于计算资源有限的环境，鲍威尔法由于不需要计算复杂的导数，可以作为一种较为节省资源的优化方法。
实验设计和统计建模：在实验设计中，当模型复杂且含有多个变量时，鲍威尔法可以用来寻找最优解或对模型进行调整。

总的来说，鲍威尔法适用于各种需要优化但又不适合使用基于梯度的方法的场景，尤其是在目标函数复杂或者梯度信息不可用的情况下。然而，需要注意的是，鲍威尔法可能只能保证找到局部最小值，并且在高维问题上可能效率不高。

共轭梯度法CG

共轭梯度法（Conjugate Gradient Method，简称 CG）是一种用于求解特定类型线性方程组的迭代方法，尤其是对于大型稀疏对称正定矩阵。此外，它也被广泛用于非线性优化问题。共轭梯度法由 Hestenes 和 Stiefel 在 1952 年提出。

基本概念

共轭方向：在共轭梯度法中，”共轭”指的是一组特殊的方向，这些方向相对于给定矩阵具有正交性质。在这些方向上进行搜索可以更高效地逼近最优解。
线性方程组：最初，共轭梯度法被设计用来求解形式为 $ Ax = b $的线性方程组，其中$A$是一个大型稀疏对称正定矩阵。

工作原理（线性方程组）

初始化：选择一个初始猜测解$x_0$，计算初始残差$r_0 = b – Ax_0$和初始搜索方向$p_0 = r_0$。
迭代：在每次迭代中，算法更新解$ x$，残差 $ r $和搜索方向 $ p$。更新包括沿当前搜索方向$ p_k $找到一个点，使得在该方向上$ Ax = b$最接近成立。
收敛判断：当残差足够小或达到预设的迭代次数时，算法停止。

扩展到非线性优化

在非线性优化中，共轭梯度法被用于最小化无约束问题的非线性函数。它利用梯度（或近似梯度）信息来生成一系列共轭方向，并在这些方向上进行线搜索。

梯度计算：计算当前点的梯度。
生成共轭方向：使用梯度信息和前一步的方向来生成新的共轭方向。
线搜索：在新的共轭方向上进行线搜索以找到函数的局部最小值。
迭代更新：更新当前点和梯度，然后重复步骤 2 和 3。

优点

效率高：对于大型问题，尤其是稀疏矩阵，比直接方法更有效。
无需存储矩阵：不需要存储整个矩阵，适合处理大规模问题。
适用性广：可以用于广泛的优化问题，特别是对于大型非线性问题。

缺点

对称正定矩阵限制：在线性方程组中，要求矩阵是对称正定的。
可能需要精确的线搜索：在非线性优化中，线搜索步骤可能需要较高的精度。
对初始猜测敏感：结果可能依赖于初始猜测。

适用场景

共轭梯度法（Conjugate Gradient Method）是一种高效的迭代算法，适用于多种类型的优化问题，特别是在处理大型、稀疏的线性系统和某些非线性优化问题时表现出色。以下是共轭梯度法的一些主要适用场景：

大型稀疏线性系统：当求解大型的稀疏对称正定线性方程组（如 $Ax = b$）时，共轭梯度法特别有效。这种情况常见于科学计算和工程领域，如有限元分析。
大规模优化问题：在处理大规模的非线性优化问题时，共轭梯度法是一种有效的选择，特别是当问题的规模或存储限制使得使用直接方法或基于矩阵分解的方法不切实际时。
机器学习和深度学习：在机器学习和深度学习中，共轭梯度法可以用于大规模的参数优化问题，尤其是在训练具有大量参数的模型时。
图像处理和计算机视觉：在图像处理和计算机视觉领域，共轭梯度法可用于解决大型优化问题，如图像重建和3D建模。
有限资源环境：由于共轭梯度法不需要存储整个矩阵，它适合在内存资源有限的环境中使用，如嵌入式系统或移动设备。
能量最小化和物理建模：在物理学中，共轭梯度法常用于能量最小化问题，例如在分子动力学和量子化学计算中。

注意事项

共轭梯度法对于非对称或非正定矩阵可能不适用。
在非线性优化问题中，算法的表现可能依赖于精确的线搜索。
初始猜测的选择可能影响算法的收敛速度和稳定性。

总体而言，共轭梯度法是处理大型线性和非线性问题的一种高效且存储友好的方法，尤其在需要避免直接矩阵操作的场合中表现出色。

拟牛顿法BFGS

拟牛顿法中的BFGS算法（命名来源于其发明者Broyden, Fletcher, Goldfarb, 和 Shanno）是一种在无约束优化问题中广泛使用的迭代方法。BFGS方法属于拟牛顿法的一种，用于近似牛顿法中的海森矩阵（Hessian matrix），进而寻找多变量函数的极小值点。这种方法在求解中等规模的优化问题时特别有效。

基本原理

海森矩阵：在牛顿法中，使用海森矩阵（函数的二阶导数矩阵）来寻找函数的极小值。但直接计算和存储海森矩阵在大多数实际问题中是不可行的。
近似海森矩阵：BFGS方法不直接计算海森矩阵，而是迭代地更新一个近似的海森矩阵的逆。这种更新依赖于梯度（一阶导数）的信息，从而避免了直接计算二阶导数。

特点

自适应：BFGS方法通过迭代更新来自适应目标函数的特性，无需手动调整。
无需二阶导数：仅依赖于梯度信息，适合于那些海森矩阵难以计算的问题。
效率较高：对于中等规模的问题，BFGS通常比梯度下降法更快收敛。

适用场景

BFGS方法适用于多种无约束优化问题，特别是当目标函数是光滑且连续的。它被广泛应用于：

机器学习模型的参数优化。
经济学和金融中的最优化问题。
工程设计中的优化问题。
科学计算中的能量最小化问题。

限制内存BFGS法 L-BFGS-B

限制内存BFGS法（Limited-memory Broyden-Fletcher-Goldfarb-Shanno，简称L-BFGS-B）是一种在大规模优化问题中广泛使用的算法，尤其适合于具有边界约束的情况。这种算法是标准BFGS算法的变种，旨在减少在大规模问题中存储和计算近似海森矩阵所需的内存。

基本原理

L-BFGS-B算法基于BFGS方法，它使用了一种特殊的策略来存储近似海森矩阵的有限数量的更新，从而减少内存使用。这种方法使得算法能够有效地处理有成千上万个变量的优化问题。

特点

内存效率：适合处理大规模优化问题，因为它不需要存储完整的近似海森矩阵。
边界约束处理：可以有效地处理有边界约束的问题。
适用性广：适用于大多数光滑目标函数。

适用场景

大规模问题：特别适用于变量数量庞大的优化问题。
带边界约束的问题：能够处理变量受到上下界限制的情况。
机器学习和深度学习：在这些领域中，经常需要优化大量的参数。
科学计算和工程设计：在需要处理边界约束的复杂优化问题中。

总结来说，L-BFGS-B是一个适用于大规模、带有边界约束优化问题的高效算法，特别适合于需要处理大量变量的情况。

牛顿共轭梯度法 Newton-CG

牛顿共轭梯度法（Newton-Conjugate Gradient，简称Newton-CG）是一种用于求解无约束优化问题的高效算法，它结合了牛顿法和共轭梯度法的优点。该方法特别适合于求解大规模的优化问题，尤其是当直接计算或存储海森矩阵（Hessian matrix，即目标函数的二阶导数矩阵）不切实际时。

基本原理

牛顿法依赖于目标函数的一阶和二阶导数（即梯度和海森矩阵）。在每一步迭代中，牛顿法通过求解线性方程组$H_k \Delta x = -\nabla f(x_k)$来更新解，其中$H_k$是海森矩阵，$\nabla f(x_k)$是梯度。然而，对于大规模问题，直接计算和存储 $H_k$可能非常困难。

牛顿共轭梯度法解决了这个问题。它不是直接计算$H_k$，而是使用共轭梯度法来近似求解上述线性方程组。这样，只需计算海森矩阵与向量的乘积，而无需直接构造和存储整个海森矩阵。

特点

高效性：对于大规模问题，牛顿共轭梯度法比传统牛顿法更加高效，因为它不需要直接计算和存储海森矩阵。
精确性：由于使用了二阶导数信息，该方法通常比只使用一阶导数的方法更精确。
灵活性：适用于大多数无约束优化问题，特别是目标函数光滑且连续的情况。

适用场景

大规模优化问题：当问题规模较大，直接计算和存储海森矩阵不切实际时。
机器学习参数优化：在机器学习中，尤其是对于具有大量参数的模型。
科学计算和工程优化：适用于需要精确解的复杂问题。

总结来说，牛顿共轭梯度法是一种结合了牛顿法精确性和共轭梯度法高效性的优化算法，特别适合于大规模的无约束优化问题。

截断牛顿法TNC

截断牛顿法（Truncated Newton Method，简称TNC）是一种用于求解大规模优化问题的算法，特别是在问题具有大量变量且需要精确解时。它是牛顿法的一个变体，通过在每次迭代中使用迭代求解器（例如共轭梯度法）来近似求解牛顿方程，从而减少计算成本。

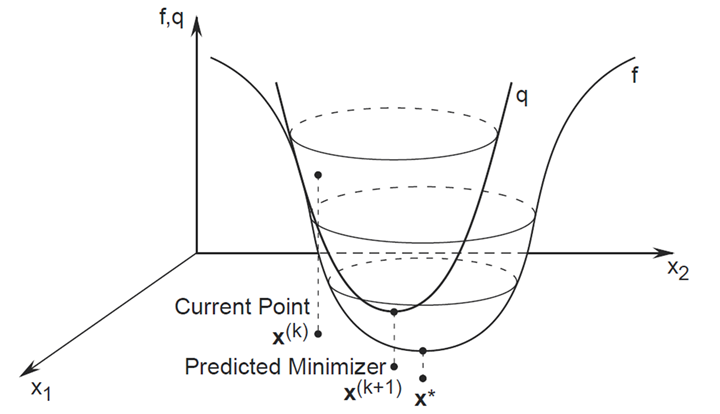
基本原理

截断牛顿法基于牛顿法的基本思想，牛顿法利用二阶泰勒展开来近似目标函数，并通过求解牛顿方程 ( H_k \Delta x = -\nabla f(x_k) ) 来更新解，其中 ( H_k ) 是海森矩阵，( \nabla f(x_k) ) 是梯度。然而，在大规模问题中，直接求解这个方程组可能非常耗时。

为了解决这个问题，截断牛顿法在每次迭代中使用一个迭代求解器（如共轭梯度法）来近似求解牛顿方程。这种方法不需要完整的海森矩阵，只需要能够计算海森矩阵与向量的乘积。因此，它特别适用于那些海森矩阵难以存储或计算的大规模问题。

特点

高效性：对于大规模问题，截断牛顿法可以在不牺牲太多精度的情况下显著减少计算成本。
适用性广：适用于大多数无约束或有约束的优化问题。
灵活性：可以根据问题的特点选择不同的迭代求解器。

适用场景

大规模优化问题：尤其是那些变量数量巨大，计算和存储完整海森矩阵不切实际的问题。
机器学习和深度学习：在训练具有大量参数的模型时。
科学计算和工程设计：适用于需要精确解的复杂问题。

总结来说，截断牛顿法是一种高效的优化算法，适用于大规模的无约束或有约束优化问题，特别是在海森矩阵难以直接计算或存储的情况下。

线性近似法COBYLA

线性近似法（Constrained Optimization BY Linear Approximations，简称COBYLA）是一种用于求解无约束或有约束的优化问题的数值优化方法。它属于无导数优化算法，特别适用于目标函数或约束条件的导数信息难以获得或不存在的情况。

基本原理

COBYLA算法通过构建目标函数和约束条件的线性近似来寻找最优解。这种方法不依赖于梯度信息，因此适用于不可微或导数难以计算的函数。算法主要通过迭代更新一组线性模型，用于近似表示目标函数和约束条件。

特点

无需导数信息：适用于那些目标函数或约束条件不可微或导数难以获得的问题。
灵活性：能够处理无约束和有约束的优化问题。
适用性广泛：适用于多种类型的优化问题，包括线性和非线性问题。

适用场景

无导数优化：当目标函数的梯度信息不可用或难以计算时。
有约束优化问题：特别是当约束条件复杂或难以精确表达时。
工程设计和科学计算：在需要进行参数优化但导数信息不可用的情况下。

总结来说，COBYLA是一种灵活且广泛适用的优化算法，特别适合于那些目标函数或约束条件的导数信息难以获取的情况。

序列最小二乘法 SLSQP

序列最小二乘法（Sequential Least SQuares Programming，简称SLSQP）是一种用于求解非线性优化问题的算法，特别是在目标函数和约束条件都是非线性时。它结合了最小二乘法和二次规划的特点，在迭代过程中逐步求解一系列二次规划（QP）子问题，从而逼近最终的最优解。

基本原理

SLSQP算法的基本思想是将原始的优化问题分解成一系列小规模的二次规划问题。每个子问题都是在目标函数的当前近似下，对原问题的局部线性化或二次化。通过求解这些子问题，算法逐步改进对最优解的近似。

特点

适用性广：能够处理线性和非线性的约束条件和目标函数。
效率较高：通过解决一系列二次规划子问题来逐步逼近最优解，通常比直接求解原始非线性问题要高效。
准确性：提供了对原问题较好的近似，特别是当问题可以被合理地局部线性化或二次化时。

适用场景

非线性优化问题：尤其是当问题包含复杂的非线性约束和目标函数时。
工程设计和控制问题：在这些领域中，经常需要考虑多种约束条件。
经济学和运筹学：在资源分配、成本最小化等问题中应用。

总结来说，SLSQP是一种高效、广泛适用的非线性优化算法，它通过序列地解决最小二乘问题，适用于各种含有复杂约束条件的优化问题。

信赖域算法 trust-constr

信赖域算法（Trust-Region Method，也称为trust-constr）是一种用于求解非线性优化问题的算法。它在每一步迭代中构建一个目标函数的局部近似模型，并在一个定义良好的区域（称为“信赖域”）内寻找最优点。这种方法在处理有约束和无约束优化问题时都很有效，特别是当目标函数复杂或梯度难以计算时。

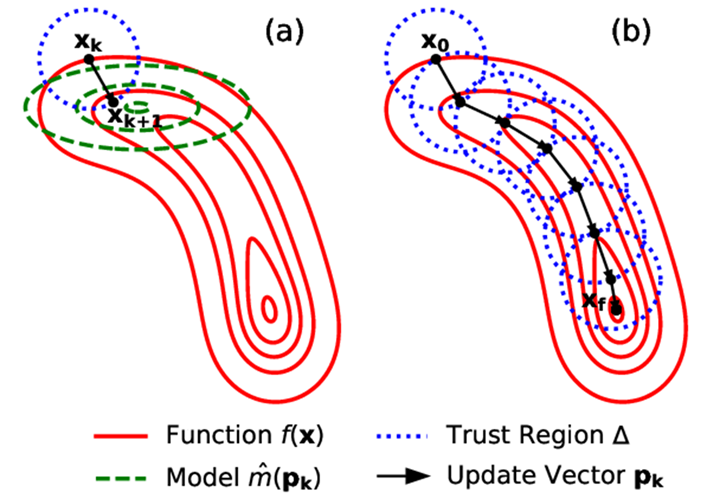
基本原理

信赖域方法的核心思想是在每次迭代中围绕当前点构建一个目标函数的局部模型（通常是二次模型），并在一个预定义的区域（即信赖域）内寻找局部最优解。信赖域的大小反映了对当前局部模型的信任程度：如果局部模型在当前点附近提供了良好的近似，信赖域可以扩大；如果近似效果不好，则缩小信赖域。

特点

适应性强：通过调整信赖域的大小，算法可以适应目标函数的局部特性。
全局和局部收敛性：提供了良好的全局和局部收敛特性，尤其适用于非线性和非凸问题。
适用性广泛：适用于无约束和有约束的优化问题，包括线性和非线性约束。

适用场景

非线性优化问题：特别是当目标函数复杂或不容易求导时。
工程设计和科学计算：在这些领域中，经常需要解决具有复杂约束的优化问题。
机器学习和数据分析：在模型参数优化和特征选择等方面应用。

总结来说，信赖域算法是一种灵活且强大的优化工具，适用于各种类型的非线性优化问题，能够有效处理复杂的约束和不规则的目标函数。

信赖域狗腿法 dogleg

信赖域狗腿法（Dogleg Method）是一种特别的信赖域算法，用于求解非线性最优化问题。这种方法的特点是在每次迭代中，根据目标函数的性质，选择一个特定的路径（称为“狗腿路径”）来更新解。狗腿法特别适用于目标函数是二次的或接近二次的情况。

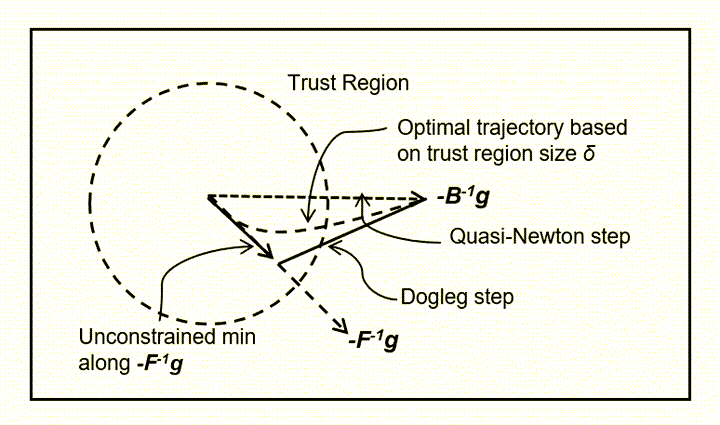
基本原理

狗腿法在信赖域框架下工作，其核心思想是结合了梯度下降法和牛顿法的路径。这个路径分为两段：第一段是沿着梯度方向（类似于梯度下降），第二段则转向牛顿方向。这样的路径形状类似于狗的后腿，因此得名“狗腿法”。

工作流程

初始化：选择一个初始点和信赖域的大小。
迭代过程：
- 在当前信赖域内，根据目标函数的梯度和海森矩阵（或其近似），构建狗腿路径。
- 选择路径上的点作为新的迭代点，这一点既要在信赖域内，又要尽可能减少目标函数的值。
- 根据新点的性能，调整信赖域的大小。
终止条件：当梯度足够小或满足其他停止准则时，算法终止。

特点

效率高：结合了梯度下降法和牛顿法的优点，能够在保证收敛速度的同时减少计算量。
适用性强：适用于目标函数是二次的或近似二次的情况。
适应性：通过调整信赖域的大小，能够适应目标函数的不同特性。

适用场景

非线性最优化问题：特别是当目标函数近似为二次函数时。
工程设计和科学计算：在这些领域中的优化问题往往可以利用狗腿法高效求解。
机器学习中的参数优化：在某些情况下，模型的参数优化可以利用狗腿法来加速收敛。

总结来说，信赖域狗腿法是一种高效且适用性强的非线性优化方法，它通过特定的路径选择在保证收敛速度的同时减少计算量，适用于多种类型的优化问题。

牛顿共轭梯度信赖域法 trust-ncg

牛顿共轭梯度信赖域法（Trust-Region Newton-Conjugate-Gradient Method，简称Trust-NCG）是一种结合了信赖域算法和共轭梯度方法的非线性优化算法。这种方法特别适用于大规模问题，尤其是当目标函数的海森矩阵难以直接计算或存储时。

基本原理

Trust-NCG算法在信赖域框架下工作，它使用牛顿方法来构建每个迭代点的局部近似模型。然而，与传统牛顿方法不同的是，该算法使用共轭梯度法来近似求解牛顿方程$H_k \Delta x = -\nabla f(x_k)$，其中$H_k$是海森矩阵，$\nabla f(x_k)$是梯度。这种方法无需直接计算完整的海森矩阵，适用于大规模问题。

特点

适用于大规模问题：由于不需要显式计算和存储海森矩阵，这使得Trust-NCG特别适用于大规模优化问题。
效率高：共轭梯度法的使用减少了计算量，同时保持了较高的求解精度。
灵活性和稳健性：通过调整信赖域的大小，可以有效应对目标函数的非线性和非凸特性。

适用场景

大规模非线性优化问题：特别是那些海森矩阵难以直接计算或存储的情况。
机器学习和深度学习中的参数优化：在训练大型模型时经常遇到的大规模优化问题。
科学计算和工程设计：需要处理复杂模型的优化问题，其中计算资源可能受限。

总结来说，牛顿共轭梯度信赖域法是一种高效且适用于大规模非线性优化问题的算法，特别是在海森矩阵难以直接处理的情况下。通过结合信赖域框架和共轭梯度法，它在保证计算效率的同时，提供了良好的收敛性和稳健性。

子空间迭代信赖域法 trust-krylov

子空间迭代信赖域法（Trust-Region Subspace Iterative Method，简称Trust-Krylov）是一种高效的非线性优化算法，它结合了信赖域方法的思想和Krylov子空间迭代的技术。这种方法特别适合处理大规模非线性优化问题，尤其是在目标函数的海森矩阵难以直接计算或存储的情况下。

基本原理

Trust-Krylov方法的核心是在每次迭代中，使用Krylov子空间迭代技术来构建目标函数的局部近似模型。这种方法不需要完整地计算或存储海森矩阵，而是通过迭代生成一个较小的子空间，在这个子空间中求解近似的牛顿方程。

特点

高效处理大规模问题：通过使用Krylov子空间迭代，算法能够有效处理大规模问题，尤其是海森矩阵难以直接处理的情况。
减少计算资源需求：不需要显式地计算和存储海森矩阵，从而节省计算资源。
适应性强：通过调整信赖域的大小，算法可以适应目标函数的局部特性，提高优化效率。

适用场景

大规模非线性优化问题：特别适用于处理目标函数或约束条件复杂的大规模问题。
科学计算和工程设计：在这些领域中的优化问题，尤其是那些涉及大量变量和复杂模型的问题。
机器学习和数据分析：在大规模数据集或复杂模型参数优化时非常有效。

总体而言，子空间迭代信赖域法是一种在处理大规模非线性优化问题时非常有效的算法，它结合了信赖域方法的稳健性和Krylov子空间技术的高效性，适用于广泛的应用场景。

高精度信赖域法 trust-exact

高精度信赖域法（Trust-Region Exact Method，简称Trust-Exact）是一种非线性优化算法，它在信赖域方法的基础上，致力于提供更精确的解决方案。这种方法特别强调在每次迭代中尽可能精确地求解局部模型的优化问题，从而在整个优化过程中保持较高的精度。

基本原理

Trust-Exact方法在信赖域框架下工作，它构建了目标函数在当前点附近的二次模型。与其他信赖域方法不同的是，Trust-Exact致力于在每次迭代中精确解决这个二次模型的优化问题，而不是寻求近似解。

特点

高精度：通过精确求解局部模型的优化问题，可以提供更高精度的解决方案。
稳健性：继承了信赖域方法的稳健性，能够有效应对目标函数的非线性和非凸特性。
计算资源密集：由于追求高精度解，因此可能需要更多的计算资源，特别是在复杂问题上。

适用场景

对精度要求高的优化问题：在科学计算、工程设计等领域，某些问题需要非常精确的解决方案。
中小规模问题：由于高精度求解需要较多计算资源，因此更适用于中小规模的优化问题。
敏感问题的决策和控制：在需要高度精确控制和决策的场景下，例如机器人控制或精密工程。

总结来说，高精度信赖域法提供了一种在保证解的精度的同时处理非线性优化问题的方法，尤其适用于对解决方案精度要求较高的应用场景。

optimize.minimize算法总结

在实际应用中，最常用的算法可能是BFGS、L-BFGS-B和SLSQP，因为它们在不同类型的问题中都表现良好。BFGS和L-BFGS-B适用于需要梯度信息的情况，而SLSQP则适合于有约束的优化问题。

选择哪种算法主要取决于目标函数的特性（如是否光滑、是否大规模）、是否需要处理约束条件，以及是否有梯度信息。通常，对于没有梯度信息的问题，可以使用Nelder-Mead方法；而对于大规模的问题，通常选择L-BFGS-B或者TNC。如果问题中含有复杂的约束条件，SLSQP是一个不错的选择。

Python中的其他优化包

Pyomo

Pyomo（Python Optimization Modeling Objects）是一个强大的Python库，用于定义和求解各种类型的数学优化问题。Pyomo提供了一种高层次的建模语言，使得用户可以使用Python的语法来表达优化问题，从而使建模过程更加直观和灵活。以下是Pyomo的一些主要特点：

多样的问题类型支持：Pyomo可以用于线性规划（LP）、非线性规划（NLP）、混合整数线性规划（MILP）、混合整数非线性规划（MINLP）和其他更复杂的优化问题。
灵活的模型定义：用户可以利用Python的强大功能，如循环和条件语句，来定义复杂的模型。这使得模型可以更加动态和可扩展。
与多种求解器兼容：Pyomo可以与多种求解器集成，包括开源求解器（如COIN-OR CBC、GLPK）和商业求解器（如CPLEX、Gurobi、Mosek）。
参数化模型：Pyomo支持创建参数化模型，这意味着用户可以轻松地改变模型参数来执行多种情景分析。
数据管理：Pyomo提供了数据管理功能，使得用户可以方便地从多种数据源（如CSV文件、数据库）导入数据到模型中。
高层次的抽象：Pyomo的抽象级别较高，用户无需关注求解器的具体细节，可以专注于模型的构建。

Pyomo在工业界和学术界都有广泛的应用，常用于能源系统规划、供应链管理、生产调度、金融优化等领域。由于其灵活性和强大的功能，它适用于从简单的线性问题到复杂的非线性和混合整数问题。

CVXPY

CVXPY 是一个用于凸优化问题的 Python 建模工具，它提供了一个简洁而强大的界面，使得用户可以方便地构建和求解凸优化问题。CVXPY 的主要特点是其将优化问题的建模和求解过程简化，同时保持了强大的灵活性和表现力。以下是 CVXPY 的一些核心特征：

易于使用：CVXPY 允许用户使用高级的抽象来定义优化问题，这样用户可以专注于问题的数学本质，而不必担心底层的求解细节。
凸优化专用：专门用于定义和求解凸优化问题，包括线性规划、二次规划、锥规划、半定规划等。
强大的求解器支持：支持多种优化求解器，如 ECOS、SCS、OSQP、CPLEX、Gurobi 等。
表达式重写：CVXPY 能够自动重写和简化复杂的数学表达式，使其符合特定求解器的要求。
自动微分和梯度计算：对于需要梯度信息的求解器，CVXPY 能够自动计算所需的梯度。

CVXPY 的易用性和强大功能使其成为解决凸优化问题的理想工具，尤其适合那些对优化领域不太熟悉但需要解决相关问题的用户。

PuLP

PuLP 是一个用于线性规划（LP）和混合整数线性规划（MILP）问题的 Python 库。它提供了一种简单而直观的方式来构建优化模型，并且可以与多种求解器配合使用来求解这些模型。以下是 PuLP 的一些主要特点：

直观的模型构建：PuLP 允许用户使用 Python 语法定义决策变量、目标函数和约束条件，使得模型构建直观易懂。
支持多种求解器：PuLP 可以与多种免费和商业求解器集成，如 CBC、GLPK、CPLEX、Gurobi 等。
适用于 LP 和 MILP：PuLP 特别适用于线性规划和混合整数线性规划问题，可以处理大规模的优化问题。
模型导出：PuLP 允许用户将优化模型导出为不同格式的文件，如 LP 或 MPS，方便与其他优化软件交互。
结果分析：PuLP 提供了便捷的方法来提取和分析优化结果，如变量的最优值和目标函数值。

应用场景

供应链优化：比如确定最佳的物料采购计划、仓库库存管理等。
生产计划：在制造业中，用于生产调度、设备分配等。
物流规划：如车辆路径规划、配送中心的选址问题。
金融问题：例如资产组合优化、风险管理。

PuLP 的易用性和灵活性使其成为处理线性和混合整数优化问题的受欢迎选择，尤其是在业务和工程应用中。

GEKKO

GEKKO 是一个专为工业优化问题设计的 Python 库。它提供了一个高级别的接口，用于构建和求解线性、非线性、整数和混合整数优化问题。GEKKO 特别适用于动态系统的模拟和优化，包括时间序列的优化问题。以下是 GEKKO 的一些主要特点：

支持多种问题类型：GEKKO 可用于求解线性规划（LP）、非线性规划（NLP）、混合整数规划（MIP）、差分方程和动态系统的优化。
动态优化：GEKKO 特别擅长处理动态系统的优化问题，能够处理时间依赖的变量和约束。
内置求解器：GEKKO 有自己的内置求解器，同时也支持一些外部求解器。
模型预测控制（MPC）：GEKKO 提供了模型预测控制的功能，这在过程控制和工业自动化领域非常有用。
高层次的抽象：用户可以用较高层次的数学语言定义优化问题，无需深入了解底层的数学细节。
远程求解：GEKKO 支持将优化问题发送到远程服务器进行求解，这对于处理大规模或计算密集型问题特别有用。

应用领域

化工和过程工程：在化学反应工程、过程优化和系统设计中广泛应用。
能源管理：比如电力系统的优化、可再生能源系统的集成。
生物工程和制药：用于药物开发和生物过程的优化。
机械工程和设计：在机械系统的设计和优化中发挥作用。

GEKKO 的灵活性和强大的动态系统建模能力使其在工业优化和工程领域非常受欢迎。

参考链接：

使用scipy.optimize寻找函数最优解

scipy.optimize简介

scipy.optimize.minimize简介