先前按照Scikit-Learn的文档整理了一份评估指标,回头看下梳理的非常的技术化,整理完有种自己都不太想看的感觉。今天抽时间再做一次重新的梳理。
分类任务评估指标
混淆矩阵(Confusion Matrix)
分类任务的基础工具,用于统计预测结果与真实标签的对应关系。
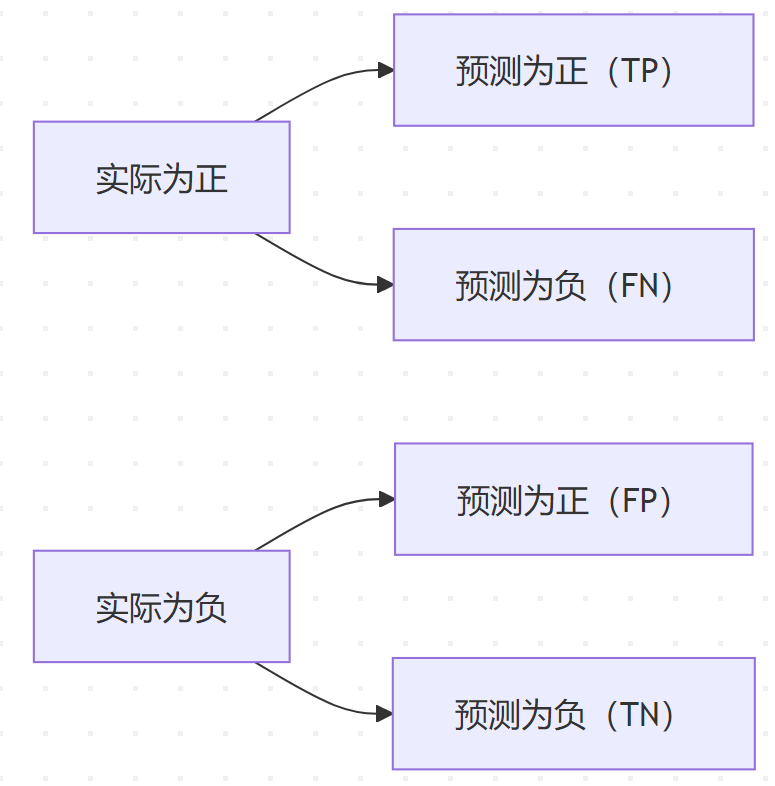
计算公式:
| 真实\预测 | 正类 (Positive) | 负类 (Negative) |
| 正类 | TP | FN |
| 负类 | FP | TN |
- TP(True Positive):实际为正,预测也为正。
- FN(False Negative):实际为正,但预测为负(漏报)。
- FP(False Positive):实际为负,但预测为正(误报)。
- TN(True Negative):实际为负,预测也为负。
核心指标
准确率(Accuracy)
- 定义:正确预测的比例
- 公式:$\text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN}$
- 适用场景:类别平衡时有效,类别不平衡时可能失效
精确率(Precision)
- 定义:预测为正类的样本中实际为正类的比例
- 公式:$\text{Precision} = \frac{TP}{TP + FP}$
- 适用场景:注重减少假正例(如垃圾邮件检测)
召回率(Recall/Sensitivity)
- 定义:实际为正类的样本中被正确预测的比例
- 公式:$\text{Recall} = \frac{TP}{TP + FN}$
- 适用场景:注重减少假反例(如疾病诊断)
F1-Score
- 定义:精确率和召回率的调和平均
- 公式:$F1 = \frac{2 \times \text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}$
- 适用场景:需要平衡精确率和召回率
进阶指标
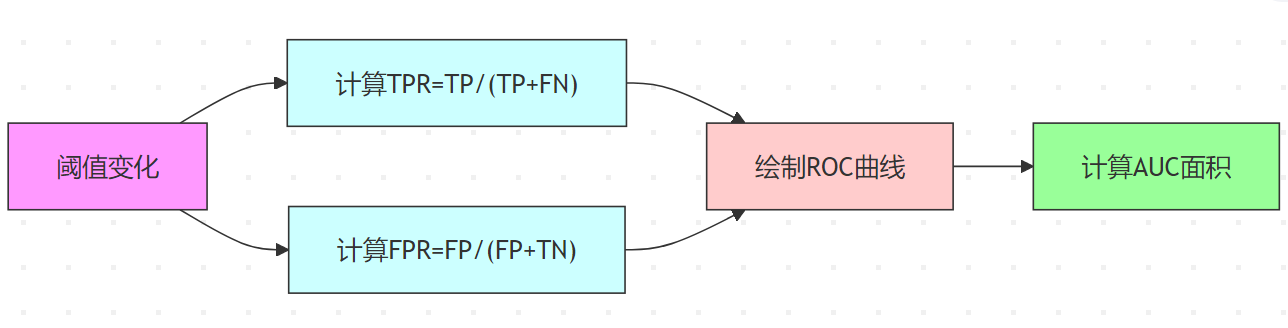
ROC曲线与AUC
- ROC曲线:显示不同阈值下TPR(True Positive Rate)与FPR(False Positive Rate)的关系
- AUC值:曲线下面积,反映分类器整体性能
PR曲线(Precision-Recall Curve)
- 适用场景:类别高度不平衡时比ROC更有效
- 横轴:召回率
- 纵轴:精确率
多分类指标
宏平均(Macro Average)
- 对每个类别单独计算指标后取平均
- 公式:$\text{Macro-Precision} = \frac{1}{N} \sum_{i=1}^N \text{Precision}_i$
微平均(Micro Average)
- 合并所有类别的统计量后计算指标
- 公式:$\text{Micro-Precision} = \frac{\sum TP}{\sum TP + \sum FP}$
指标对比场景
| 场景 | 推荐指标 |
| 类别平衡 | Accuracy, F1 |
| 类别高度不平衡 | Precision, Recall, AUC |
| 重视减少假阳性 | Precision |
| 重视减少假阴性 | Recall |
| 模型整体排序能力评估 | AUC |
Scikit-Learn实现
准备数据和模型
from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression # 生成二分类数据(类别不平衡) X, y = make_classification(n_samples=1000, weights=[0.9], flip_y=0.2, random_state=42) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) # 训练模型 model = LogisticRegression() model.fit(X_train, y_train) y_pred = model.predict(X_test) y_proba = model.predict_proba(X_test)[:, 1] # 概率预测(用于AUC)
核心指标计算
混淆矩阵
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay cm = confusion_matrix(y_test, y_pred) disp = ConfusionMatrixDisplay(cm) disp.plot() # 可视化
准确率
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.4f}")
精确率/召回率/F1
from sklearn.metrics import precision_score, recall_score, f1_score
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
print(f"Precision: {precision:.4f}, Recall: {recall:.4f}, F1: {f1:.4f}")
进阶指标计算
ROC与AUC
from sklearn.metrics import roc_curve, roc_auc_score
fpr, tpr, thresholds = roc_curve(y_test, y_proba)
auc = roc_auc_score(y_test, y_proba)
# 绘制ROC曲线
import matplotlib.pyplot as plt
plt.plot(fpr, tpr, label=f"AUC = {auc:.2f}")
plt.plot([0, 1], [0, 1], linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend()
plt.show()
PR曲线
from sklearn.metrics import precision_recall_curve
precision, recall, _ = precision_recall_curve(y_test, y_proba)
plt.plot(recall, precision)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.show()
多分类场景
# 生成多分类数据(3类)
X_multi, y_multi = make_classification(n_classes=3, n_clusters_per_class=1, random_state=42)
X_train_m, X_test_m, y_train_m, y_test_m = train_test_split(X_multi, y_multi, test_size=0.3)
model_multi = LogisticRegression()
model_multi.fit(X_train_m, y_train_m)
y_pred_multi = model_multi.predict(X_test_m)
# 宏平均 vs 微平均
macro_precision = precision_score(y_test_m, y_pred_multi, average='macro')
micro_precision = precision_score(y_test_m, y_pred_multi, average='micro')
print(f"Macro Precision: {macro_precision:.4f}, Micro Precision: {micro_precision:.4f}")
指标函数速查表
| 指标 | Scikit-Learn 函数 | 关键参数 |
| 混淆矩阵 | confusion_matrix | labels(指定类别顺序) |
| 准确率 | accuracy_score | normalize=False(返回数量) |
| 精确率/召回率 | precision_score/recall_score | average(宏/微/加权) |
| F1-Score | f1_score | average=’binary’(默认) |
| ROC曲线 | roc_curve | pos_label(指定正类) |
| AUC | roc_auc_score | multi_class=’ovr’(多类) |
| PR曲线 | precision_recall_curve | – |
分类报告(Classification Report)
Scikit-Learn的 classification_report 函数默认生成以下指标(按类别输出):
from sklearn.metrics import classification_report print(classification_report(y_true, y_pred))
- 精确率(Precision)
- 召回率(Recall)
- F1-Score
- 支持数(Support)
- 定义:测试集中每个类别的真实样本数量
- 意义:反映数据分布(识别类别不平衡问题)
- 平均值计算
- 宏平均(Macro Avg):各类别指标的算术平均
- 加权平均(Weighted Avg):按支持数加权的平均
- 准确率(Accuracy):总体的正确预测比例
注意事项
类别不平衡处理:
# 使用加权指标 weighted_f1 = f1_score(y_test, y_pred, average='weighted')
多分类AUC计算:
# One-vs-Rest策略计算AUC auc_ovr = roc_auc_score(y_test_multi, y_proba_multi, multi_class='ovr')
阈值调整:
# 根据业务需求调整分类阈值 y_pred_custom = (y_proba > 0.3).astype(int) # 默认阈值为0.5
通过 Scikit-Learn 的 metrics 模块可以快速实现所有主流分类指标的计算,建议结合交叉验证(如 cross_val_score)使用这些指标以获得更稳定的评估结果。
回归任务评估指标
核心指标解析

误差类指标
均方误差(MSE)
- 公式:$\text{MSE} = \frac{1}{n}\sum_{i=1}^{n}(y_i – \hat{y}_i)^2$
- 特点:
- 放大较大误差的影响(对异常值敏感)
- 量纲与原始数据平方相关(如预测房价时单位为万元²)
均方根误差(RMSE)
- 公式:$\text{RMSE} = \sqrt{\text{MSE}}$
- 特点:
- 恢复量纲(单位与原始数据一致)
- 比MSE更易解释(常见于Kaggle竞赛)
平均绝对误差(MAE)
- 公式:$\text{MAE} = \frac{1}{n}\sum_{i=1}^{n}|y_i – \hat{y}_i|$
- 特点:
- 对异常值更鲁棒
- 直观解释为平均预测偏差
关键指标对比
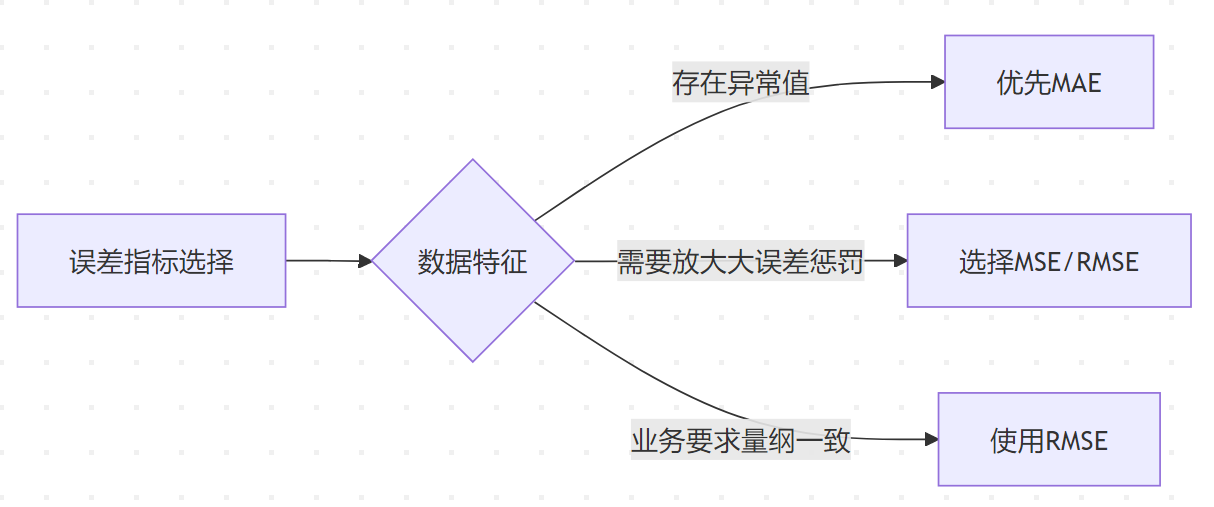
| 指标 | 异常值敏感性 | 量纲一致性 | 数学性质 |
| MSE | 高 | 否 | 可导,便于优化 |
| RMSE | 中 | 是 | 可导 |
| MAE | 低 | 是 | 不可导 |
相关性指标
决定系数(R²)
- 公式:$R^2 = 1 – \frac{\text{SSE}}{\text{SST}}$
- 范围:(-∞, 1]
- 1:完美拟合
- 0:等于基准模型(总是预测均值)
- 负数:模型差于基准模型
Pearson相关系数
公式:$r = \frac{\sum(x_i – \bar{x})(y_i – \bar{y})}{\sqrt{\sum(x_i – \bar{x})^2}\sqrt{\sum(y_i – \bar{y})^2}}$
特点:
- 衡量线性相关性(-1到1)
- 与R²的关系:$R^2 = r^2$(一元线性回归)
比例类指标
平均绝对百分比误差(MAPE)
- 公式:$\text{MAPE} = \frac{100\%}{n}\sum_{i=1}^{n}\left|\frac{y_i – \hat{y}_i}{y_i}\right|$
- 适用场景:
- 需求预测等需要相对误差的场景
- 当真实值接近零时失效(分母问题)
对称MAPE(SMAPE)
- 公式:$\text{SMAPE} = \frac{100\%}{n}\sum_{i=1}^{n}\frac{|y_i – \hat{y}_i|}{(|y_i| + |\hat{y}_i|)/2}$
- 特点:
- 解决MAPE的零值问题
- 结果可能超过100%
指标选择指南
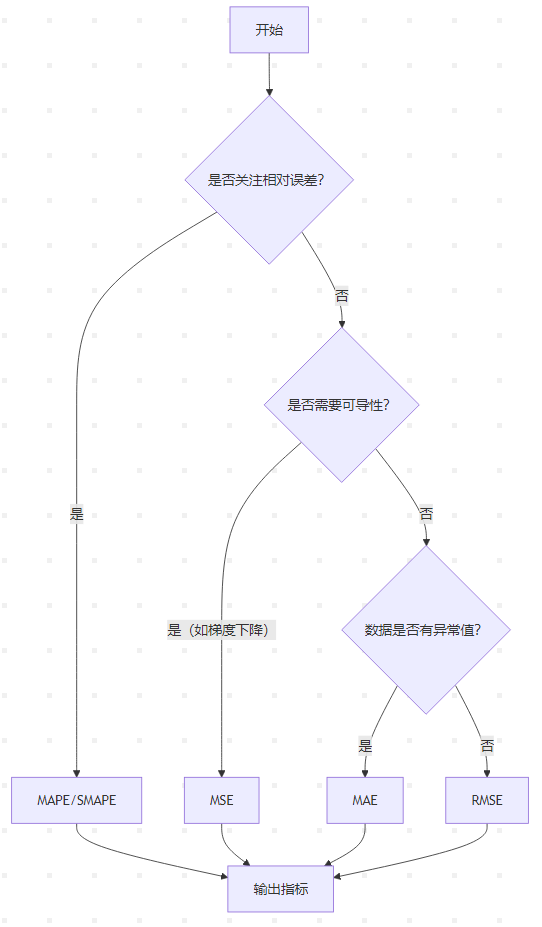
特殊场景处理
对数变换指标
- MSLE(Mean Squared Logarithmic Error):$\text{MSLE} = \frac{1}{n}\sum_{i=1}^{n}(\log(y_i + 1) – \log(\hat{y}_i + 1))^2$
- 适用场景:预测值范围大且呈指数分布(如用户增长量)
分位数损失

- 适用场景:需要预测区间估计(如金融风险控制)
核心公式关系
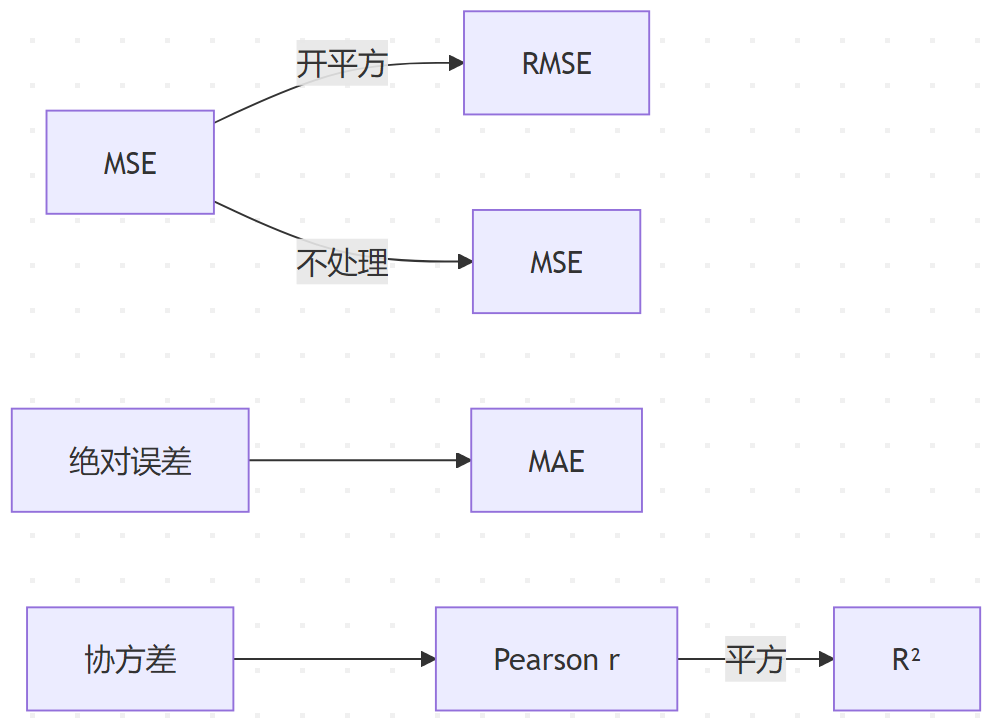
Scikit-Learn实现
Scikit-Learn内置指标
均方误差(MSE)和均方根误差(RMSE)
from sklearn.metrics import mean_squared_error
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
mse = mean_squared_error(y_true, y_pred) # MSE计算,默认squared=True
rmse = mean_squared_error(y_true, y_pred, squared=False) # RMSE计算
print(f"MSE: {mse:.2f}") # 输出 0.38
print(f"RMSE: {rmse:.2f}") # 输出 0.62
平均绝对误差(MAE)
from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(y_true, y_pred)
print(f"MAE: {mae:.2f}") # 输出 0.50
决定系数(R²)
from sklearn.metrics import r2_score
r2 = r2_score(y_true, y_pred)
print(f"R²: {r2:.2f}") # 输出 0.95
需自定义实现的指标
Pearson相关系数
使用numpy或scipy计算:
import numpy as np
from scipy.stats import pearsonr
# 方法1:numpy
r_np = np.corrcoef(y_true, y_pred)[0, 1]
# 方法2:scipy(同时返回p值)
r_scipy, p_value = pearsonr(y_true, y_pred)
print(f"Pearson (numpy): {r_np:.2f}") # 输出 0.93
print(f"Pearson (scipy): {r_scipy:.2f}") # 输出 0.93
平均绝对百分比误差(MAPE)
import numpy as np
def mape(y_true, y_pred):
# 避免除以零:移除真实值为零的样本
mask = y_true != 0
y_true = np.array(y_true)[mask]
y_pred = np.array(y_pred)[mask]
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
mape_val = mape(y_true, y_pred)
print(f"MAPE: {mape_val:.2f}%") # 输出 30.51%
对称平均绝对百分比误差(SMAPE)
def smape(y_true, y_pred):
denominator = (np.abs(y_true) + np.abs(y_pred)) / 2
# 避免分母为零:添加极小值
denominator = np.where(denominator == 0, 1e-10, denominator)
return np.mean(np.abs(y_pred - y_true) / denominator) * 100
smape_val = smape(y_true, y_pred)
print(f"SMAPE: {smape_val:.2f}%") # 输出 19.05%
完整代码示例
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import numpy as np
from scipy.stats import pearsonr
def regression_metrics(y_true, y_pred):
metrics = {}
# Scikit-Learn内置指标
metrics["MSE"] = mean_squared_error(y_true, y_pred)
metrics["RMSE"] = np.sqrt(metrics["MSE"])
metrics["MAE"] = mean_absolute_error(y_true, y_pred)
metrics["R²"] = r2_score(y_true, y_pred)
# Pearson相关系数
metrics["Pearson r"], _ = pearsonr(y_true, y_pred)
# 自定义指标(处理零值)
mask = np.array(y_true) != 0
y_true_filtered = np.array(y_true)[mask]
y_pred_filtered = np.array(y_pred)[mask]
if len(y_true_filtered) > 0:
metrics["MAPE"] = np.mean(np.abs((y_true_filtered - y_pred_filtered) / y_true_filtered)) * 100
else:
metrics["MAPE"] = np.nan
denominator = (np.abs(y_true) + np.abs(y_pred)) / 2
denominator = np.where(denominator == 0, 1e-10, denominator)
metrics["SMAPE"] = np.mean(np.abs(y_pred - y_true) / denominator) * 100
return metrics
# 示例数据
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
# 计算所有指标
results = regression_metrics(y_true, y_pred)
for key, value in results.items():
print(f"{key}: {value:.2f}")
输出结果:
MSE: 0.38 RMSE: 0.62 MAE: 0.50 R²: 0.95 Pearson r: 0.93 MAPE: 30.51 SMAPE: 19.05
注意事项
零值处理:
- MAPE在真实值为零时无定义,需过滤或填充极小值。
- SMAPE的分母可能为零,需添加极小值(如1e-10)避免除零错误。
多输出回归:
- 若预测多变量,设置multioutput参数:
mse_multi = mean_squared_error(y_true, y_pred, multioutput=’uniform_average’)
非线性和鲁棒性:
- MSE对异常值敏感,MAE更鲁棒。
- 对数变换(MSLE)适用于右偏数据:
msle = mean_squared_log_error(y_true, y_pred)
聚类任务评估指标
评估指标分类体系

核心内部指标
轮廓系数 (Silhouette Coefficient)
轮廓系数(Silhouette Coefficient) 是一种无监督聚类评估指标,通过衡量样本在所属簇内的凝聚度与相邻簇的分离度,综合评估聚类质量。其核心思想是:优秀的聚类应使样本与同簇样本相似度高(凝聚度高),且与其他簇样本差异明显(分离度高)。系数值范围在 [-1, 1]:
- 接近 1:样本聚类合理,簇内紧密、簇间远离。
- 接近 0:样本处于簇边界,聚类模糊。
- 接近 -1:样本可能被分配到错误簇。
数学公式
单个样本的轮廓系数:$s(i) = \frac{b(i) – a(i)}{\max\{a(i), b(i)\}}$
- a(i):样本i 到同簇其他样本的平均距离(凝聚度)。
- b(i):样本i 到最近其他簇所有样本的最小平均距离(分离度)。
全局轮廓系数:$\text{Silhouette Score} = \frac{1}{n} \sum_{i=1}^{n} s(i)$
- n:样本总数。
计算步骤
- 计算凝聚度a(i):对每个样本 i,计算其与同簇所有其他样本的欧氏距离平均值。
- 计算分离度b(i):对每个样本 i,计算其到每个其他簇的平均距离,取最小值。
- 计算单个样本得分s(i):根据公式 $s(i) = \frac{b(i) – a(i)}{\max\{a(i), b(i)\}}$。
- 全局平均:所有样本得分的均值即为数据集的轮廓系数。
核心特性
- 范围:[-1, 1],值越大越好。
- 优点:
- 无需真实标签,适用于无监督场景。
- 对任意形状的簇敏感(如流形结构)。
- 结果直观,可分析样本级别聚类质量。
- 缺点:
- 计算复杂度高$O(n^2)$,不适合超大规模数据。
- 高维数据中距离计算可能失效(需降维预处理)。
- 对噪声和离群点敏感。
注意事项
- 数据预处理:
- 标准化:基于距离的指标需消除量纲差异。
- 降维:高维数据建议使用PCA或t-SNE降低维度。
- 噪声处理:通过去噪算法(如DBSCAN)或离群点检测提升结果可靠性。
- 簇结构分析:结合轮廓系数分布图(silhouette_diagram)观察各簇质量。
扩展应用:轮廓系数分布图
from sklearn.metrics import silhouette_samples
import matplotlib.cm as cm
# 生成轮廓系数分布图
def plot_silhouette(X, labels, n_clusters):
plt.figure(figsize=(8, 6))
silhouette_avg = silhouette_score(X, labels)
sample_silhouette_values = silhouette_samples(X, labels)
y_lower = 10
for i in range(n_clusters):
ith_cluster_silhouette = sample_silhouette_values[labels == i]
ith_cluster_silhouette.sort()
size_cluster_i = ith_cluster_silhouette.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_clusters)
plt.fill_betweenx(np.arange(y_lower, y_upper),
0, ith_cluster_silhouette,
facecolor=color, edgecolor=color, alpha=0.7)
plt.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
y_lower = y_upper + 10
plt.axvline(x=silhouette_avg, color="red", linestyle="--")
plt.xlabel("轮廓系数值")
plt.ylabel("簇编号")
plt.title(f"轮廓系数分布图 (k={n_clusters}, 平均={silhouette_avg:.2f})")
plt.show()
# 示例:绘制k=3时的分布图
plot_silhouette(X, labels, n_clusters=3)
解读:各簇的轮廓系数分布越均匀且接近平均值(红色虚线),聚类质量越高。
Calinski-Harabasz指数
Calinski-Harabasz 指数(简称 CH 指数)是一种用于评估聚类质量的内部指标,通过衡量簇间离散度与簇内离散度的比值来量化聚类效果。其核心思想是:好的聚类应使簇内样本紧密聚集,簇间明显分离。该指数值越高,表示聚类效果越好。
数学公式
$$\text{CH} = \frac{\text{SS}_B / (k – 1)}{\text{SS}_W / (n – k)}$$
- $\text{SS}_B$(簇间离散度):各簇中心与全局中心距离的平方和,加权以簇的样本数。
- $\text{SS}_W$(簇内离散度):所有样本与其所属簇中心距离的平方和。
- k:簇的数量。
- n:样本总数。
计算步骤
- 计算全局中心:所有样本的均值点。
- 计算簇中心:每个簇内样本的均值点。
- 计算$\text{SS}_B$:$\text{SS}_B = \sum_{i=1}^{k} n_i \cdot \| \mathbf{c}_i – \mathbf{\mu} \|^2$
- $n_i$:第i 个簇的样本数。
- $\mathbf{c}_i$:第i 个簇的中心。
- $\mathbf{\mu}$:全局中心。
- 计算$\text{SS}_W$:$\text{SS}_W = \sum_{i=1}^{k} \sum_{\mathbf{x} \in C_i} \| \mathbf{x} – \mathbf{c}_i \|^2$
- $C_i$:第i 个簇的样本集合。
核心特性
- 范围:理论上无上限,值越大越好。
- 优点:
- 计算效率高,适合大规模数据集。
- 无需真实标签(无监督指标)。
- 对球形簇结构敏感,适合 K-means 等基于距离的算法。
- 缺点:
- 对非球形簇或复杂形状的簇效果较差。
- 高维数据中可能因“维度灾难”失效。
- 倾向于选择较大的k 值(需结合其他指标综合判断)。
注意事项
- 数据标准化:使用基于距离的算法(如 K-means)时,需对数据标准化。
- 高维数据:建议先降维(如 PCA)再计算 CH 指数。
- 非球形簇:若数据包含复杂形状簇,需结合轮廓系数或 DBCV 指数评估。
Davies-Bouldin指数 (DBI)
Davies-Bouldin指数(DBI) 是一种无监督聚类评估指标,通过衡量簇内样本的紧密度与簇间分离度的比值来量化聚类质量。其核心思想是:优秀的聚类应使簇内样本尽可能紧密,簇间尽可能远离。DBI值越小(最小为0),表示聚类效果越好。
数学公式
$$\text{DBI} = \frac{1}{k} \sum_{i=1}^{k} \max_{j \neq i} \left( \frac{\sigma_i + \sigma_j}{d(c_i, c_j)} \right)$$
- $\sigma_i$:簇i 内所有样本到其质心的平均距离(簇内离散度)。
- $d(c_i, c_j)$:簇i 和簇 j 质心之间的欧氏距离(簇间分离度)。
- k:簇的数量。
计算步骤
- 计算簇内离散度:对每个簇i,计算其样本到质心的平均距离 $\sigma_i$。
- 计算簇间分离度:对每对簇i 和 j,计算质心间距 $d(c_i, c_j)$。
- 计算相似度比值:对每个簇i,找到与其最相似的簇 j(即 $\frac{\sigma_i + \sigma_j}{d(c_i, c_j)} $最大的簇)。
- 取平均值:对所有簇的最相似度比值取平均,得到最终DBI值。
核心特性
- 范围:$[0, +\infty)$,值越小越好。
- 优点:
- 无需真实标签,适用于无监督场景。
- 计算复杂度低$(O(k^2))$,适合中等规模数据。
- 对任意形状的簇均适用。
- 缺点:
- 对簇的数量敏感,可能倾向于选择较少的簇。
- 高维数据中可能因距离计算失效(需结合降维处理)。
- 对噪声和异常值较为敏感。
注意事项
- 数据预处理:
- 标准化数据以避免量纲差异影响距离计算。
- 高维数据建议先降维(如PCA)再计算DBI。
- 噪声处理:DBI对噪声敏感,需通过去噪算法(如DBSCAN)预处理数据。
- 簇大小平衡:当簇大小差异显著时,DBI可能偏向于合并小簇。
关键外部指标
调整兰德指数 (Adjusted Rand Index, ARI)
调整兰德指数 (Adjusted Rand Index, ARI) 是一种用于评估聚类结果与真实标签一致性的外部指标,通过对比样本对的分配关系来量化预测标签与真实标签的相似性。其核心特点是对随机分配的校正,使得结果在 [-1, 1] 范围内可解释:
- 1:预测标签与真实标签完全一致。
- 0:预测标签与真实标签的匹配程度等同于随机分配。
- 负数:预测标签的匹配程度比随机分配更差。
数学原理
列联表与样本对统计,假设真实标签有 k 个类,预测标签有 m 个簇,构建列联表(Contingency Table)统计样本对的分配关系:
| 真实标签 \ 预测标签 | 簇1 | 簇2 | … | 簇m | 总计 |
| 类1 | n_{11} | n_{12} | … | n_{1m} | a_1 |
| 类2 | n_{21} | n_{22} | … | n_{2m} | a_2 |
| … | … | … | … | … | … |
| 类k | n_{k1} | n_{k2} | … | n_{km} | a_k |
| 总计 | b_1 | b_2 | … | b_m | n |
- $n_{ij}$:真实标签为类i 且预测标签为簇 j 的样本数。
- $a_i = \sum_{j=1}^m n_{ij}$:真实标签中类i 的样本数。
- $b_j = \sum_{i=1}^k n_{ij}$:预测标签中簇j 的样本数。
- $n = \sum_{i,j} n_{ij}$:总样本数。
样本对分类,所有样本对可分为四类:
- TP(True Positive):同一真实类且同一预测簇。
- FP(False Positive):不同真实类但同一预测簇。
- FN(False Negative):同一真实类但不同预测簇。
- TN(True Negative):不同真实类且不同预测簇。
兰德指数 (Rand Index, RI)
衡量预测标签与真实标签的一致性:$\text{RI} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{FP} + \text{FN} + \text{TN}}$
缺点:即使随机分配,RI值也可能较高(尤其在类别数或簇数较大时)。
调整兰德指数 (ARI),引入随机分配校正,公式为:
$$\text{ARI} = \frac{\text{RI} – E[\text{RI}]}{\max(\text{RI}) – E[\text{RI}]}$$
进一步推导为:
$$\text{ARI} = \frac{\sum_{ij} \binom{n_{ij}}{2} – \frac{\sum_i \binom{a_i}{2} \sum_j \binom{b_j}{2}}{\binom{n}{2}}}{\frac{1}{2} \left( \sum_i \binom{a_i}{2} + \sum_j \binom{b_j}{2} \right) – \frac{\sum_i \binom{a_i}{2} \sum_j \binom{b_j}{2}}{\binom{n}{2}}}$$
- $\binom{n}{2}$:样本对的组合数,即$\frac{n(n-1)}{2}$。
- 分子:实际一致的样本对数减去随机期望值。
- 分母:最大可能一致样本对数减去随机期望值。
核心特性
- 取值范围:[-1, 1],值越大越好。
- 对称性:$\text{ARI}(U, V) = \text{ARI}(V, U)$。
- 优点:
- 对类别不平衡鲁棒(如某些类样本极少)。
- 无需假设簇的形状或分布(适用于任意聚类算法)。
- 对随机分配进行了校正,结果更可靠。
- 缺点:
- 需要真实标签,仅适用于有监督验证。
- 计算复杂度较高(O(n^2)),不适合超大规模数据。
应用场景
- 有监督验证:当存在真实标签时,评估聚类质量。
- 算法对比:比较不同聚类算法(如K-means vs DBSCAN)的标签一致性。
- 超参数调优:选择使ARI最大化的最佳簇数或算法参数。
注意事项
- 标签独立性:ARI对标签排列不变(如交换簇编号不影响结果)。
- 零簇处理:若预测标签中某簇无样本(空簇),可能导致计算异常。
- 类别与簇数不等:允许真实类别数与预测簇数不同(如真实3类,预测4簇)。
归一化互信息 (Normalized Mutual Information, NMI)
归一化互信息(NMI) 是一种用于评估聚类结果与真实标签一致性的外部指标,衡量两个标签分配之间的相似性。其核心思想基于信息论中的互信息(Mutual Information, MI),通过归一化处理使得结果在 [0, 1] 范围内可解释。
数学原理
互信息(MI):表示两个随机变量之间的依赖程度,定义为:
$$I(U; V) = \sum_{u \in U} \sum_{v \in V} P(u, v) \log \frac{P(u, v)}{P(u)P(v)}$$
- U: 真实标签的分布
- V: 预测标签的分布
- P(u, v): 样本同时属于真实簇 u 和预测簇 v 的联合概率
- P(u), P(v) : 边缘概率(即簇占比)
熵(Entropy):描述标签分布的不确定性:
- 真实标签熵:$H(U) = -\sum_{u \in U} P(u) \log P(u)$
- 预测标签熵:$H(V) = -\sum_{v \in V} P(v) \log P(v)$
归一化方法:将互信息标准化以消除量纲影响,常见方法:
- 算术平均(默认):$\text{NMI} = \frac{2 \cdot I(U; V)}{H(U) + H(V)}$
- 几何平均:$\text{NMI} = \frac{I(U; V)}{\sqrt{H(U) H(V)}}$
- 最小值:$\text{NMI} = \frac{I(U; V)}{\min(H(U), H(V))}$
核心特性
- 取值范围:
- 1:预测标签与真实标签完全一致。
- 0:预测标签与真实标签完全独立(随机分配)。
- 优点:
- 对类别不平衡鲁棒(例如真实标签中某一类占多数)。
- 不受簇排列和标签编号影响(与ARI类似)。
- 缺点:
- 计算复杂度较高(需要遍历所有类别组合)。
- 在样本量较少时可能不够稳定。
应用场景
- 有监督验证:当存在真实标签时,评估聚类质量。
- 类别不平衡数据:真实标签中某些类别样本极少。
- 算法对比:比较不同聚类算法在相同数据集上的表现。
指标对比矩阵
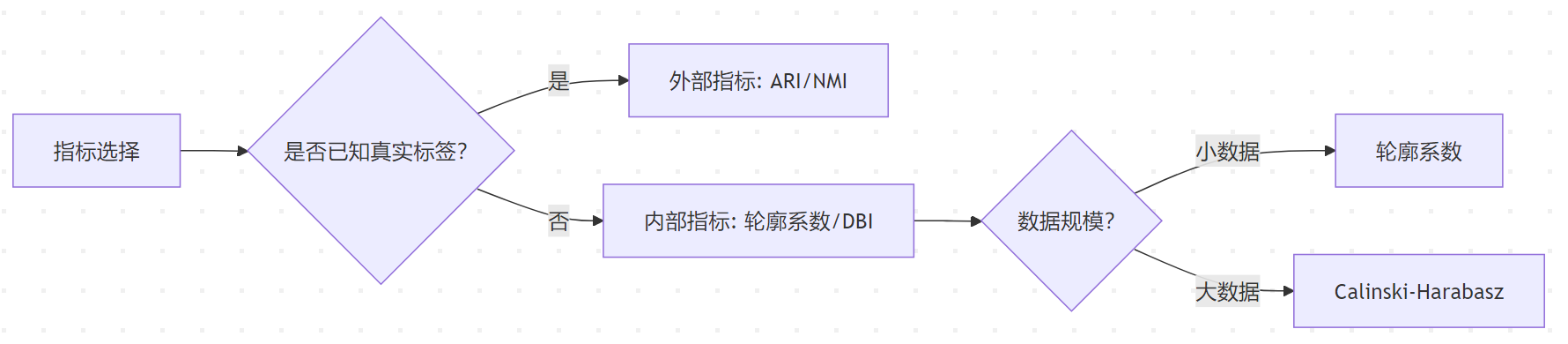
| 指标 | 需要标签 | 计算复杂度 | 最佳方向 | 适用场景 |
| 轮廓系数 | 否 | O(N²) | 越大越好 | 中小规模,形状复杂簇 |
| Calinski-Harabasz | 否 | O(NK) | 越大越好 | 大规模,凸簇 |
| DBI | 否 | O(K²) | 越小越好 | 任意规模,平衡簇大小 |
| ARI | 是 | O(N²) | 越大越好 | 有标签验证 |
| NMI | 是 | O(N²) | 越大越好 | 类别不平衡数据 |
特殊场景处理
非凸簇评估
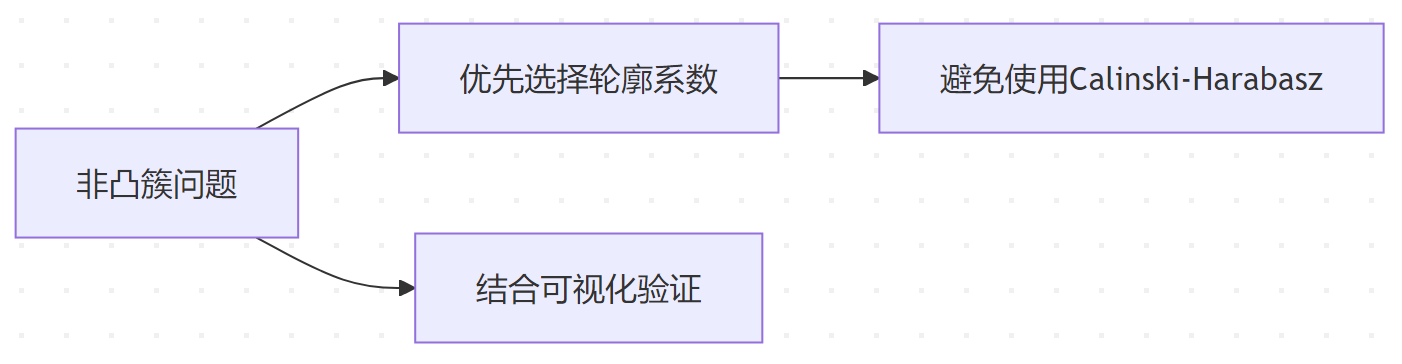
类别不平衡
高维数据

Scikit-Learn实现
内置的聚类评估指标
轮廓系数 (Silhouette Coefficient)
from sklearn.metrics import silhouette_score
# 输入:特征矩阵X和聚类标签labels
score = silhouette_score(X, labels)
print(f"轮廓系数: {score:.2f}")
- 参数说明:
- metric:距离度量(默认’euclidean’,可选’cosine’等)
- sample_size:大数据时抽样计算(提升速度)
- 适用场景:无标签数据,中小规模数据集
Calinski-Harabasz指数
from sklearn.metrics import calinski_harabasz_score
score = calinski_harabasz_score(X, labels)
print(f"Calinski-Harabasz指数: {score:.2f}")
- 特点:计算速度快,适合大规模数据和高维特征
Davies-Bouldin指数 (DBI)
from sklearn.metrics import davies_bouldin_score
score = davies_bouldin_score(X, labels)
print(f"Davies-Bouldin指数: {score:.2f}")
- 注意:值越小越好,0表示最优
调整兰德指数 (Adjusted Rand Index, ARI)
from sklearn.metrics import adjusted_rand_score
# 输入:真实标签true_labels和预测标签pred_labels
score = adjusted_rand_score(true_labels, pred_labels)
print(f"ARI: {score:.2f}")
- 适用场景:有真实标签的监督验证
归一化互信息 (Normalized Mutual Info, NMI)
from sklearn.metrics import normalized_mutual_info_score
score = normalized_mutual_info_score(true_labels, pred_labels)
print(f"NMI: {score:.2f}")
- 参数:
- average_method:聚合方法(默认’arithmetic’,可选’max’等)
完整代码示例
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import (
silhouette_score,
calinski_harabasz_score,
davies_bouldin_score,
adjusted_rand_score,
normalized_mutual_info_score
)
# 生成示例数据(带真实标签)
X, true_labels = make_blobs(n_samples=500, centers=3, random_state=42)
# 使用KMeans聚类
kmeans = KMeans(n_clusters=3, random_state=42)
pred_labels = kmeans.fit_predict(X)
# 计算内部指标
print(f"轮廓系数: {silhouette_score(X, pred_labels):.2f}") # 输出约0.79
print(f"Calinski-Harabasz指数: {calinski_harabasz_score(X, pred_labels):.2f}") # 输出约3000+
print(f"Davies-Bouldin指数: {davies_bouldin_score(X, pred_labels):.2f}") # 输出约0.35
# 计算外部指标(需真实标签)
print(f"ARI: {adjusted_rand_score(true_labels, pred_labels):.2f}") # 输出1.0(完美匹配)
print(f"NMI: {normalized_mutual_info_score(true_labels, pred_labels):.2f}") # 输出1.0
进阶使用技巧
不同距离度量的轮廓系数
# 使用余弦距离计算轮廓系数 score_cosine = silhouette_score(X, labels, metric='cosine') # 对稀疏数据使用曼哈顿距离 from scipy.sparse import csr_matrix X_sparse = csr_matrix(X) score_manhattan = silhouette_score(X_sparse, labels, metric='manhattan')
聚类稳定性评估
from sklearn.metrics.cluster import pair_confusion_matrix # 比较两次聚类结果的稳定性 labels1 = KMeans(n_clusters=3).fit_predict(X) labels2 = KMeans(n_clusters=3).fit_predict(X) confusion = pair_confusion_matrix(labels1, labels2)
自定义指标模板
from sklearn.metrics import make_scorer
from sklearn.model_selection import GridSearchCV
# 将DBI包装为Scorer(注意:DBI需要最小化)
dbi_scorer = make_scorer(davies_bouldin_score, greater_is_better=False)
# 用于GridSearchCV调参
param_grid = {'n_clusters': [2, 3, 4]}
grid = GridSearchCV(KMeans(), param_grid, scoring=dbi_scorer)
grid.fit(X)
print(f"最优参数: {grid.best_params_}") # 输出{'n_clusters': 3}
性能优化策略
大数据集抽样计算
# 仅用前200个样本计算轮廓系数 sample_indices = np.random.choice(len(X), 200, replace=False) score = silhouette_score(X[sample_indices], labels[sample_indices])
并行加速
# 使用joblib并行计算(需安装joblib)
from joblib import Parallel, delayed
def parallel_silhouette(X, labels, n_jobs=-1):
samples = [X[i] for i in range(len(X))]
return Parallel(n_jobs=n_jobs)(
delayed(silhouette_samples)(samples, labels)
)
常见问题解答
Q1:为什么轮廓系数为负数?
可能原因:聚类结果差于随机分配,检查数据预处理或调整聚类算法
Q2:如何解释Calinski-Harabasz的高值?
该值没有上限,需通过对比不同聚类数结果判断最优:
for k in range(2, 6):
labels = KMeans(n_clusters=k).fit_predict(X)
score = calinski_harabasz_score(X, labels)
print(f"k={k}: {score:.1f}")
Q3:NMI和ARI的区别?
- NMI对类别不平衡更鲁棒
- ARI对完全随机结果的期望值为0,更易解释