对于数据科学家程序员而言,为工作选择正确的数据结构至关重要。特别是,如果算法需要大量计算,例如训练机器学习模型的算法或处理大量数据的算法,那么确保选择合适的数据结构时要特别小心。选择正确的数据类型通常会被忽略,并且最终会严重影响应用程序的性能。

在编程过程中,不同的数据代表着不一样的作用,并且他们的执行效率也会不一样。
Big-O表示法
在算法中执行许多操作。这些操作可能包括遍历集合,复制项目或整个集合,将项目追加到集合中,在集合的开始或结尾处插入项目,删除项目或更新集合中的项目。Big-O衡量算法运算的时间复杂度。它测量算法计算所需运算所需的时间。尽管我们也可以测量空间复杂度(算法占用多少空间),但本文将重点介绍时间复杂度。用最简单的术语来说,BigO表示法是一种基于输入大小(称为n)来衡量操作性能的方法。
让我们考虑n为输入集合的大小。
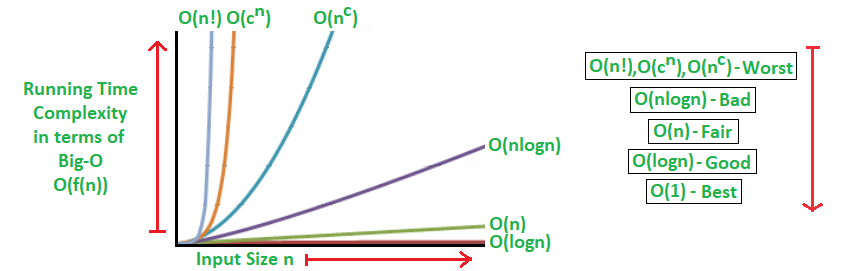
就时间复杂度而言:
- O(1):无论您的集合有多大,执行操作所花费的时间都是恒定的。这是恒定的时间复杂度符号。这些操作尽可能快。例如,检查集合内部是否有任何项目的操作是O(1)操作。
- O(log n):当集合的大小增加时,执行操作所花费的时间对数增加。这是对数时间复杂度表示法。潜在优化的搜索算法为O(log n)。
- O(n):执行操作所需的时间与集合中的项目数成线性正比。这是线性时间复杂度符号。就性能而言,这介于两者之间或中等。作为一个实例,如果我们想对一个集合中的所有项目求和,那么我们将不得不遍历该集合。因此,集合的迭代是O(n)操作。
- O(n log n):执行某项操作的性能是集合中项目数量的拟线性函数。这称为准线性时间复杂度表示法。优化排序算法的时间复杂度通常为n(log n)。
- O(n^2):执行操作所需的时间与集合中项目的平方成正比。这称为二次时间复杂度表示法。
- O(n!):当在操作中计算集合的每个单个排列时,因此执行操作所需的时间取决于集合中项目的大小。这称为阶乘时间复杂度表示法。非常慢。
该图像概述了Big-O符号:
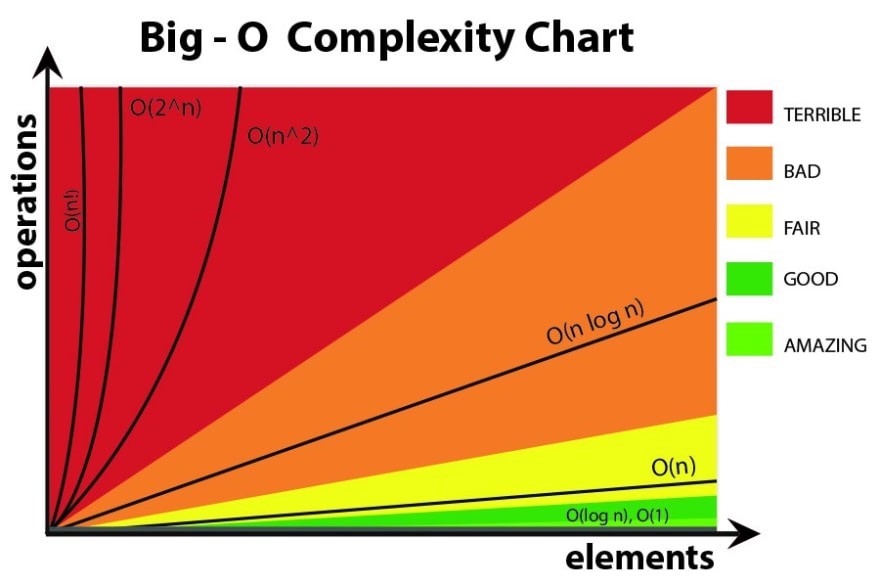
大O符号是相对的。大O表示法与机器无关,忽略常量,并且被包括数学家,技术人员,数据科学家等在内的广泛读者所理解。
最佳,平均,最差情况
当我们计算操作的时间复杂度时,我们可以根据最佳,平均或最坏情况产生复杂度。
- 最佳情况方案:顾名思义,这是当数据结构和集合中的项目以及参数处于最佳状态时的方案。例如,假设我们要在集合中找到一个项目。如果该项目恰好是集合的第一项,那么这是该操作的最佳情况。
- 平均情况是根据输入值的分布定义复杂度。
- 最坏的情况是可能需要一种操作,该操作需要在大型集合(例如列表)中找到位于最后一个项目的项目,并且算法会从第一个项目开始对集合进行迭代。
Python内置方法的时间复杂度
List列表
以完全随机的列表考虑平均情况。Python的列表内部实现是数组列表是以数组(Array)。最大的开销发生在超过当前分配大小的增长,这种情况下所有元素都需要移动;或者是在起始位置附近插入或者删除元素,这种情况下所有在该位置后面的元素都需要移动。如果你需要在一个队列的两端进行增删的操作,应当使用collections.deque(双向队列)
| 操作 | 案例 | 类型 | 备注 |
| Index | l[i] | O(1) | |
| Store | l[i]=0 | O(1) | |
| Length | len(l) | O(1) | |
| Append | l.append(5) | O(1) | |
| Pop | l.pop() | O(1) | l.pop(-1)同理 |
| Clear | l.clear() | O(1) | l=[]同理 |
| Slice | l[a:b] | O(b-a) | l[1:5]:O(l)/l[:]:O(len(l)-0)=O(N) |
| Extend | l.extend(…) | O(len(…)) | 取决于…的长度 |
| Construction | list(…) | O(len(…)) | 取决于…的长度 |
| Insert | l.insert(1) | O(N) | |
| Pop | l.pop(i) | O(N) | O(N-i):l.pop(0):O(N)(see above) |
| check ==,!= | l1==l2 | O(N) | |
| Insert | l[a:b]=… | O(N) | |
| Delete | del l[i] | O(N) | 取决于i的位置,最坏的情况为O(N) |
| Containment | x in/not in l | O(N) | 需逐个查找导致 |
| Copy | l.copy() | O(N) | l[:]同理 |
| Remove | l.remove(…) | O(N) | |
| Extreme value | min(l)/max(l) | O(N) | 需逐个查找导致 |
| Reverse | l.reverse() | O(N) | |
| Iteration | for v in l: | O(N) | 当循环中没有return或break的时候,为O(N) |
| Sort | l.sort() | O(NLogN) | |
| Multiply | k * l | O(kN) |
dict字典及defaultdict默认字典
关于字典需要了解的是hash函数和哈希桶。一个好的hash函数使到哈希桶中的值只有一个,若多个key hash到了同一个哈希桶中,称之为哈希冲突。查找值时,会先定位到哈希桶中,再遍历hash桶。更详细的信息请点这里。在hash基本没有冲突的情况下get, set, delete, in方面都是O(1)。
| 操作 | 案例 | 类型 | 备注 |
| Index | d[k] | O(1) | |
| Store | d[k] = v | O(1) | |
| Length | len(d) | O(1) | |
| Delete | del d[k] | O(1) | |
| get/setdefault | d.get(k) | O(1) | |
| Pop | d.pop(k) | O(1) | |
| Popitem | d.popitem() | O(1) | |
| Clear | d.clear() | O(1) | 与 s={} 或 s=dict() 同理 |
| View | d.keys() | O(1) | 与 d.values() 同理 |
| Construction | dict(…) | O(len(…)) | |
| Iteration | for k in d: | O(N) | 包含以下方法:keys, values, items |
Set集合
集合也是Python中使用最广泛的数据集合之一。集合本质上是无序集合。集合不允许重复,因此集合中的每个项目都是唯一的。集合支持许多数学运算,例如联合,差,集合的交集等。内部实现是dict的。在in操作上是O(1),这一点比list要强。
| 操作 | 案例 | 类型 | 备注 |
| Length | len(s) | O(1) | |
| Add | s.add(5) | O(1) | |
| Containment | x in/not in s | O(1) | 对比list/tuple的O(N)快很多 |
| Remove | s.remove(..) | O(1) | compare to list/tuple – O(N) |
| Discard | s.discard(..) | O(1) | |
| Pop | s.pop() | O(1) | popped value “randomly” selected |
| Clear | s.clear() | O(1) | 与 s=set() 同理 |
| Construction | set(…) | O(len(…)) | 取决于…的长度 |
| check ==, != | s != t | O(len(s)) | 与 len(t) 同理 |
| <= / < | s <= t | O(len(s)) | 类似issubset方法 |
| >= / > | s >= t | O(len(t)) | |
| Union | s | t | O(len(s)+len(t)) | |
| Intersection | s & t | O(len(s)+len(t)) | |
| Difference | s – t | O(len(s)+len(t)) | |
| SymmetricDiff | s ^ t | O(len(s)+len(t)) | |
| Iteration | for v in s: | O(N) | 当循环中没有return或break的时候,为O(N) |
| Copy | s.copy() | O(N) |
collections.deque双向队列
deque(double-ended queue,双向队列)是以双向链表的形式实现的(Well, a list of arrays rather than objects, for greater efficiency)。双向队列的两端都是可达的,但从查找队列中间的元素较为缓慢,增删元素就更慢了。
| 操作 | 案例 | 类型 | 备注 |
| Copy | dq.copy() | O(n) | |
| append | dq.append(5) | O(1) | |
| appendleft | dq.appendleft(1) | O(1) | 作用相当于list.insert(0, 1), 但后者效率为O(N) |
| pop | dq.pop() | O(1) | |
| popleft | dq.popleft() | O(1) | |
| extend | dq.extend(k) | O(len(k)) | |
| extendleft | dq.extendleft(k) | O(len(k)) | |
| rotate | dq.rotate(k) | O(len(k)) | |
| remove | dq.remove(1) | O(n) |
参考链接:



