关于生存分析,先前已经整理过一篇非常详细的文章:生存分析从概念到实战,里面也涉及到了 lifelines 的使用。本次梳理期望从另外的层面对生存分析的使用进行进一步的梳理。
Lifelines 简介
lifelines 是一个专注于生存分析的 Python 库,适用于处理包含时间至事件的数据(如患者存活时间、设备故障时间等),尤其支持右截尾(censored)数据的分析。它提供了丰富的统计模型、可视化工具和评估方法,广泛应用于医学、工程、社会科学等领域。
主要功能
- 非参数模型:
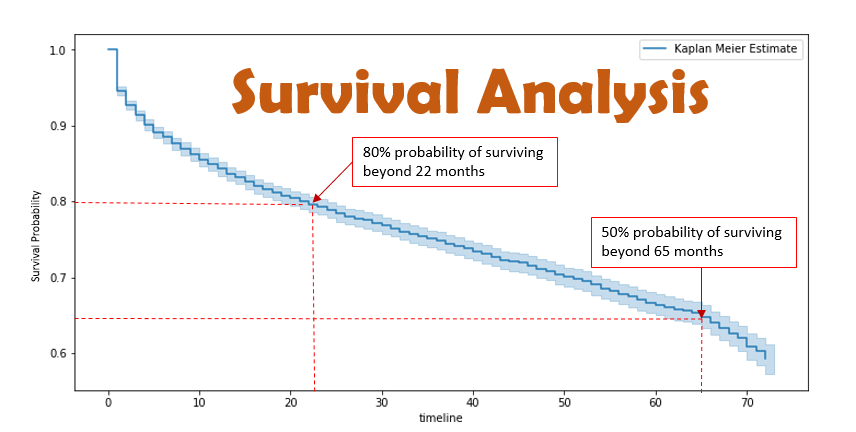
- Kaplan-Meier 估计器:用于估计生存函数,支持绘制生存曲线。
- Nelson-Aalen 估计器:估计累积风险函数。
- 半参数模型:
- Cox 比例风险模型(CoxPH):分析协变量对生存时间的影响,支持处理分层数据和时变变量。
- 参数模型:
- 支持指数分布、威布尔分布、对数正态分布等,通过最大似然估计拟合生存时间分布。
- 统计检验:
- Log-rank 检验:比较两组或多组生存曲线差异。
- 比例风险假设检验:验证 Cox 模型假设是否成立。
- 实用工具:
- 数据预处理(如截尾标记、时间变量处理)。
- 模型评估指标(AIC、BIC、Concordance Index)。
- 生存函数预测、中位生存时间计算。
高级功能
- 时变协变量:通过 add_covariate_to_timeline 处理动态变量。
- 分层分析:在 Cox 模型中对特定变量分层,缓解比例风险假设压力。
- 竞争风险:支持分析多事件类型(如 CompetingRiskFitter)。
注意事项
- 数据格式:
- 时间列应为非负数,事件列标记为 1(事件发生)或 0(截尾)。
- 分类变量需预先编码(如 get_dummies)。
- 模型假设检验:
- 使用 check_assumptions() 验证 Cox 模型的比例风险假设,若不满足可通过添加时变交互项或换用参数模型。
- 缺失值处理:需手动剔除或填充缺失值,否则模型报错。
Lifelines 的实现原理
lifelines 的核心目标是简化生存分析的建模流程,同时兼顾灵活性和计算效率。其实现逻辑基于生存分析的理论框架,通过统计模型和优化算法处理时间至事件数据(包含右截尾)。
数据结构的处理
输入格式:
要求数据为 DataFrame 或 numpy 数组,包含两列关键信息:
- duration_col:时间列(非负值,表示观察到事件发生或截尾的时间)。
- event_col:事件列(1 表示事件发生,0 表示右截尾)。
预处理:
- 自动检测并处理缺失值(需用户提前填充或删除)。
- 分类变量需转换为数值(例如使用 get_dummies)。
- 对时间变量排序,以支持非参数模型的逐步计算(如 Kaplan-Meier)。
非参数模型:Kaplan-Meier 估计器
数学原理:
生存函数 $S(t)$ 估计为:
$$S(t)=\prod_{t_i\leq t}(1-\frac{d_i}{n_i})$$
其中 $d_i$ 是时间 $t_i$ 处的事件数 $n_i$ 是该时间点前仍存活的个体数。
实现逻辑:
- 将数据按时间升序排列,统计每个时间点的事件数和风险集大小。
- 递推计算每个时间点的生存概率(累积乘积)。
- 支持右截尾数据:截尾个体在截尾时间后不再计入风险集。
- 使用插值方法生成平滑的生存曲线(如 plot_survival_function)。
代码优化:
利用 numpy 的向量化操作加速累积乘积计算,避免显式循环。
半参数模型:Cox 比例风险模型(CoxPH)
数学原理:
风险函数为:
$$h(t|x)=h_0(t)\exp(\beta^Tx)$$
其中 $h_0(t)$ 是基线风险函数,$\beta$ 是协变量系数,通过偏似然估计法(Partial Likelihood)求解。
偏似然函数:
对每个事件时间 $t_i$,计算其条件概率:
$$L(\beta)=\prod_{i=1}^D\frac{\exp(\beta^Tx_i)}{\sum_{j\in R(t_i)}\exp(\beta^Tx_j)}$$
其中 $R(t_i)$ 是时间 $t_i$ 处的风险集,$D$ 是事件总数。
实现逻辑:
- 偏似然最大化:使用牛顿-拉夫森法或拟牛顿法(如 BFGS)优化对数偏似然函数。
- 处理 ties(同时发生的事件):
- Breslow 方法(默认):近似处理,假设事件在同一时间点顺序发生。
- Efron 方法:更精确但计算量更大。
- 正则化:支持 L1/L2 正则化(通过 penalizer 参数)。
- 时变协变量:通过扩展数据格式(add_covariate_to_timeline)动态更新协变量值。
代码实现:
- 依赖 autograd 或 scipy 库计算梯度与海森矩阵。
- 使用矩阵运算加速协变量与系数的乘法(例如 dot)。
参数模型(如 WeibullFitter)
数学原理:
假设生存时间服从特定分布(如威布尔分布),其生存函数为:
$$S(t)=\exp\left(-\left(\frac{t}{\lambda}\right)^\rho\right)$$
其中 $\lambda$ 和 $\rho$ 为形状参数,通过最大似然估计(MLE)求解。
似然函数:
对每个个体 $i$,似然贡献为:
$$L_i=\begin{cases}f(t_i)&\text{事件发生}\\S(t_i)&\text{右截尾}\end{cases}$$
总对数似然为 $\log L=\sum\log L_i$。
实现逻辑:
- 定义分布的概率密度函数(PDF)和生存函数(SF)。
- 使用 optimize 中的数值优化算法(如 minimize)最大化对数似然。
- 支持多种分布:指数分布(ExponentialFitter)、对数正态分布(LogNormalFitter)等。
统计检验与模型评估
- Log-Rank检验:
- 原理:比较两组生存曲线的差异,原假设为两组生存分布相同。
- 实现:计算观察事件数与期望事件数的卡方统计量:$\chi^2=\frac{(O-E)^2}{\text{Var}(O-E)}$
- 依赖 statistics 模块中的矩阵运算。
- 比例风险假设检验:
- Schoenfeld 残差检验:检验协变量效应是否随时间变化。
- 若残差与时间显著相关,则比例风险假设可能不成立。
- 模型评估:
- Concordance Index:衡量模型预测风险排序的能力。
- AIC/BIC:基于对数似然和参数数量评估模型复杂度。
可视化与输出
- 生存曲线绘制:
- 使用 matplotlib 生成生存函数、累积风险函数图。
- 支持自定义置信区间(通过 confidence_interval 参数)。
- 模型摘要:
- 输出系数估计、标准误、p 值、置信区间(如 print_summary())。
- 依赖 pandas 格式化输出表格。
性能优化
- 矩阵运算:利用 numpy 和 scipy 的向量化操作替代循环,加速大规模数据计算。
- 稀疏矩阵:对高维数据(如分层 Cox 模型)使用稀疏矩阵存储。
- 并行计算:部分模块(如交叉验证)支持多进程加速。
关键代码结构
- 模型基类:
- BaseFitter:定义通用方法(如 fit, plot)。
- RegressionFitter:扩展至回归模型(如 CoxPH、参数模型)。
- 生存函数计算:
- survival_function_ 属性存储生存概率,通过插值生成连续曲线。
- 参数估计:
- 在 _fit_model 方法中调用优化器(如 optimize)。
Lifeline 使用案例
案例1:医疗领域-癌症患者生存分析
背景:分析癌症患者的生存时间与治疗方式、年龄的关系。
数据:包含生存时间(月)、是否死亡(事件)、年龄、治疗方案(A/B)。
代码实现:
import pandas as pd
from lifelines import KaplanMeierFitter, CoxPHFitter
import matplotlib.pyplot as plt
# 示例数据
data = pd.DataFrame({
'time': [15, 30, 12, 24, 36, 8, 20, 10],
'event': [1, 1, 0, 1, 0, 1, 1, 0],
'age': [55, 68, 42, 70, 35, 60, 75, 50],
'treatment': ['A', 'B', 'A', 'B', 'A', 'B', 'A', 'B']
})
# 分类变量编码(如治疗方案)
data = pd.get_dummies(data, columns=['treatment'], drop_first=True)
# Kaplan-Meier 分析(按治疗方案分组)
kmf = KaplanMeierFitter()
for treatment in ['A', 'B']:
mask = data[f'treatment_{treatment}'] == 1 if treatment != 'A' else data['treatment_B'] == 0
kmf.fit(data[mask]['time'], event_observed=data[mask]['event'], label=f"Treatment {treatment}")
kmf.plot_survival_function()
plt.title('Survival by Treatment')
plt.xlabel('Time (Months)')
plt.ylabel('Survival Probability')
plt.show()
# Cox 比例风险模型
cph = CoxPHFitter()
cph.fit(data, duration_col='time', event_col='event', formula='age + treatment_B')
cph.print_summary()
结果解读:
- Kaplan-Meier 曲线:比较治疗方案 A 和 B 的生存概率差异。
- Cox 模型:输出 age 和 treatment_B 的风险比(HR),例如:
- treatment_B 的 HR<1 表示治疗方案 B 降低死亡风险。
- age 的 HR>1 表示年龄增加导致风险上升。
案例2:金融领域-客户流失预测
背景:预测客户流失时间与客户属性(如消费金额、活跃天数)的关系。
数据:包含流失时间(天)、是否流失(事件)、月均消费、活跃天数。
代码实现:
from lifelines import WeibullFitter
from lifelines.statistics import logrank_test
# 示例数据
data = pd.DataFrame({
'time': [90, 120, 60, 180, 30, 150, 45, 200],
'event': [1, 1, 1, 0, 1, 0, 1, 0],
'monthly_spend': [200, 500, 150, 800, 100, 600, 80, 300],
'active_days': [15, 30, 10, 25, 5, 20, 8, 18]
})
# 参数模型(Weibull 分布)
wf = WeibullFitter()
wf.fit(data['time'], event_observed=data['event'])
wf.plot_survival_function()
plt.title('Weibull Survival Curve for Customer Churn')
plt.show()
# Log-Rank 检验(按高/低消费分组)
high_spend = data['monthly_spend'] > 300
results = logrank_test(
data[high_spend]['time'],
data[~high_spend]['time'],
event_observed_A=data[high_spend]['event'],
event_observed_B=data[~high_spend]['event']
)
print(results.p_value) # p<0.05 表示两组流失率差异显著
结果解读:
- Weibull 模型:估计客户流失时间的分布形状(参数 rho 和 lambda)。
- Log-Rank 检验:验证高消费客户与低消费客户的流失率是否显著不同。
案例3:工程领域-设备故障时间预测
背景:分析设备故障时间与运行温度、维护次数的关系。
数据:包含故障时间(小时)、是否故障(事件)、温度、维护次数。
代码实现:
from lifelines import CoxPHFitter
from lifelines.utils import k_fold_cross_validation
# 示例数据
data = pd.DataFrame({
'time': [500, 800, 300, 1200, 600, 400, 900, 200],
'event': [1, 1, 1, 0, 1, 0, 1, 1],
'temperature': [85, 90, 75, 95, 80, 70, 88, 82],
'maintenance': [2, 3, 1, 4, 2, 1, 3, 0]
})
# Cox模型交叉验证
scores = k_fold_cross_validation(
CoxPHFitter(penalizer=0.1),
data,
duration_col='time',
event_col='event',
k=3,
scoring='concordance_index'
)
print(f"平均Concordance Index: {scores.mean()}")
# 拟合完整模型
cph = CoxPHFitter(penalizer=0.1)
cph.fit(data, duration_col='time', event_col='event')
cph.plot_partial_effects('temperature', values=[70, 80, 90])
plt.title('Temperature Effect on Hazard Ratio')
plt.show()
结果解读:
- 交叉验证:评估模型的泛化性能(Concordance Index越接近1,模型越好)。
- 部分效应图:显示温度对风险比的非线性影响(如高温显著增加故障风险)。
案例4:市场营销-用户订阅持续时间分析
背景:分析用户订阅时长与注册渠道、首次消费金额的关系。
数据:包含订阅时长(天)、是否取消订阅(事件)、注册渠道、首次消费金额。
代码实现:
from lifelines import KaplanMeierFitter
from lifelines import CoxTimeVaryingFitter
# 示例数据(时变协变量:用户每月消费金额)
data_long = pd.DataFrame({
'id': [1, 1, 2, 2, 3, 3],
'start': [0, 30, 0, 30, 0, 30],
'stop': [30, 60, 30, 60, 30, 45],
'event': [0, 1, 0, 0, 1, 1],
'monthly_spend': [50, 30, 100, 80, 20, 0],
'channel': ['organic', 'organic', 'paid', 'paid', 'organic', 'organic']
})
# 时变Cox模型
ctv = CoxTimeVaryingFitter()
ctv.fit(data_long, id_col='id', event_col='event', start_col='start', stop_col='stop')
ctv.print_summary()
# 按注册渠道分组的生存曲线
kmf = KaplanMeierFitter()
for channel in ['organic', 'paid']:
mask = data_long['channel'] == channel
kmf.fit(data_long[mask]['stop'], event_observed=data_long[mask]['event'], label=channel)
kmf.plot_survival_function()
plt.title('Subscription Survival by Channel')
plt.show()
结果解读:
- 时变协变量模型:分析用户每月消费金额变化对流失风险的动态影响。
- 生存曲线:比较不同注册渠道用户的订阅持续时间差异。
高级案例:竞争风险分析
背景:分析患者可能经历多类事件(如死亡、康复)的竞争风险。
数据:包含时间、事件类型(0=截尾,1=死亡,2=康复)、年龄。
代码实现:
from lifelines import CompetingRiskFitter
# 示例数据
data = pd.DataFrame({
'time': [10, 20, 15, 30, 25],
'event': [1, 2, 0, 1, 2],
'age': [60, 45, 70, 55, 50]
})
# 竞争风险模型(仅适用于单一协变量)
crf = CompetingRiskFitter()
crf.fit(data['time'], data['event'], data[['age']])
crf.plot_cumulative_incidence()
plt.show()
结果解读:
- 累积发病率曲线:展示不同事件(死亡、康复)随时间累积发生的概率。
参考链接:



