在程序开发中，我们常遇到用树型结构来表示某些数据间的关系，如企业的组织架构、商品的分类、操作栏目等，目前的关系型数据库都是以二维表的形式记录存储数据，而树型结构的数据如需存入二维表就必须进行Schema设计。最近对此方面比较感兴趣，专门做下梳理，如下为常见的树型结构的数据：
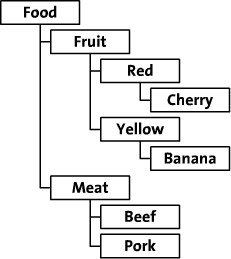
邻接列表模式AdjacencyList
最简单的方法是：AdjacencyList（邻接列表模式）。简单的说是根据节点之间的继承关系，显现的描述某一节点的父节点，从而建立二位的关系表。表结构通常设计为{Node_id, Parent_id}，如下图：
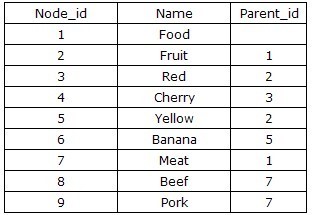
使用连接表的大致代码：
<?php
// $parent is the parent of the children we want to see
// $level is increased when we go deeper into the tree,
// used to display a nice indented tree
function display_children($parent, $level)
{
// 获得一个父节点$parent的所有子节点
$result = mysql_query('SELECT name FROM tree WHERE parent="'.$parent.'";');
// 显示每个子节点
while ($row = mysql_fetch_array($result))
{
// 缩进显示节点名称
echo str_repeat(' ', $level).$row['name']."\n";
// 再次调用这个函数显示子节点的子节点
display_children($row['name'], $level+1);
}
}
?>
对整个结构的根节点（Food）使用这个函数就可以打印出整个多级树结构，由于Food是根节点它的父节点是空的，所以这样调用: display_children(”, 0)。将显示整个树的内容。如果你只想显示整个结构中的一部分，比如说水果部分，就可以这样调用：display_children(‘Fruit’, 0);
几乎使用同样的方法我们可以知道从根节点到任意节点的路径。比如Cherry的路径是 ”Food>;Fruit>;Red”。为了得到这样的一个路径我们需要从最深的一级”Cherry”开始，查询得到它的父节点”Red”把它添加到路径中，然后我们再查询Red的父节点并把它也添加到路径中，以此类推直到最高层的”Food”
以下是代码：
<?php
// $node是那个最深的节点
function get_path($node)
{
// 查询这个节点的父节点
$result = mysql_query('SELECT parent FROM tree'.
'WHERE name="'.$node.'";');
$row = mysql_fetch_array($result);
// 用一个数组保存路径
$path = array();
// 如果不是根节点则继续向上查询
// (根节点没有父节点)
if ($row['parent'] != '')
{
// the last part of the path to $node, is the name
// of the parent of $node
$path[] = $row['parent'];
// we should add the path to the parent of this node
// to the path
$path = array_merge(get_path($row['parent']), $path);
}
// return the path
return $path;
}
?>
如果对”Cherry”使用这个函数：print_r(get_path(‘Cherry’))，就会得到这样的一个数组了：
Array ( [0] =>; Food [1] =>; Fruit [2] =>; Red )
这种方案的优点很明显：结构简单易懂，由于互相之间的关系只由一个parent_id维护，所以增删改都是非常容易，只需要改动和他直接相关的记录就可以。缺点当然也是非常的突出：由于直接地记录了节点之间的继承关系，因此对Tree的任何CRUD操作都将是低效的，这主要归根于频繁的“递归”操作，递归过程不断地访问数据库，每次数据库IO都会有时间开销。举个例子，如果想要返回所有水果，也就是水果的所有子孙节点，看似很简单的操作，就需要用到一堆递归。当然，这种方案并非没有用武之地，在树的层级比较少的时候就非常实用，在邻接列表模式的基础上还可以拓展的是平面表，区别是将节点的level和当前节点的顺序也放入表中，比较适合类似评论等场景，具体的表结构类似这样，这里就不再深入阐述。
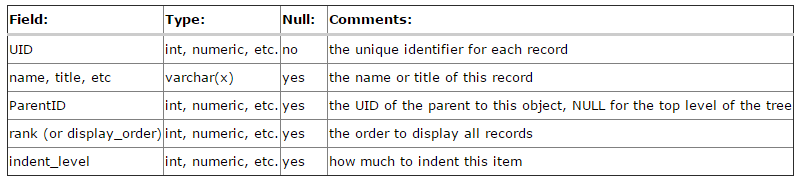
物化路径PathEnumeration
物化路径其实更加容易理解，其实就是在创建节点时，将节点的完整路径进行记录。以下图为例：
按照PathEnumeration进行存储后的结果如下：
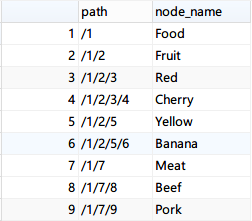
此种方案借助了unix文件目录的思想，主要时以空间换时间。
查询某一节点下的所有子节点:（以Fruit为例）
SET @path=(SELECT path FROM pathTree WHERE node_name='Fruit'); SELECT * FROM pathTree WHERE path like CONCAT(@path, '/%');
如何查询直属子节点？需要采用MySQL的正则表达式查询：
SET @path=(SELECT path FROM pathTree WHERE node_name='Fruit'); SELECT * FROM pathTree WHERE path REGEXP CONCAT(@path, '/', '[0-9]$');
查询任意节点的所有上级：（以Yellow为例）：
SET @path=(SELECT path FROM pathTree WHERE node_name='Yellow'); SELECT * FROM pathTree WHERE @path LIKE CONCAT(path, '%') AND path <> @path;
插入新增数据：
SET @parent_path = (SELECT path FROM pathTree WHERE node_name = 'Fruit'); INSERT INTO pathTree(path, node_name) VALUES(CONCAT(@parent_path, '/', LAST_INSERT_ID() + 1), 'White')
此方案的缺点是树的层级太深有可能会超过PATH字段的长度，所以其能支持的最大深度并非无限的。
如果层级数量是确定的，可以再将所有的列都展开，如下图，比较试用于类似行政区划、生物分类法（界、门、纲、目、科、属、种）这些层级确定的内容。
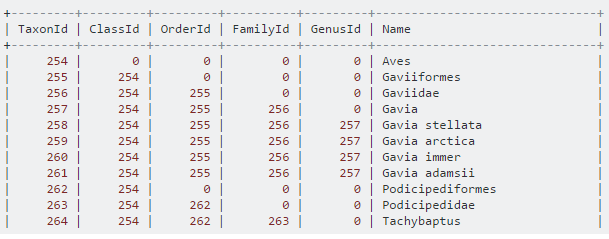
闭包表ClosureTable
将ClosureTable翻译成闭包表不知道是否合适，闭包表的思路和物化路径差不多，都是空间换时间，ClosureTable，一种更为彻底的全路径结构，分别记录路径上相关结点的全展开形式。能明晰任意两结点关系而无须多余查询，级联删除和结点移动也很方便。但是它的存储开销会大一些，除了表示结点的Meta信息，还需要一张专用的关系表。
以下图举例数据举例：
创建主表：
CREATE TABLE nodeInfo( node_id INT NOT NULL AUTO_INCREMENT, node_name VARCHAR(255), PRIMARY KEY(`node_id`) ) DEFAULT CHARSET=utf8;
创建关系表：
CREATE TABLE nodeRelationship( ancestor INT NOT NULL, descendant INT NOT NULL, distance INT NOT NULL, PRIMARY KEY(ancestor, descendant) ) DEFAULT CHARSET=utf8;
其中
- Ancestor代表祖先节点
- Descendant代表后代节点
- Distance祖先距离后代的距离
添加数据（创建存储过程）
CREATE DEFINER=`root`@`localhost` PROCEDURE `AddNode`(`_parent_name` varchar(255), `_node_name` varchar(255)) BEGIN DECLARE _ancestor INT; DECLARE _descendant INT; DECLARE _parent INT; IF NOT EXISTS(SELECT node_id From nodeinfo WHERE node_name = _node_name) THEN INSERT INTO nodeinfo(node_name) VALUES(_node_name); SET _descendant = (SELECT node_id FROM nodeinfo WHERE node_name = _node_name); INSERT INTO noderelationship(ancestor, descendant, distance) VALUES(_descendant, _descendant, 0); IF EXISTS(SELECT node_id FROM nodeinfo WHERE node_name = _parent_name) THEN SET _parent = (SELECT node_id FROM nodeinfo WHERE node_name = _parent_name); INSERT INTO noderelationship(ancestor, descendant, distance) SELECT ancestor, _descendant, distance+1 from noderelationship where descendant = _parent; END IF; END IF; END;
完成后2张表的数据大致是这样的：（注意：每个节点都有一条到其本身的记录。）
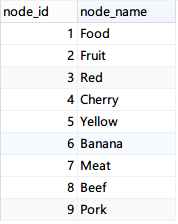
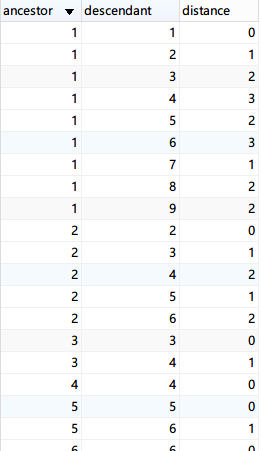
查询Fruit下所有的子节点：
SELECT n3.node_name FROM nodeinfo n1 INNER JOIN noderelationship n2 ON n1.node_id = n2.ancestor INNER JOIN nodeinfo n3 ON n2.descendant = n3.node_id WHERE n1.node_name = 'Fruit' AND n2.distance != 0
查询Fruit下直属子节点：
SELECT n3.node_name FROM nodeinfo n1 INNER JOIN noderelationship n2 ON n1.node_id = n2.ancestor INNER JOIN nodeinfo n3 ON n2.descendant = n3.node_id WHERE n1.node_name = 'Fruit' AND n2.distance = 1
查询Fruit所处的层级：
SELECT n2.*, n3.node_name FROM nodeinfo n1 INNER JOIN noderelationship n2 ON n1.node_id = n2.descendant INNER JOIN nodeinfo n3 ON n2.ancestor = n3.node_id WHERE n1.node_name = 'Fruit' ORDER BY n2.distance DESC
另外要删除节点也非常的简单，这里就不再做过多的阐述。
左右值编码NestedSet
在基于数据库的一般应用中，查询的需求总要大于删除和修改。为了避免对于树形结构查询时的”递归”过程，基于Tree的前序遍历设计一种全新的无递归查询、无限分组的左右值编码方案，来保存该树的数据。
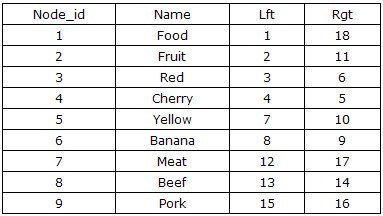
第一次看见这种表结构，相信大部分人都不清楚左值（Lft）和右值（Rgt）是如何计算出来的，而且这种表设计似乎并没有保存父子节点的继承关系。但当你用手指指着表中的数字从1数到18，你应该会发现点什么吧。对，你手指移动的顺序就是对这棵树进行前序遍历的顺序，如下图所示。当我们从根节点Food左侧开始，标记为1，并沿前序遍历的方向，依次在遍历的路径上标注数字，最后我们回到了根节点Food，并在右边写上了18。
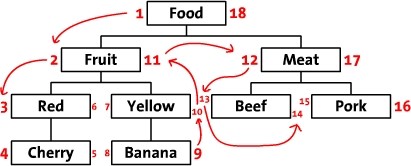依据此设计，我们可以推断出所有左值大于2，并且右值小于11的节点都是Fruit的后续节点，整棵树的结构通过左值和右值存储了下来。然而，这还不够，我们的目的是能够对树进行CRUD操作，即需要构造出与之配套的相关算法。按照深度优先，由左到右的原则遍历整个树，从1开始给每个节点标注上left值和right值，并将这两个值存入对应的name之中。
如何查询？
1、获取某个节点下的所有子孙节点，以Fruit为例：
SELECT * FROM Tree WHERE Lft > 2 AND Lft< 11 ORDER BY Lft ASC
2、获取子孙节点总数
子孙总数=(右值–左值–1)/2，以Fruit为例，其子孙总数为：(11–2–1)/2=4
3、获取节点在树中所处的层数，以Fruit为例：
SELECT COUNT(*) FROM Tree WHERE Lft<= 2 AND Rgt >= 11
4、获取当前节点所在路径，以Fruit为例：
SELECT * FROM Tree WHERE Lft<= 2 AND Rgt >= 11 ORDER BY Lft ASC
在日常的处理中我们经常还会遇到的需要获取某一个节点的直属上级、同级、直属下级。为了更好的描述层级关系，我们可以为Tree建立一个视图，添加一个层次列，该列数值可以编写一个自定义函数来计算：
CREATE FUNCTION `CountLayer`(`_node_id` int) RETURNS int(11) BEGIN DECLARE _result INT; DECLARE _lft INT; DECLARE _rgt INT; IF EXISTS(SELECT Node_id FROM Tree WHERE Node_id = _node_id) THEN SELECT Lft, Rgt FROM Tree WHERE Node_id = _node_id INTO _lft, _rgt; SET _result = (SELECT COUNT(1) FROM Tree WHERE Lft<= _lft AND Rgt >= _rgt); RETURN _result; ELSE RETURN 0; END IF; END;
在添加完函数以后，我们创建一个a视图，添加新的层次列：
CREATE VIEW `NewView` AS SELECT Node_id, Name, Lft, Rgt, CountLayer(Node_id) AS Layer FROM Tree ORDER BY Lft;
5、获取当前节点父节点,以Fruit为例：
SELECT * FROM treeview WHERE Lft<= 2 AND Rgt >= 11 AND Layer = 1
6、获取所有直属子节点，以Fruit为例：
SELECT * FROM treeview WHERE Lft BETWEEN 2 AND 11 AND Layer = 3
7、获取所有兄弟节点，以Fruit为例：
SELECT * FROM treeview WHERE Rgt > 11 AND Rgt< (SELECT Rgt FROM treeview WHERE Lft<= 2 AND Rgt >= 11 AND Layer = 1) AND Layer = 2
8、返回所有叶子节点
SELECT * FROM Tree WHERE Rgt = Lft + 1
如何创建树？如何新增数据？
上面已经介绍了如何检索结果，那么如何才能增加新的节点呢？Nestedset最重要是一定要有一个根节点作为所有节点的起点，而且通常这个节点是不被使用的。为了便于控制查询级别，在建表的时候建议添加parent_id配合之联结列表方式一起使用。
CREATE TABLE IF NOT EXISTS `Tree`( `node_id` int(11) NOT NULL AUTO_INCREMENT, `parent_id` int(10) UNSIGNED NOT NULL DEFAULT '0', `name` varchar(255) NOT NULL, `lft` int(11) NOT NULL DEFAULT '0', `rgt` int(11) NOT NULL DEFAULT '0', PRIMARY KEY (`node_id`), KEY `idx_left_right` (`lft`, `rgt`) ) DEFAULT CHARSET=utf8;
INSERT INTO `Tree`(parent_id, name, lft, rgt) VALUES (0, 'Food', 1, 2)
添加子节点（子节点起始处），以在Food下添加子节点Fruit为例：
LOCK TABLE Tree WRITE; SELECT @parent_id := node_id, @myLeft := lft FROM Tree WHERE name = 'Food'; UPDATE Tree SET rgt = rgt + 2 WHERE rgt > @myLeft; UPDATE Tree SET lft = lft + 2 WHERE lft > @myLeft; INSERT INTO Tree(parent_id, name, lft, rgt) VALUES(@parent_id, 'Fruit', @myLeft + 1, @myLeft + 2); UNLOCK TABLES;
如需在末尾追加就需要以下方式进行（以在Red下添加Apple为例）：
LOCK TABLE Tree WRITE; SELECT @parent_id := node_id, @myRight := rgt FROM Tree WHERE name = 'Red'; UPDATE Tree SET rgt = rgt + 2 WHERE rgt >= @myRight; UPDATE Tree SET lft = lft + 2 WHERE lft > @myRight; INSERT INTO Tree(parent_id, name, lft, rgt) VALUES(@parent_id, 'Apple', @myRight, @myRight + 1); UNLOCK TABLES;
在节点A后面添加同级节点（以在Yellow后面添加Green为例）
LOCK TABLE Tree WRITE; SELECT @parent_id := parent_id, @myRight := rgt FROM Tree WHERE name = 'Yellow'; UPDATE Tree SET rgt = rgt + 2 WHERE rgt > @myRight; UPDATE Tree SET lft = lft + 2 WHERE lft > @myRight; INSERT INTO Tree(parent_id, name, lft, rgt) VALUES(@parent_id, 'Green', @myRight + 1, @myRight + 2); UNLOCK TABLES;
以上讨论的添加节点指的都是添加末端节点，即插入的这个节点不是当前已存在节点的父节点。如果需要插入非末端节点要怎么办呢？
这个过程可以将流程分为2步，首先新增节点，接下里再将需要的节点移到新增的节点下级。节点移动方法(以将Apple移到Yellow中为例)：
LOCK TABLE Tree WRITE; SELECT @nodeId:=node_id, @myLeft:=lft, @myRight:=rgt FROM Tree WHERE name='Apple'; UPDATE Tree SET lft=lft-(@myRight-@myLeft)-1 WHERE lft>@myRight; UPDATE Tree SET rgt=rgt-(@myRight-@myLeft)-1 WHERE rgt>@myRight; SELECT @parent_id:=node_id, @Left:=lft, @Right:=rgt FROM Tree WHERE name='Yellow'; UPDATE Tree SET lft=lft+(@myRight-@myLeft)+1 WHERE lft>@Left; UPDATE Tree SET rgt=rgt+(@myRight-@myLeft)+1 WHERE lft>@Left; UPDATE Tree SET parent_id=@parent_id WHERE name=node_id=@nodeId; UPDATE Tree SET lft=@Left+lft-@myLeft+1, rgt=@Left+lft-@myLeft+1+(@myRight-@myLeft) WHERE lft>=@myLeft AND rgt<=@myRight; UNLOCK TABLES;
删除节点（包含子节点）
LOCK TABLE Tree WRITE; SELECT @myLeft:=lft, @myRight:=rgt FROM Tree WHERE name='Apple'; DELETE Tree WHERE lft>=@myLeft AND rgt<=@myRight; UPDATE Tree SET lft=lft-(@myRight-@myLeft)-1 WHERE lft>@myRight; UPDATE Tree SET rgt=rgt-(@myRight-@myLeft)-1 WHERE rgt>@myRight; UNLOCK TABLES;
如果需要只删除该节点，子节点自动上移一级如何处理？
LOCK TABLE Tree WRITE; SELECT @parent_id:=parent_id, @node_id:=node_id, @myLeft:=lft, @myRight:=rgt FROM Tree WHERE name='Red'; UPDATE Tree SET parent_id=@parent_id WHERE parent_id=@node_id DELETE Tree WHERE lft=@myLeft; UPDATE Tree SET lft=lft-1, rgt=rgt-1 Where lft>@myLeft AND @rgt<@myRight UPDATE Tree SET lft=lft-2, rgt=rgt-2 Where lft>@rgt>@myRight UNLOCK TABLES;
以上为NestedSet的CURD操作，具体在使用时建议结合事务和存储过程一起使用。本方案的优点时查询非常的方便，缺点就是每次插入删除数据涉及到的更新内容太多，如果树非常大，插入一条数据可能花很长的时间。
区间嵌套NestedIntervals
前面介绍了左右值编码，不知道大家注意到了没有，如果数据庞大，每次更新都需要更新差不多全表，效率较低没有更好的方式？今天我们就来研究下区间嵌套法。
区间嵌套法原理
如果节点区间[clft,crgt]与[plft,prgt]存在如下关系：plft<=clft and crgt>=prgt，则[clft,crgt]区间里的点是[plft,prgt]的子节点。基于此假设我们就可以通过对区间的不断的向下划来获取新的区间。举例：如果在区间[plft,prgt]中存在一个空白区间[lft1,rgt1]，如果要加入一个[plft,lft1]、[rgt1,prgt]同级的区间，只需插入节点：[(2*lft1+rgt1)/3, (rgt1+2*lft)/3]。在添加完节点后我们还留下[lft1,(2*lft1+rgt1)/3]和[(rgt1+2*lft)/3,rgt1]两个空余的空间用来添加更多的子节点。
如果我们把区间放在二位平面上，把rgt当成是x轴，lft当做是y轴，那么嵌套的区间数差不多是这样的：
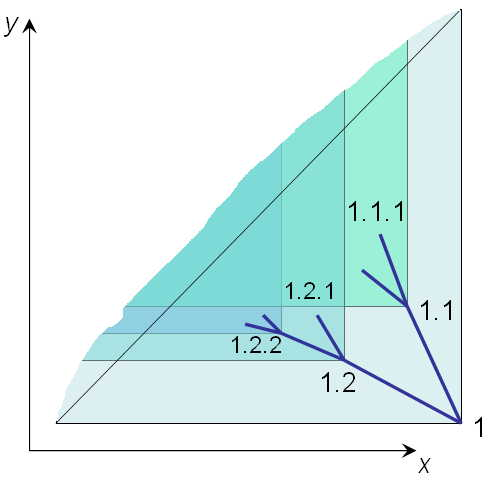
每个节点[lft,rgt]拥有的子节点都被包含在y>=lft & x<=rgt中。同时y>=clft & x<=crgt所在的空间也是y>=plft & x<=prgt的子集。另外由于新增的右区间都小于已有的左区间，所以新增的节点均在y=x这条直线以下。 区间嵌套法实现
了解了区间嵌套法的原理后，接下来我们就要考虑如何实现他，原则上初始的区间使用任何区间都是可以的，这里我们使用的是[0,1]作为根区间。
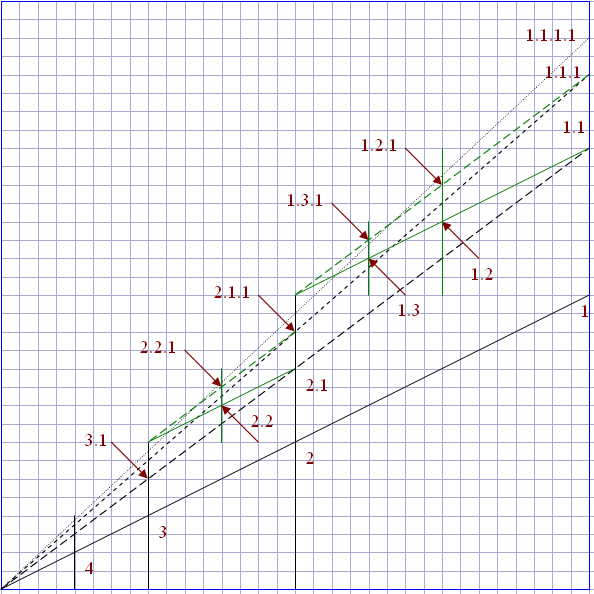
首先，我们在XY平面上定义2个点。深度优先集合点和广度有限集合点，针对点
另外仔细看我们可以看到点与点之间的关系。另外如果我们知道x和y的和，我们就能反推出x,y的值（具体的逻辑是什么，我现在也还没有搞懂，有知道的朋友可以帮忙解释下）。
我们以节点
我们定义11为分子（numerator），8为分母（denominator），则x点的分子为：
CREATE DEFINER=`root`@`localhost` FUNCTION `x_numer`(`numer` int, `denom` int) RETURNS int(11) BEGIN DECLARE ret_num INT; DECLARE ret_den INT; SET ret_num:=numer+1; SET ret_den:=denom*2; WHILE floor(ret_num/2)=ret_num/2 DO SET ret_num:=ret_num/2; SET ret_den:=ret_den/2; END WHILE; RETURN ret_num; END;
x点的分母为：
CREATE DEFINER=`root`@`localhost` FUNCTION `x_denom`(`numer` int, `denom` int) RETURNS int(11) BEGIN DECLARE ret_num INT; DECLARE ret_den INT; SET ret_num:=numer+1; SET ret_den:=denom*2; WHILE floor(ret_num/2)=ret_num/2 DO SET ret_num:=ret_num/2; SET ret_den:=ret_den/2; END WHILE; RETURN ret_den; END;
Y点的分子：CREATE DEFINER=`root`@`localhost` FUNCTION `y_numer`(`numer` int, `denom` int)
RETURNS int(11)
BEGIN
DECLARE num INT;
DECLARE den INT;
SET num := x_numer(numer, denom);
SET den := x_denom(numer, denom);
WHILE den< denom DO
SET num := num * 2;
SET den := den * 2;
END WHILE;
SET num := (numer - num);
WHILE floor(num / 2) = num / 2 DO
SET num := num / 2;
SET den := den / 2;
END WHILE;
RETURN num;
END;
Y的分母：
CREATE DEFINER=`root`@`localhost` FUNCTION `y_denom`(`numer` int, `denom` int) RETURNS int(11) BEGIN DECLARE num INT; DECLARE den INT; SET num := x_numer(numer, denom); SET den := x_denom(numer, denom); WHILE den< denom DO SET num := num * 2; SET den := den * 2; END WHILE; SET num := (numer - num); WHILE floor(num / 2) = num / 2 DO SET num := num / 2; SET den := den / 2; END WHILE; RETURN den; END;
接下来我们来测试下，X与Y是否能解码出来：
SELECT CONCAT(x_numer(11, 8), '/', x_denom(11, 8)) AS X, CONCAT(y_numer(11, 8), '/', y_denom(11, 8)) AS Y
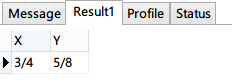
结果与节点1.2的位置为<x=3/4, y=5/8>完全一致。现在我们知道只需要一个分数即可表示平面上的一个点。
如有已经有分数11/8如何获取该节点的父节点？(如果分子为3，则代表其为根节点)
CREATE DEFINER=`root`@`localhost` FUNCTION `parent_numer`(`numer` int, `denom` int) RETURNS int(11) BEGIN DECLARE ret_num INT; DECLARE ret_den INT; IF numer = 3 THEN RETURN denom / 2; END IF; SET ret_num := (numer - 1) / 2; SET ret_den := denom / 2; WHILE floor((ret_num - 1) / 4) = (ret_num - 1) / 4 DO SET ret_num := (ret_num + 1) / 2; SET ret_den := ret_den / 2; END WHILE; RETURN ret_num; END;
SELECT CONCAT(parent_numer(11, 8), '/', parent_denom(11, 8)) AS parent
计算当前节点在同级所在的位置：
CREATE DEFINER=`root`@`localhost` FUNCTION `parent_denom`(`numer` int, `denom` int) RETURNS int(11) BEGIN DECLARE ret_num INT; DECLARE ret_den INT; IF numer = 3 THEN RETURN NULL; END IF; SET ret_num := (numer - 1) / 2; SET ret_den := denom / 2; WHILE floor((ret_num - 1) / 4) = (ret_num - 1) / 4 DO SET ret_num := (ret_num + 1) / 2; SET ret_den := ret_den / 2; END WHILE; RETURN ret_den; END;
有了查询父节点的方法及当前节点所在同级中的位置的方法，即可通过这两个的组合，将节点的路径给计算出来。
CREATE DEFINER=`root`@`localhost` FUNCTION `path`(`numer` int, `denom` int) RETURNS varchar(255) BEGIN IF numer is NULL THEN RETURN ''; END IF; RETURN path(parent_numer(numer, denom), parent_denom(numer, denom)) || ‘.’ || sibling_number(numer, denom); END;
按照以上方法添加后进行测试，返回[Err] 1424 - Recursive stored functions and triggers are not allowed.即MySQL的自定义函数不支持递归查询。
CREATE DEFINER=`root`@`localhost` FUNCTION `path`(`numer` int, `denom` int) RETURNS varchar(255) BEGIN DECLARE numer_temp INT; DECLARE denom_temp INT; DECLARE path_result VARCHAR(255); DECLARE path_temp VARCHAR(255); DECLARE sn VARCHAR(255); SET path_temp := ''; WHILE numer IS NOT NULL DO IF path_temp = '' THEN SET path_result := sibling_number(numer, denom); ELSE SET path_result := CONCAT(sibling_number(numer, denom), '.', path_temp); END IF; SET path_temp := path_result; SET numer_temp := parent_numer(numer, denom); SET denom_temp := parent_denom(numer, denom); SET numer := numer_temp; SET denom := denom_temp; END WHILE; RETURN path_result; END;
SELECT path(11, 8)的结果为1.2
计算节点层级的方法：
CREATE DEFINER=`root`@`localhost` FUNCTION `node_level`(`numer` int, `denom` int) RETURNS int(11) BEGIN DECLARE ret_num INT; DECLARE ret_den INT; DECLARE ret INT; SET ret = 1; IF numer = 3 THEN return 1; END IF; WHILE numer != 3 DO SET ret_num := parent_numer(numer, denom); SET ret_den := parent_denom(numer, denom); SET numer := ret_num; SET denom := ret_den; SET ret := ret + 1; END WHILE; RETURN ret; END;
我们知道了如何将编码过的节点转成目录形式，如何逆转呢？以下是方法：
先添加2个辅助函数：
CREATE DEFINER=`root`@`localhost` FUNCTION `child_numer`(`num` int, `den` int, `child` int) RETURNS int(11) BEGIN RETURN num * power(2, child) + 3 - power(2, child); END;CREATE DEFINER=`root`@`localhost` FUNCTION `child_denom`(`num` int, `den` int, `child` int) RETURNS int(11) BEGIN RETURN den * power(2, child); END;再来编写逆转函数：
CREATE DEFINER=`root`@`localhost` FUNCTION `path_numer`(`path` varchar(255)) RETURNS int(11) BEGIN DECLARE num INT; DECLARE den INT; DECLARE postfix VARCHAR(255); DECLARE sibling VARCHAR(255); SET num := 1; SET den := 1; SET postfix := CONCAT(path, '.'); WHILE length(postfix) > 1 DO SET sibling := SUBSTR(postfix, 1, instr(postfix, '.') - 1); SET postfix := SUBSTR(postfix, instr(postfix, '.') + 1); SET num := child_numer(num, den, sibling + 0); SET den := child_denom(num, den, sibling + 0); END WHILE; RETURN num; END;CREATE DEFINER=`root`@`localhost` FUNCTION `path_denom`(`path` varchar(255)) RETURNS int(11) BEGIN DECLARE num INT; DECLARE den INT; DECLARE postfix VARCHAR(255); DECLARE sibling VARCHAR(255); SET num := 1; SET den := 1; SET postfix := CONCAT(path, '.'); WHILE length(postfix) > 1 DO SET sibling := SUBSTR(postfix, 1, instr(postfix, '.') - 1); SET postfix := SUBSTR(postfix, instr(postfix, '.') + 1); SET num := child_numer(num, den, sibling + 0); SET den := child_denom(num, den, sibling + 0); END WHILE; RETURN den; END;select CONCAT(path_numer('2.1.3'), '/', path_denom('2.1.3')) 结果为 51/64
参考链接：
