什么是余弦定理
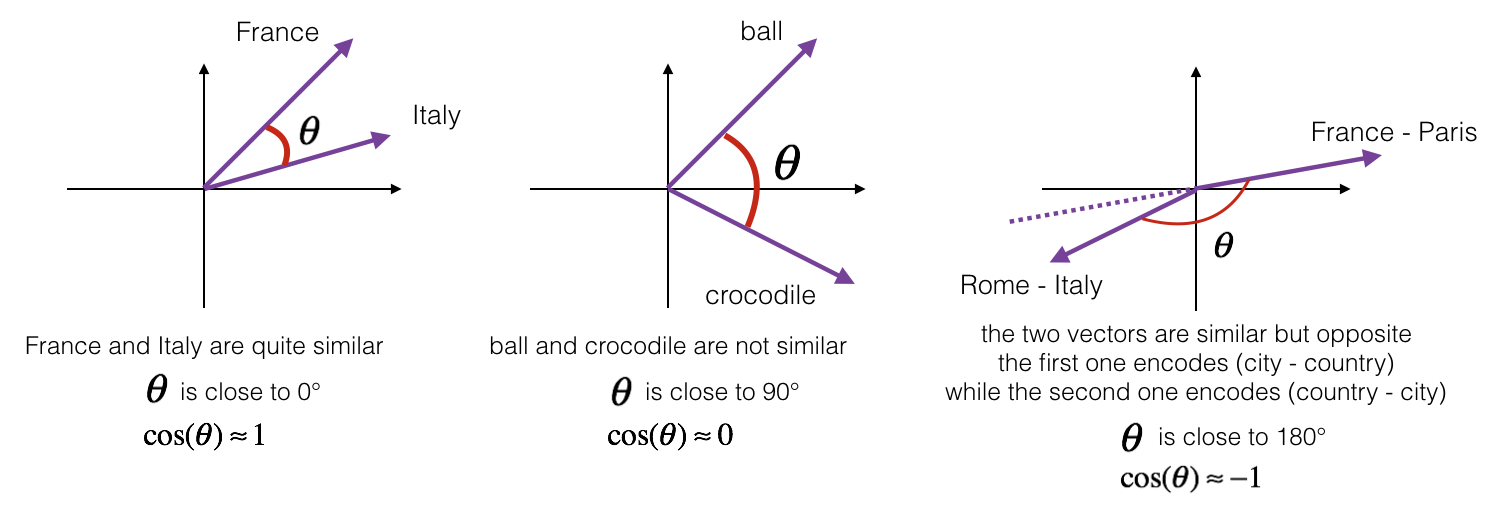
学过向量代数的人都知道,向量实际上是多维空间中有方向的线段。如果两个向量的方向一致,即夹角接近零,那么这两个向量就相近。而要确定两个向量方向是否一致,这就要用到余弦定理计算向量的夹角了。
余弦定理对我们每个人都不陌生,它描述了三角形中任何一个夹角和三个边的关系,换句话说,给定三角形的三条边,我们可以用余弦定理求出三角形各个角的角度。假定三角形的三条边为a,b和c,对应的三个角为A,B和C,那么角A的余弦:
$$\cos{A}=\frac{b^2+c^2-a^2}{2bc}$$
如果我们将三角形的两边b和c看成是两个向量,那么上述公式等价于:
$$\cos{A}=\frac{<b,c>}{|b||c|}$$
其中分母表示两个向量b和c的长度,分子表示两个向量的内积。举一个具体的例子,假如文本X和文本Y对应向量分别是:
- x_1,x_2,…,x_64000
- y_1,y_2,…,y_64000
那么它们夹角的余弦等于:
$$\cos{\theta}=\frac{x_1y_1+x_2y_2+…+x_{64000}y_{64000}}{\sqrt{x_1^2+x_2^2+…+x_{64000}^2}\cdot\sqrt{y_1^2+y_2^2+…+y_{64000}^2}}$$
当两个文本向量夹角的余弦等于1时,这两个文本完全重复;当夹角的余弦接近于一时,两条新闻相似;夹角的余弦越小,两条文本越不相关。
计算文本相似度的大致流程
假设有下面两个句子:
- A:我喜欢看电视,不喜欢看电影。
- B:我不喜欢看电视,也不喜欢看电影。
第一步:分词
- A:我/喜欢/看/电视,不/喜欢/看/电影。
- B:我/不/喜欢/看/电视,也/不/喜欢/看/电影。
第二步:列出所有的词、字
我,喜欢,看,电视,电影,不,也第三步:计算词频
- A:我1,喜欢2,看2,电视1,电影1,不1,也0。
- B:我1,喜欢2,看2,电视1,电影1,不2,也1。
第四步:描述词频向量
- A:[1,2,2,1,1,1,0]
- B:[1,2,2,1,1,2,1]
第五步:计算夹角余弦
使用这个公式,我们就可以得到,句子A与句子B的夹角的余弦。
余弦值越接近1,就表明夹角越接近0度,也就是两个向量越相似,这就叫”余弦相似性”。所以,上面的句子A和句子B是很相似。
实际使用过程需要注意的事项
- 实际使用中文本长度可能过长,如果采用分词,复杂度较高,可以采用TF-IDF的方式找出文章若干个关键词(比如20个),再进行比较。
- 文章的长度可能不一致,所以关键词词频率可以使用相对词频率。
- 由于计算中打乱了关键词出现的顺序,所以即使夹角余弦的值为1,也有可能文本并不重复。比如:
- A:我喜欢看电视,不喜欢看电影。
- B:我不喜欢看电视,喜欢看电影。
使用Python进行文本相似度计算
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from __future__ import division
import jieba.analyse
from math import sqrt
class Similarity():
def __init__(self, target1, target2, topK=10):
self.target1 = target1
self.target2 = target2
self.topK = topK
def vector(self):
self.vdict1 = {}
self.vdict2 = {}
top_keywords1 = jieba.analyse.extract_tags(self.target1, topK=self.topK, withWeight=True)
top_keywords2 = jieba.analyse.extract_tags(self.target2, topK=self.topK, withWeight=True)
for k, v in top_keywords1:
self.vdict1[k] = v
for k, v in top_keywords2:
self.vdict2[k] = v
def mix(self):
for key in self.vdict1:
self.vdict2[key] = self.vdict2.get(key, 0)
for key in self.vdict2:
self.vdict1[key] = self.vdict1.get(key, 0)
def mapminmax(vdict):
"""计算相对词频"""
_min = min(vdict.values())
_max = max(vdict.values())
_mid = _max - _min
#print _min, _max, _mid
for key in vdict:
vdict[key] = (vdict[key] - _min)/_mid
return vdict
self.vdict1 = mapminmax(self.vdict1)
self.vdict2 = mapminmax(self.vdict2)
def similar(self):
self.vector()
self.mix()
sum = 0
for key in self.vdict1:
sum += self.vdict1[key] * self.vdict2[key]
A = sqrt(reduce(lambda x, y: x + y, map(lambda x: x * x, self.vdict1.values())))
B = sqrt(reduce(lambda x, y: x + y, map(lambda x: x * x, self.vdict2.values())))
return sum/(A * B)
if __name__ == '__main__':
t1 = '''余弦定理和新闻的分类似乎是两件八杆子打不着的事,但是它们确有紧密的联系。具体说,新闻的分类很大程度上依靠余弦定理。Google的新闻是自动分类和整理的。所谓新闻的分类无非是要把相似的新闻放到一类中。计算机其实读不懂新闻,它只能快速计算。这就要求我们设计一个算法来算出任意两篇新闻的相似性。为了做到这一点,我们需要想办法用一组数字来描述一篇新闻。我们来看看怎样找一组数字,或者说一个向量来描述一篇新闻。回忆一下我们在“如何度量网页相关性”一文中介绍的TF/IDF的概念。对于一篇新闻中的所有实词,我们可以计算出它们的单文本词汇频率/逆文本频率值(TF/IDF)。不难想象,和新闻主题有关的那些实词频率高,TF/IDF值很大。我们按照这些实词在词汇表的位置对它们的TF/IDF值排序。比如,词汇表有六万四千个词,分别为'''
t2 = '''新闻分类——“计算机的本质上只能做快速运算,为了让计算机能够“算”新闻”(而不是读新闻),就要求我们先把文字的新闻变成一组可计算的数字,然后再设计一个算法来算出任何两篇新闻的相似性。“——具体做法就是算出新闻中每个词的TF-IDF值,然后按照词汇表排成一个向量,我们就可以对这个向量进行运算了,那么如何度量两个向量?——向量的夹角越小,那么我们就认为它们更相似,而长度因为字数的不同并没有太大的意义。——如何计算夹角,那就用到了余弦定理(公式略)。——如何建立新闻类别的特征向量,有两种方法,手工和自动生成。至于自动分类的方法,书本上有介绍,我这里就略过了。很巧妙,但是我的篇幅肯定是放不下的。除余弦定理之外,还可以用矩阵的方法对文本进行分类,但这种方法需要迭代很多次,对每个新闻都要两两计算,但是在数学上有一个十分巧妙的方法——奇异值分解(SVD)。奇异值分解,就是把上面这样的大矩阵,分解为三个小矩阵的相乘。这三个小矩阵都有其物理含义。这种方法能够快速处理超大规模的文本分类,但是结果略显粗陋,如果两种方法一前一后结合使用,既能节省时间,又提高了精确性。'''
topK = 10
s = Similarity(t1, t2, topK)
print s.similar()
参考文章:



