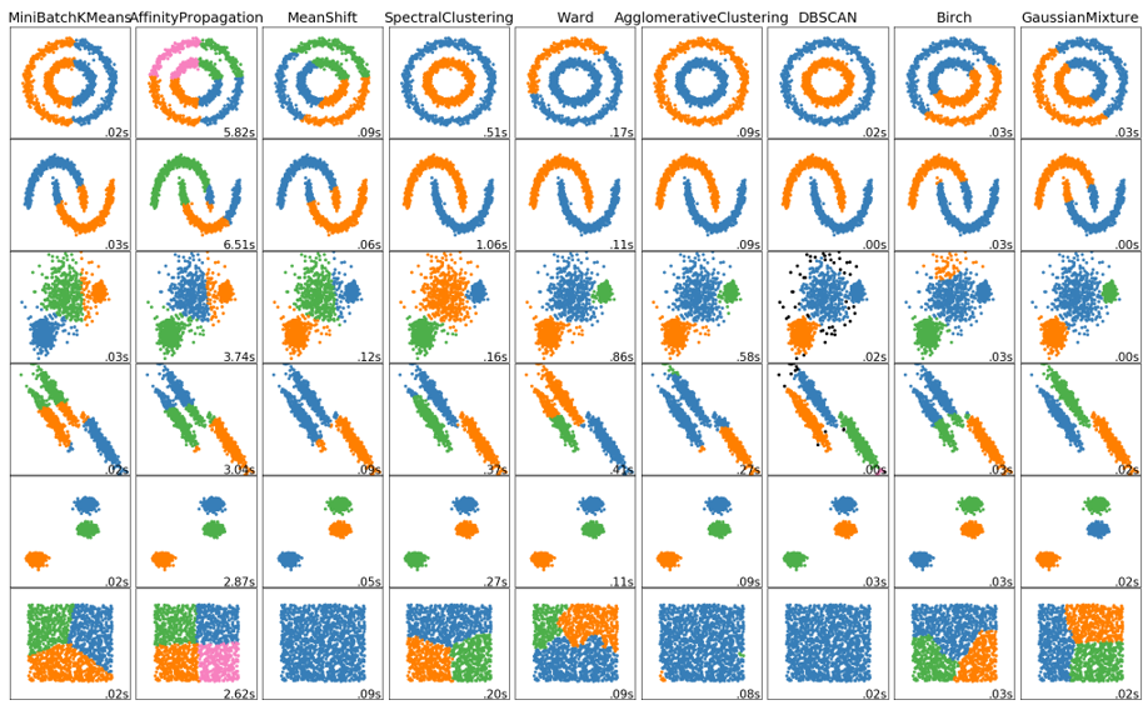
在学习聚类算法得时候并没有涉及到评估指标,主要原因是聚类算法属于非监督学习,并不像分类算法那样可以使用训练集或测试集中得数据计算准确率、召回率等。那么如何评估聚类算法得好坏呢?好的聚类算法,一般要求类簇具有:
- 高的类内 (intra-cluster) 相似度
- 低的类间 (inter-cluster) 相似度
对于聚类算法大致可分为 2类度量标准:
- 内部评估的方法:通过一个单一的量化得分来评估算法好坏;该类型的方法
- 外部评估的方法:通过将聚类结果与已经有“ground truth”分类进行对比。要么通过人类进行手动评估,要么通过一些指标在特定的应用场景中进行聚类用法的评估。不过该方法是有问题的,如果真的有了label,那么还需要聚类干嘛,而且实际应用中,往往都没label;另一方面,这些label只反映了数据集的一个可能的划分方法,它并不能告诉你存在一个不同的更好的聚类算法。
内部评价指标
当一个聚类结果是基于数据聚类自身进行评估的,这一类叫做内部评估方法。如果某个聚类算法聚类的结果是类间相似性低,类内相似性高,那么内部评估方法会给予较高的分数评价。不过内部评价方法的缺点是:
- 那些高分的算法不一定可以适用于高效的信息检索应用场景;
- 这些评估方法对某些算法有倾向性,如k-means聚类都是基于点之间的距离进行优化的,而那些基于距离的内部评估方法就会过度的赞誉这些生成的聚类结果。
这些内部评估方法可以基于特定场景判定一个算法要优于另一个,不过这并不表示前一个算法得到的结果比后一个结果更有意义。这里的意义是假设这种结构事实上存在于数据集中的,如果一个数据集包含了完全不同的数据结构,或者采用的评价方法完全和算法不搭,比如k-means只能用于凸集数据集上,许多评估指标也是预先假设凸集数据集。在一个非凸数据集上不论是使用k-means还是使用假设凸集的评价方法,都是徒劳的。
SSE(和方差)
该统计参数计算的是拟合数据和原始数据对应点的误差的平方和,计算公式如下:
$$\sum_{i=1}^{n}{(y_i – \hat{y_i})^2}$$
SSE越接近于0,说明模型选择和拟合更好,数据预测也越成功。
#断崖图选取最优K值
import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# '利用SSE选择k'
SSE = [] # 存放每次结果的误差平方和
for k in range(1,9):
estimator = KMeans(n_clusters=k) # 构造聚类器
estimator.fit(df[['calories','sodium','alcohol','cost']])
SSE.append(estimator.inertia_)
N = range(1,9)
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(N,SSE,'o-')
plt.show()
轮廓系数 Silhouette Coefficient
轮廓系数适用于实际类别信息未知的情况。对于单个样本,设a是与它同类别中其他样本的平均距离,b是与它距离最近不同类别中样本的平均距离,其轮廓系数为:
$$s = \frac{b-a}{\max(a,b)}$$
对于一个样本集合,它的轮廓系数是所有样本轮廓系数的平均值。轮廓系数的取值范围是[-1,1],同类别样本距离越相近不同类别样本距离越远,分数越高。缺点:不适合基高密度的聚类算法DBSCAN。
from sklearn import metrics from sklearn.metrics import pairwise_distances from sklearn import datasets dataset = datasets.load_iris() X = dataset.data y = dataset.target import numpy as np from sklearn.cluster import KMeans kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X) labels = kmeans_model.labels_ metrics.silhouette_score(X, labels, metric='euclidean')
Calinski-Harabaz Index
在真实的分群label不知道的情况下,Calinski-Harabasz可以作为评估模型的一个指标。Calinski-Harabasz指标通过计算类中各点与类中心的距离平方和来度量类内的紧密度,通过计算各类中心点与数据集中心点距离平方和来度量数据集的分离度,CH指标由分离度与紧密度的比值得到。从而,CH越大代表着类自身越紧密,类与类之间越分散,即更优的聚类结果。
$$s(k)=\frac{tr(B_k)}{tr(W_k)}\frac{m-k}{k-1}$$
其中m为训练样本数,k是类别个数,$B_k$是类别之间协方差矩阵,$W_k$是类别内部数据协方差矩阵,$tr$为矩阵的迹。也就是说,类别内部数据的协方差越小越好,类别之间的协方差越大越好,这样的Calinski-Harabasz分数会高。同时,数值越小可以理解为:组间协方差很小,组与组之间界限不明显。
优点
- 当 cluster (簇)密集且分离较好时,分数更高,这与一个标准的 cluster(簇)有关。
- 得分计算很快与轮廓系数的对比,最大的优势:快!相差几百倍!毫秒级。
缺点
- 凸的簇的 Calinski-Harabaz index(Calinski-Harabaz 指数)通常高于其他类型的 cluster(簇),例如通过 DBSCAN 获得的基于密度的 cluster(簇)。所以不适合基于密度的聚类算法,DBSCAN。
import numpy as np from sklearn.cluster import KMeans kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X) labels = kmeans_model.labels_ print(metrics.calinski_harabaz_score(X, labels))
Compactness(紧密性)(CP)
CP计算每一个类各点到聚类中心的平均距离CP越低意味着类内聚类距离越近。著名的 K-Means 聚类算法就是基于此思想提出的。缺点:没有考虑类间效果。
$$\overline{CP}_i = \frac{1}{n_i} \sum_{x\in C_i} \mid\mid x_i – \mu_i \mid\mid$$
$$\overline{CP} =\frac{1}{k} \sum_{k=1}^k \overline{CP}_k$$
Separation(间隔性)(SP)
SP计算各聚类中心两两之间平均距离,SP越高意味类间聚类距离越远。缺点:没有考虑类内效果。
$$\overline{SP} = \frac{2}{k_2 – k} \sum_{i=1}^k \sum_{j=i+1}^k \mid\mid \mu_i – \mu_j \mid\mid$$
Davies-Bouldin Index(戴维森堡丁指数)(分类适确性指标)(DB)(DBI)
DB计算任意两类别的类内距离平均距离(CP)之和除以两聚类中心距离求最大值。DB越小意味着类内距离越小同时类间距离越大。该指标的计算公式:
$$\text{DB}=\frac{1}{n} \sum_{i=1}^{n} \max _{j \neq i}(\frac{\sigma_{i}+\sigma_{j}}{d(c_{i}, c_{j})})$$
其中n是类别个数,$c_i$是第i个类别的中心,$\sigma_{i}$是类别i中所有的点到中心的平均距离;$d(c_{i}, c_{j})$中心点$c_{i}$和$c_{j}$之间的距离。算法生成的聚类结果越是朝着类内距离最小(类内相似性最大)和类间距离最大(类间相似性最小)变化,那么Davies-Bouldin指数就会越小。缺点:因使用欧式距离所以对于环状分布聚类评测很差。
from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn.metrics import davies_bouldin_score
from sklearn.datasets.samples_generator import make_blobs
# loading the dataset
X, y_true = make_blobs(n_samples=300, centers=4,
cluster_std=0.50, random_state=0)
# K-Means
kmeans = KMeans(n_clusters=4, random_state=1).fit(X)
# we store the cluster labels
labels = kmeans.labels_
print(davies_bouldin_score(X, labels))
Dunn Validity Index (邓恩指数)(DVI)
DVI计算任意两个簇元素的最短距离(类间)除以任意簇中的最大距离(类内)。DVI越大意味着类间距离越大同时类内距离越小。
$$D=\frac{\min _{1 \leq i<j \leq n} d(i, j)}{\max _{1 \leq k \leq n} d^{\prime}(k)}$$
其中$d(i,j)$表示类别$i$,$j$之间的距离;$d'(k)$表示类别$k$内部的类内距离:
- 类间距离$d(i,j)$可以是任意的距离测度,例如两个类别的中心点的距离;
- 类内距离$d'(k)$可以以不同的方法去测量,例如类别kk中任意两点之间距离的最大值。
因为内部评估方法是搜寻类内相似最大,类间相似最小,所以算法生成的聚类结果的Dunn指数越高,那么该算法就越好。缺点:对离散点的聚类测评很高、对环状分布测评效果差。
import pandas as pd from sklearn import datasets from jqmcvi import base # loading the dataset X = datasets.load_iris() df = pd.DataFrame(X.data) # K-Means from sklearn import cluster k_means = cluster.KMeans(n_clusters=3) k_means.fit(df) #K-means training y_pred = k_means.predict(df) # We store the K-means results in a dataframe pred = pd.DataFrame(y_pred) pred.columns = ['Type'] # we merge this dataframe with df prediction = pd.concat([df, pred], axis = 1) # We store the clusters clus0 = prediction.loc[prediction.Species == 0] clus1 = prediction.loc[prediction.Species == 1] clus2 = prediction.loc[prediction.Species == 2] cluster_list = [clus0.values, clus1.values, clus2.values] print(base.dunn(cluster_list))
外部评价指标
在外部评估方法中,聚类结果是通过使用没被用来做训练集的数据进行评估。例如已知样本点的类别信息和一些外部的基准。这些基准包含了一些预先分类好的数据,比如由人基于某些场景先生成一些带label的数据,因此这些基准可以看成是金标准。这些评估方法是为了测量聚类结果与提供的基准数据之间的相似性。然而这种方法也被质疑不适用真实数据。
纯度(Purity)
纯度(Purity)是一种简单而透明的评估手段,为了计算纯度(Purity),我们把每个簇中最多的类作为这个簇所代表的类,然后计算正确分配的类的数量,然后除以N。形式化表达如下:
$$\text{purity}(\Omega, \mathbb{C})=\frac{1}{N} \sum_{k} \max _{j} |\omega_{k} \cap c_{j} |$$
其中:
- $\Omega = \{w_1,w_2,…,w_k\}$是聚类的集合,$w_k$表示第k个聚类的集合。
- $\mathbb{C} = \{c_1,c_2,…,c_j\}$是文档集合,$c_j$表示第J个文档。
- $N$表示文档总数。
上述过程即给每个聚类簇分配一个类别,且这个类别的样本在该簇中出现的次数最多,然后计算所有 K 个聚类簇的这个次数之和再归一化即为最终值。Purity值在0~1之间 ,越接近1表示聚类结果越好。
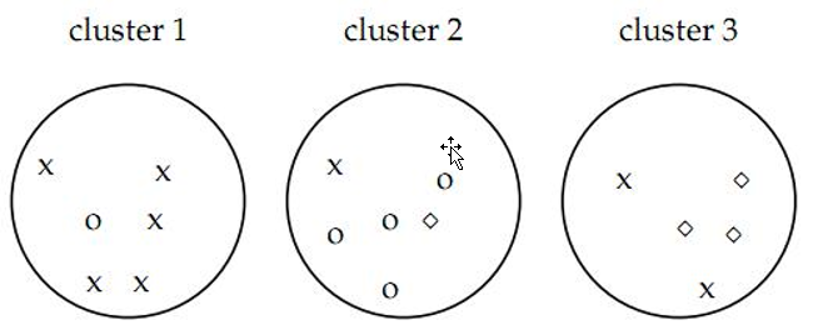
如图认为x代表一类文档,o代表一类文档,方框代表一类文档。如上图的purity = ( 3+ 4 + 5) / 17 = 0.71,其中第一类正确的有5个,第二个4个,第三个3个,总文档数17。
当簇的数量很多的时候,容易达到较高的纯度——特别是,如果每个文档都被分到独立的一个簇中,那么计算得到的纯度就会是1。因此,不能简单用纯度来衡量聚类质量与聚类数量之间的关系。另外Purity无法用于权衡聚类质量与簇个数之间的关系。
def purity(result, label):
# 计算纯度
total_num = len(label)
cluster_counter = collections.Counter(result)
original_counter = collections.Counter(label)
t = []
for k in cluster_counter:
p_k = []
for j in original_counter:
count = 0
for i in range(len(result)):
if result[i] == k and label[i] == j: # 求交集
count += 1
p_k.append(count)
temp_t = max(p_k)
t.append(temp_t)
return sum(t)/total_num
标准化互信息(NMI)
互信息(Normalized Mutual Information)是用来衡量两个数据分布的吻合程度。也是一有用的信息度量,它是指两个事件集合之间的相关性。互信息越大,词条和类别的相关程度也越大。NMI (Normalized Mutual Information) 即归一化互信息:
$$\text{NMI}(\Omega, C)=\frac{I(\Omega ; C)}{(H(\Omega)+H(C) / 2)}$$
其中,$I$表示互信息(Mutual Information), $H$为熵,当 log 取 2 为底时,单位为 bit,取 e 为底时单位为 nat。
$$c =\sum_{k}\sum_{j}P(w_{k} \cap c_{j}) \log \frac{P(w_{k} \cap c_{j})}{P(w_{k}) P(c_{j})} =\sum_{k} \sum_{j} \frac{|w_{k} \cap c_{j}|}{N} \log \frac{N|w_{k} \cap c_{j}|}{|w_{k}t||c_{j}|}$$
其中, $P(w_k),P(c_j),P(w_k\cap c_j)$可以分别看作样本 (document) 属于聚类簇$w_k$, 属于类别$c_j$, 同时属于$w_k, c_j$的概率。第二个等价式子则是由概率的极大似然估计推导而来。
$$H(\Omega )= -\sum_{k}P(w_k)\log P(w_k) = -\sum_{k}\frac{|w_k|}{N}\log\frac{|w_k|}{N}$$
互信息$I(\Omega;C)$表示给定类簇信息$C$的前提条件下,类别信息$\Omega$的增加量,或者说其不确定度的减少量。直观地,互信息还可以写出如下形式:$H(\Omega; C )= H(\Omega)-H(\Omega|C )$
互信息的最小值为 0, 当类簇相对于类别只是随机的, 也就是说两者独立的情况下, $\Omega$对于$C$未带来任何有用的信息.如果得到的$\Omega$与$C$关系越密切, 那么$I(\Omega;C)$值越大。如果$\Omega$完整重现了$C$, 此时互信息最大:$H(\Omega; C )= H(\Omega)=H(C)$
当K=N时,即类簇数和样本个数相等,MI 也能达到最大值。所以 MI 也存在和纯度类似的问题,即它并不对簇数目较大的聚类结果进行惩罚,因此也不能在其他条件一样的情况下,对簇数目越小越好的这种期望进行形式化。NMI 则可以解决上述问题,因为熵会随着簇的数目的增长而增大。当K=N时,$ H(\Omega)$会达到其最大值$\log N$ , 此时就能保证 NMI 的值较低。之所以采用$(H(\Omega)+H(C)/2$作为分母是因为它是 $I(\Omega,C)$的紧上界, 因此可以保证$\text{NMI}\in [0,1]$。
示例:
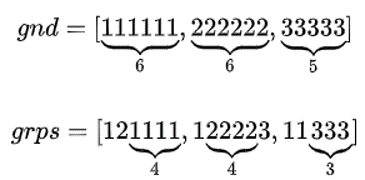
gnd 是 ground truth 的意思,grps 表示聚类后的 groups. 问题:计算序列 gnd 和 grps 的 NMI.
先计算联合概率分布$p(grap,gnd)$
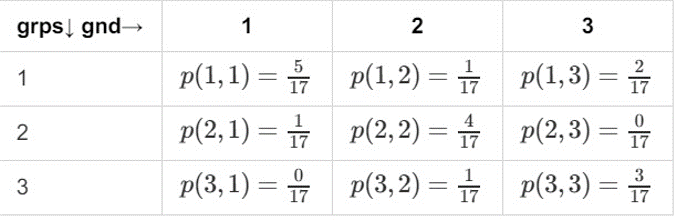
计算边际分布
$$P(gnd)=(\frac{6}{17},\frac{6}{17},\frac{5}{17})$$
$$P(grps)=(\frac{8}{17},\frac{5}{17},\frac{4}{17})$$
计算熵和互信息
$$H(gnd) = 1.58$$
$$H(grps) = 1.522$$
$$H(gnd|grps) = 1.014$$
$$I(gnd;grps) = H(gnd)-H(gnd|grps)=0.564$$
计算 NMI
$$\text{NMI} = \frac{2\times I(gnd;grps)}{H(gnd)+H(grps)} \approx 0.3649$$
代码实现:
def NMI(result, label):
# 标准化互信息
total_num = len(label)
cluster_counter = collections.Counter(result)
original_counter = collections.Counter(label)
# 计算互信息量
MI = 0
eps = 1.4e-45 # 取一个很小的值来避免log 0
for k in cluster_counter:
for j in original_counter:
count = 0
for i in range(len(result)):
if result[i] == k and label[i] == j:
count += 1
p_k = 1.0*cluster_counter[k] / total_num
p_j = 1.0*original_counter[j] / total_num
p_kj = 1.0*count / total_num
MI += p_kj * math.log(p_kj /(p_k * p_j) + eps, 2)
# 标准化互信息量
H_k = 0
for k in cluster_counter:
H_k -= (1.0*cluster_counter[k] / total_num) * math.log(1.0*cluster_counter[k] / total_num+eps, 2)
H_j = 0
for j in original_counter:
H_j -= (1.0*original_counter[j] / total_num) * math.log(1.0*original_counter[j] / total_num+eps, 2)
return 2.0 * MI / (H_k + H_j)
sklearn中自带的方法:
from sklearn.metrics.cluster import normalized_mutual_info_score print(normalized_mutual_info_score([0, 0, 1, 1], [0, 0, 1, 1]))
调整互信息AMI( Adjusted mutual information)
已知聚类标签与真实标签,互信息(mutual information)能够测度两种标签排列之间的相关性,同时忽略标签中的排列。有两种不同版本的互信息以供选择,一种是Normalized Mutual Information(NMI),一种是Adjusted Mutual Information(AMI)。
假设U与V是对N个样本标签的分配情况,则两种分布的熵(熵表示的是不确定程度)分别为:
$$H(U)=\sum_{i=1}^{|U|}P(i) \log (P(i))$$
$$H(V)=\sum_{j=1}^{|V|}{P}'(j) \log ({P}'(j))$$
其中:
- $P(i) = \frac{|U_i|}{N}$是从U中随机选取的对象到类$U_i$的概率
- ${P}'(j) = \frac{|V_j|}{N}$从V中随机选取的对象到类$V_j$的概率
U与V之间的互信息(MI)定义为:
$$\text{MI}(U,V) = \sum_{i=1}^{|U|}\sum_{j=1}^{|V|}P(i,j) \log (\frac{P(i,j)}{P(i){P}'(j)})$$
其中$P(i,j) = \frac{|U_i\cap V_j|}{N}$是随机选择的对象落入两个类的概率$U_i$和$V_j$。
调整互信息(Adjusted mutual information)定义为:
$$\text{AMI} = \frac{\text{MI}-E[\text{MI}]}{max(H(U),H(V)-E([\text{MI}]))}$$
MI的期望可以用以下公式来计算。在这个方程式中,$a_i=|U_i|$为$U_i$元素的数量,$b_j=|V_j|$为$V_j$元素的数量:
$$\mathbf{E}\{MI(U, V)\}=\sum_{i=1}^{R} \sum_{j=1}^{C} \sum_{n_{i j}=\max (a_{i}+b_{j}-N, 0)}^{\min (a_{i}, b_{j})} \frac{n_{ij}}{N} \log (\frac{N \cdot n_{ij}}{a_{i} b_{j}}) \frac{a_{i}!b_{j}!(N-a_{i})!(N-b_{j})!}{N!n_{i j} !(a_{i}-n_{i j})!(b_{j}-n_{i j})!(N-a_{i}-b_{j}+n_{i j})!}$$
利用基于互信息的方法来衡量聚类效果需要实际类别信息,MI与NMI取值范围为[0,1],AMI取值范围为[-1,1],它们都是值越大意味着聚类结果与真实情况越吻合。
优点
- 随机(统一)标签分配的AMI评分接近0)
- 有界范围 [0, 1]: 接近 0 的值表示两个主要独立的标签分配,而接近 1 的值表示重要的一致性。此外,正好 0 的值表示 purely(纯粹) 独立标签分配,正好为 1 的 AMI 表示两个标签分配相等(有或者没有 permutation)。
- 对簇的结构没有作出任何假设: 可以用于比较聚类算法
缺点:
- 与 inertia 相反, MI-based measures 需要了解 ground truth classes,而在实践中几乎不可用,或者需要人工标注或手动分配(如在监督学习环境中)。然而,基于 MI-based measures (基于 MI 的测量方式)也可用于纯无人监控的设置,作为可用于聚类模型选择的 Consensus Index (共识索引)的构建块。
- NMI 和 MI 没有调整机会。
from sklearn import metrics labels_true = [0, 0, 0, 1, 1, 1] labels_pred = [0, 0, 1, 1, 2, 2] print(metrics.adjusted_mutual_info_score(labels_true, labels_pred))
Rand index兰德指数
兰德指数 (Rand index, RI), 将聚类看成是一系列的决策过程,即对文档集上所有N(N-1)/2个文档 (documents) 对进行决策。当且仅当两篇文档相似时,我们将它们归入同一簇中。
Positive:
- TP 将两篇相似文档归入一个簇 (同 – 同)
- TN 将两篇不相似的文档归入不同的簇 (不同 – 不同)
Negative:
- FP 将两篇不相似的文档归入同一簇 (不同 – 同)
- FN 将两篇相似的文档归入不同簇 (同- 不同) (worse)
RI 则是计算「正确决策」的比率(精确率, accuracy):
$$RI=\frac{TP+TN}{TP+FP+TF+FN}=\frac{TP+TN}{C_N^2}$$
RI取值范围为[0,1],值越大意味着聚类结果与真实情况越吻合。
def contingency_table(result, label):
total_num = len(label)
TP = TN = FP = FN = 0
for i in range(total_num):
for j in range(i + 1, total_num):
if label[i] == label[j] and result[i] == result[j]:
TP += 1
elif label[i] != label[j] and result[i] != result[j]:
TN += 1
elif label[i] != label[j] and result[i] == result[j]:
FP += 1
elif label[i] == label[j] and result[i] != result[j]:
FN += 1
return (TP, TN, FP, FN)
def rand_index(result, label):
TP, TN, FP, FN = contingency_table(result, label)
return 1.0*(TP + TN)/(TP + FP + FN + TN)
调整兰德系数 (Adjusted Rand index)
对于随机结果,RI并不能保证分数接近零。为了实现“在聚类结果随机产生的情况下,指标应该接近零”,调整兰德系数(Adjusted rand index)被提出,它具有更高的区分度:
$$\mathrm{ARI}=\frac{\mathrm{RI}-E[\mathrm{RI}]}{\max (\mathrm{RI})-E[\mathrm{RI}]}$$
ARI取值范围为[-1,1],值越大意味着聚类结果与真实情况越吻合。从广义的角度来讲,ARI衡量的是两个数据分布的吻合程度。
优点:
- 对任意数量的聚类中心和样本数,随机聚类的ARI都非常接近于0
- 取值在[-1,1]之间,负数代表结果不好,越接近于1越好
- 对簇的结构不需作出任何假设:可以用于比较聚类算法。
缺点:
- 与 inertia 相反,ARI 需要 ground truth classes 的相关知识,ARI需要真实标签,而在实践中几乎不可用,或者需要人工标注者手动分配(如在监督学习环境中)。然而,ARI 还可以在 purely unsupervised setting (纯粹无监督的设置中)作为可用于 聚类模型选择(TODO)的共识索引的构建块。
from sklearn import metrics labels_true = [0, 0, 0, 1, 1, 1] labels_pred = [0, 0, 1, 1, 2, 2] print(metrics.adjusted_rand_score(labels_true, labels_pred))
F值方法
这是基于上述RI方法衍生出的一个方法,我们可以 FN 罚更多,通过取$F_{\beta}$中的$\beta$大于 1, 此时实际上也相当于赋予召回率更大的权重:
$$Precision = P = \frac{TP}{TP+FP}$$
$$Recall = R = \frac{TP}{TP+FN}$$
$$F_{\beta}=\frac{(1+{\beta}^2)P\times R}{{\beta}^2P+R}$$
RI方法有个特点就是把准确率和召回率看得同等重要,事实上有时候我们可能需要某一特性更多一点,这时候就适合F值方法。
def precision(result, label):
TP, TN, FP, FN = contingency_table(result, label)
return 1.0*TP/(TP + FP)
def recall(result, label):
TP, TN, FP, FN = contingency_table(result, label)
return 1.0*TP/(TP + FN)
def F_measure(result, label, beta=1):
prec = precision(result, label)
r = recall(result, label)
return (beta*beta + 1) * prec * r/(beta*beta * prec + r)
Fowlkes-Mallows scores
Fowlkes-Mallows Scores(FMI) FMI是成对的precision(精度)和recall(召回)的几何平均数。取值范围为 [0,1],越接近1越好。定义为:
$$\text{FMI} = \frac{TP}{\sqrt{(TP+FP)(TP+FN)}}$$
代码实现:
from sklearn import metrics labels_true = [0, 0, 0, 1, 1, 1] labels_pred = [0, 0, 1, 1, 2, 2] print(metrics.fowlkes_mallows_score(labels_true, labels_pred))
调和平均V-measure
说V-measure之前要先介绍两个指标:
- 同质性(homogeneity):每个群集只包含单个类的成员。
- 完整性(completeness):给定类的所有成员都分配给同一个群集。
同质性和完整性分数基于以下公式得出:
$$h = 1- \frac{H(C|K)}{H(C)}$$
$$c = 1- \frac{H(K|C)}{H(K)}$$
其中$H(C|K)$是给定给定簇赋值的类的条件熵,由以下公式求得:
$$H(C|K)= -\sum_{c=1}^{|C|}\sum_{k=1}^{|K|} \frac{n_{c,k}}{n} \cdot \log (\frac{n_{c,k}}{n})$$
$H(C)$是类熵,公式为:
$$H(C)= -\sum_{c=1}^{|C|} \frac{n_{c}}{n} \cdot \log (\frac{n_{c}}{n})$$
其中,n是样本总数,$n_c$和$n_k$分别属于类c和类k的样本数,而$n_{c,k}$是从类c划分到类k的样本数量。条件熵H(K|C)和类熵H(K),根据以上公式对称求得。
V-measure是同质性homogeneity和完整性completeness的调和平均数,V-measure取值范围为 [0,1],越大越好,但当样本量较小或聚类数据较多的情况,推荐使用AMI和ARI。公式:
$$v = 2\cdot \frac{h\cdot c}{h+c}$$
代码实现:
from sklearn import metrics labels_true = [0, 0, 0, 1, 1, 1] labels_pred = [0, 0, 1, 1, 2, 2] print(metrics.homogeneity_score(labels_true, labels_pred)) print(metrics.completeness_score(labels_true, labels_pred)) print(metrics.v_measure_score(labels_true, labels_pred))
优点:
- 分数明确:从0到1反应出最差到最优的表现;
- 解释直观:差的调和平均数可以在同质性和完整性方面做定性的分析;
- 对簇结构不作假设:可以比较两种聚类算法如k均值算法和谱聚类算法的结果。
缺点:
- 以前引入的度量在随机标记方面没有规范化,这意味着,根据样本数,集群和先验知识,完全随机标签并不总是产生相同的完整性和均匀性的值,所得调和平均值V-measure也不相同。特别是,随机标记不会产生零分,特别是当簇的数量很大时。
- 当样本数大于一千,聚类数小于10时,可以安全地忽略该问题。对于较小的样本量或更大数量的集群,使用经过调整的指数(如调整兰德指数)更为安全。
- 这些指标要求的先验知识,在实践中几乎不可用或需要手动分配的人作注解者(如在监督学习环境中)。
Jaccard 指数
该指数用于量化两个数据集之间的相似性,该值得范围为0-1.其中越大表明两个数据集越相似:
$$J(A,B) = \frac{|A\cap B|}{|A\cup B|}= \frac{TP}{TP+FP+FN}$$
该指数和近年来的IOU计算方法一致
Dice 指数
该指数是基于jaccard指数上将TP的权重置为2倍。
$$J(A,B) = \frac{|A\cap B|}{|A\cup B|}= \frac{2TP}{2TP+FP+FN}$$